Cartesian Tree

Reading time: 20 minutes | Coding time: 10 minutes

Algorithm

Building the Cartesian tree

Below is linear algorithm to build Cartesian tree following min heap property.

1. Traverse the sequence from left to right.
2. For every node x, repeat steps 3 to 5.
3. Start at the node representing value before x, call it y. Check all nodes in path
    the path from y to root of the tree (including y) until you reach a node with
    value less than x, say z. 
4. If z is found, set the z's right child to be new node, and z's previous child
    to be left child of x.
5. If z is not found, set x to be root and set x's left child to be previous tree.

To create a tree with max heap property, in step 3, search for the first node
    with value greater than x.

The Cartesian tree for the sequence {1, 14, 5, 0, 8} will be:

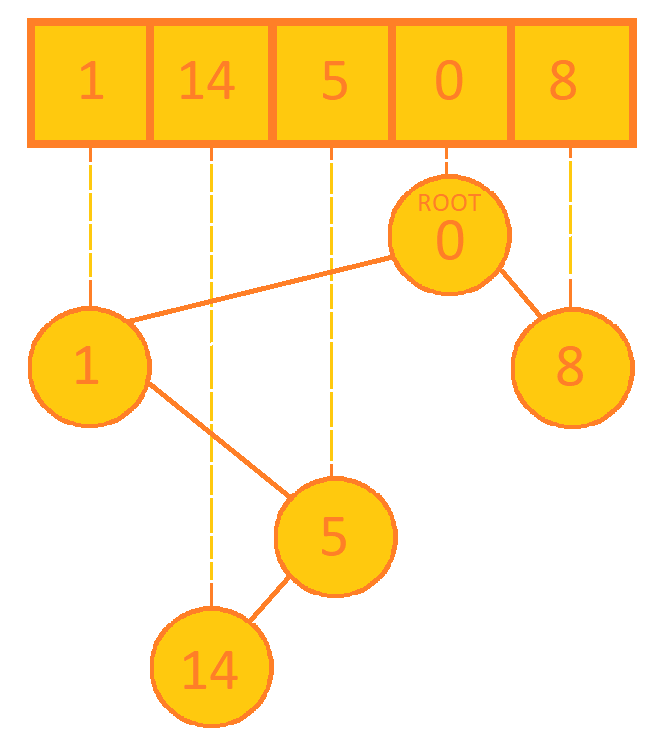
Going from the tree rooted at 0, inorder traversal will give back the original sequence.

Complexity

The time and space complexity of Cartesian Tree are:

$\bf{Space \hspace{1mm }complexity:}\hspace{1mm} O(N)$

$\bf{Time\hspace{1mm }complexities:}$

• $\bf{Build:} \hspace{1mm} O(N)$

Implementations

C++ 11

/* 
 * c++ 11 code to construct a Cartesian tree. The code also contains a fucntion 
 * for inorder traversal of the tree to show that the order is maintained.
 */

#include <iostream>
#include <vector>

struct Node{
    int value;
    Node *left, *right;
    Node *parent;

    Node(){
        value = 0;
        parent = NULL;
        left = NULL;
        right = NULL;
    }
};

class CartesianTree{
private:
    // last pointer to keep track of last node added
    Node *root, *last;

    Node * findLowestNode(Node *node, int x){
        // if(node == NULL)    // i.e. first insertion
        //     return NULL;
        
        if(node->value < x)
            return node;
        else if(node->parent != NULL)
            return findLowestNode(node->parent, x);
        else
            return NULL;
    }

public:
    Node * getRoot(){
        return root;
    }

    void addNode(int x){
        Node *new_node = new Node;
        new_node->value = x;
        if(root == NULL){
            last = new_node;
            root = new_node;
            return;
        }
        Node *z = findLowestNode(last, x);
        if(z == NULL){
            new_node->left = root;
            root->parent = new_node;
            root = new_node;
        }
        else{
            new_node->left = z->right;
            z->right = new_node;
            new_node->parent = z;
        }

        last = new_node;
    }

    CartesianTree(std::vector<int> ar){
        root = NULL;
        last = NULL;
        // Call addNode function for each element of the array
        for(auto x : ar){
            addNode(x);
        }
    }

    void InorderTraversal(Node *node){
        // To print inorder traversal of the tree
        if(node == NULL)
            return;
        InorderTraversal(node->left);
        std::cout << node->value << ' ';
        InorderTraversal(node->right);
    }
};

int main(){
    std::vector<int> ar = {1, 14, 5, 0, 8};
    
    CartesianTree tree(ar);
    tree.InorderTraversal(tree.getRoot());
    std::cout << '\n';
}

Applications

• Cartesian tree sorting is an adaptive sorting algorithm that gives linear time complexity in favourable cases.
• Cartesian tree is used to construct a suffix tree.

References/ Further reading

• Wikipedia article on Cartesian tree
• Try this problem on cartesian tree to solidify your understanding.
• Try building a Cartesian tree with max heap property an an exercise.