Check if 2 Binary Trees are isomorphic

Two Binary Trees are known as isomorphic if one of them can be obtained from the other one by series of flipping of nodes, swapping the children both left and right of number of nodes. Any number of nodes at all levels can swap their child nodes.

With above definition we can say that two empty trees are isomorphic.
Let us consider an example:

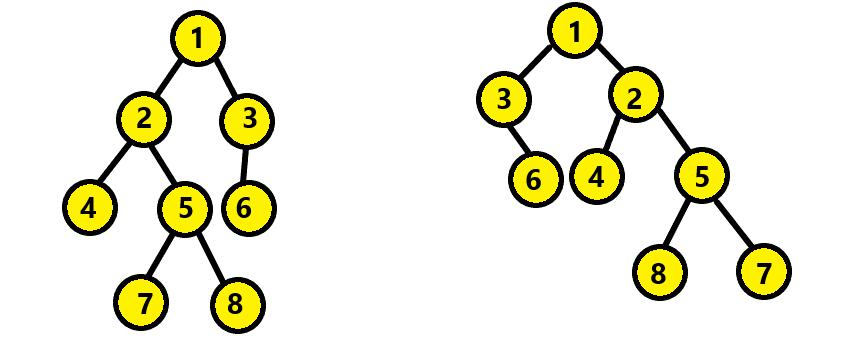
Above trees are isomporhpic.
We can swap node 2 and 3. Then we can swap node NULL and 6. Then finally we can swap node 7 and 8.
We have two main approaches here to follow:

• In approach 1, we need to traverse both trees first.
• In approach 2, we will traverse the trees iteratively using level order traversal and store that in a queue. At each level we will iterate through array to check whether each value exist on map or not.

Definition of a node:

struct node{
    int val;
    struct node*left,*right;
}

Approach 1:

To implement above idea, we need to traverse both trees first. Let current internal nodes of two trees being traversed be n1 and n2

• To be isomorphic we have following conditions:
  • Data of n1 is equivalent to n2
  • One of following is true for children of n1 and n2:
    • Left child of n1 is isomorphic to left child of n2.
    • Right child of n1 is isomorphic to right child of n2
    • Left child of n1 is isomorphic to right child of n2
    • Right child of n1 is isomorphic to left child of n2

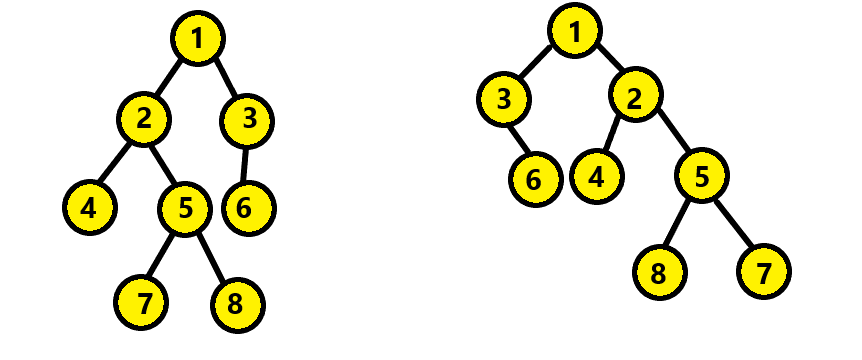
For the above tree, we start by checking if roots of both trees are null. Since roots of both trees are not null hence we check the condition if the value of both root nodes of both trees is equal. Since the value of both root nodes is same hence we return the iterative call of function Isomorphic.
First, We will check the condition if left child of both trees are isomorphic and the right child of nodes of both trees are isomorphic. If any of these conditions holds true then the result will be false since they have && operator.
Second, in "or" operator we called the function again for left and right child of both trees. Using && operator to this condition, we check for right and left child nodes.

Now, the left and right child node of first tree are 2 and 3 respectively. The left and right child node of second tree are 3 and 2 respecitvely.
For the first recursive call, we have left child node of first and second tree. Since both of them have different values. Hence this will result in false.
For the second recursive call we have right child node of first and second tree. They both again have different values. Hence it retruns false.

For the third recursive call, we have left and right child nodes of first and second tree respectively. It returns true.
For the fourth recursive call, we have right and left child nodes of first and second tree respectively. It returns true.

Hence the overall result will be true. In similar fashion we will keep traversing whole tree and find out if it is isomorphic or not.

Function Isomorphic:

• In the function we start by checking if both roots are null or not. If they are null then the trees are isomorphic. Hence we return true if so.
• Then we check if one of n1 and n2 are null then the trees are not isomorphic.
• Then we start to check for both trees being isomorphic if none of above conditions hold true:
  • We start a loop till value of n1 is not equivalent to val of n2
  • We call the Isomorphic function recursively to check :
    • The subtree rooted at these nodes have not been flipped , Both of these subtrees have to be isomorphic
    • The subtrees rooted at these nodes have been flipped

bool Isomorphic(node* n1, node *n2)
{
 if (n1 == NULL && n2 == NULL)
    return true;
 if (n1 == NULL || n2 == NULL)
    return false;
 if (n1->val != n2->val)
    return false;
 return 
 (Isomorphic(n1->left,n2->left) && Isomorphic(n1->right,n2->right))|| Isomorphic(n1->left,n2->right) 
 && Isomorphic(n1->right,n2->left));
}

This solution will take Time Complexity of O(min(x,y) * 2) or O(min(x,y)) where x and y represents the number of nodes in given trees.

Approach 2:

We will traverse the trees iteratively using level order traversal and store that in a queue.The conditions to be checked are:
- The values of nodes is same
- The number of nodes at each level is same
We have to check the size of queue to ensure that the second condition is true. We will store the nodes of each level of first tree as val. For second tree store the nodes of the tree in vector. In case of repetitive values, we will decrease the value to keep track of how many nodes with same value exist at given level. If value become zero then it shows that the first tree only has this much number of nodes. At each level we will iterate through array to check whether each value exist on map or not. There are 3 key conditions:

1. If the key is not found then first tree does not have node found in other tree does not have node at given level
2. If key is found but value is negative then second tree has more nodes with same value as first one
3. If size of the map is not zero then it means there are some keys left. Hence the first tree has node that does not match any node in other tree

Function Isomorphic:

• We check if both roots are null then the tree is isomorphic
• Else we check if one node is false
• Then we start to enqueue the roots of both trees if above conditions are false
• Then we start a while loop till either queue is empty
  • We check if number of nodes are not same at given level
  • Then in another loop we dequeue the nodes
  • We check if the value exists in the map
  • Then we enqueue the child nodes
• Then we iterate through each node to check if it exists. We do this at each level
• Finally we check if there is any key remaining then we return false
• Else return true

bool Isomorphic(node* root1, node* root2)
{
    if (root1 == NULL and root2 == NULL)
        return true;
    else if (root1 == NULL or root2 == NULL)
        return false;
        queue<node *> q1, q2;
    q1.push(root1);
    q2.push(root2);
    int level = 0,size;
    vector<int> v2;
    unordered_map<int, int> mp;
    while (!q1.empty() && !q2.empty()) {
        if (q1.size() != q2.size())
            return false;
        size = q1.size();
        level++;
        v2.clear();
        mp.clear();
        while (size--) {
            node* temp1 = q1.front();
            node* temp2 = q2.front();
            q1.pop();
            q2.pop();
            if (mp.find(temp1->data) == mp.end())
                mp[temp1->data] = 1;
            else
                mp[temp1->data]++;
            v2.push_back(temp2->data);
            if (temp1->left)
                q1.push(temp1->left);
            if (temp1->right)
                q1.push(temp1->right);
            if (temp2->left)
                q2.push(temp2->left);
 
            if (temp2->right)
                q2.push(temp2->right);
        }
        for (auto i : v2) {
            if (mp.find(i) == mp.end())
                return false;
            else {
                mp[i]--;
                if (mp[i] < 0)
                    return false;
                else if (mp[i] == 0)
                    mp.erase(i);
            }
        }
        if (mp.size() != 0)
            return false;
    }
    return true;
}

In the first approach we will check the conditions mentioned above taking Time Complexity of O(min(x,y) * 2) or O(min(x,y)) where x and y represents the number of nodes in given trees.

In second approach we will traverse the trees iteratively using level order traversal and store that in a queue. Then we will check the above mentioned conditions. Hence, using above approaches we can check if the two binary trees are isomorphic or not.