
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
To convert binary tree to circular doubly linked list, we will take left node as previous pointer and right node as next pointer. The order of nodes in Doubly Linked List must be same as in inorder of the given binary tree. The very first node of inorder traversal will become the head of the doubly linked list.
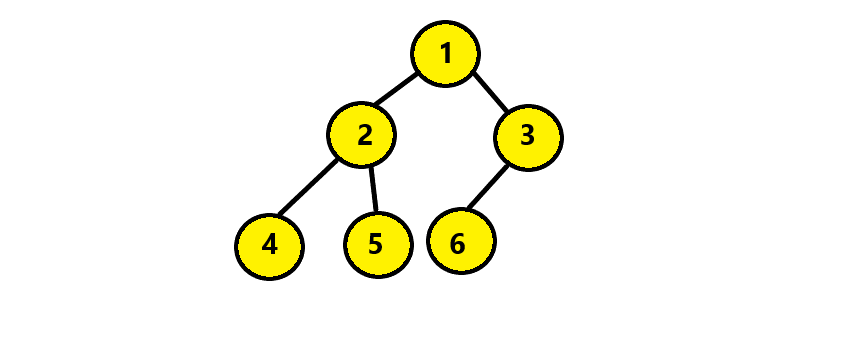
In the above binary tree, we will get the doubly linked list as follows:

We need to check following conditions:
- If left subtree exists then process left subtree to DLL. We will use recursion to convert left subtree to DLL. Then we will find inorder predecessor (left most node in left subtree) of root in left subtree. Then we will make inorder predecessor as previous of root.
- If right subtree exists then we follow below conditions to process it. Recursively convert right subtree to DLL. Find inorder successor of root in right subtree. Make inorder successor as next of root. Make root as previous of inorder successor. Find leftmost node and return that as head of dll.
We have two main approaches:
- In first approaches we will use two functions, first is function convert. We will use inorder traversal to convert the binary tree. We will form the doubly linked list by using convert function.
- In next approach, we will traverse the tree in inorder fashion. Then we will keep track of each node we visit.
Definition of node in Binary Tree
struct node{
int val;
node * left,*right;
}
Approach 1
In this approach we will use two functions, first is function convert. In convert function we will use inorder traversal to convert the binary tree. In next function, dll we will form the doubly linked list by using convert function.
Function convert:
- In this we first check if the nodes are null or not.
- Then we convert the left subtree and link it to the root. Then we will convert the left subtree.
- Then we will find the inorder predecessor. After this loop, left points to the inorder predecessor.
- Make root as next of predecessor and predecessor as previous of root.
- Then we convert right subtree and link it to the root.
- Then we will convert the right subtree.
- Then we will find the inorder successor. After the loop, right will point to the inorder successor.
- Make root as previous of successor.
- Make successor as next of root.
node* convert(node* root)
{
if (root == NULL)
return root;
if (root->left != NULL) {
node* left = bintree2listUtil(root->left);
for (; left->right != NULL; left = left->right);
left->right = root;
root->left = left;
}
if (root->right != NULL) {
node* right = bintree2listUtil(root->right);
for (; right->left != NULL; right = right->left);
right->left = root;
root->right = right;
}
return root;
}
Function dll:
- First we check for the base case. If the root is null then we return root.
- Else, then we call convert function above. It returns the root node of converted DLL.
- We will need pointer to left most node as it will be the head for the DLL. Now we start a while loop to return left most node.
- In the end we return root.
node* dll(node* root)
{ if (root == NULL)
return root;
root = convert(root);
while (root->left != NULL)
root = root->left;
return (root);
}
Approach 2:
In this approach we will traverse the tree in inorder fashion. Then we will keep track of each node we visit. We will keep track of the DLL head and tail pointers, insert each visited node at end of DLL using tail ptr. Finally we return the head of the list.
node* convert(node* root, node** head, node** tail)
{
if (root == NULL)
return NULL;
node* left = root->left;
node* right = root->right;
convert(root->left, head, tail);
if (*head == NULL) {
*head = root;
}
root->left = *tail;
if (*tail != NULL) {
(*tail)->right = root;
}
*tail = root;
convert(root->right, head, tail);
return root;
}
Function dll:
- Firstly, we check if the root is null. If so then we return null.
- Else we initialise head and tail pointers as null.
- Then we call convert function.
- In the end we return head.
node* dll(node* root)
{
if (root == NULL)
return root;
node* head = NULL;
node* tail = NULL;
convert(root, &head, &tail);
return head;
}
Approach 3:
In this approach have two types of pointers:
- Fixed Left pointers: We will fix the left pointer. We will change left pointers to point to previous nodes in DLL. We will perform inorder traversal of the tree. In inorder traversal we will keep track of previous visited nodes. We will change left pointer to previous node.
- Fixed left pointers: We will use the left pointers fixed as above. Starting from rightmost node in Binary Tree, it is the last node in DLL. Since left pointers are changed to point to previous node in DLL. Hence, we can traverse the complete DLL using these pointers. The traversal is from last to first node. While traversing we will keep track of previously visited node. We will change right pointer to previous node.
We have four main functions. In function Inorder we will do inorder traversal of binary tree. In function prev, we change left pointers to work as previous pointers. The function is performing inorder traversal. In function next, we change right pointers to act as next pointers in converted DLL. In function fin, we convert the binary tree to DLL.
Time Complexity : O(n)
Function Inorder:
- This function implements the inorder traversal.
- First we check if the root is not null. Then we recursively call this function for left subtree.
- Then recursively we call this function for right subtree.
void inorder(node *root)
{
if (root != NULL)
{
inorder(root->left);
cout << root->data;
inorder(root->right);
}
}
Function prev:
- In this function, we change left pointers to work as previous pointers.
- The function is performing inorder traversal.
- Then it updates left pointer using previously visited node.
void prev(node *root)
{
static node *pre = NULL;
if (root != NULL)
{
prev(root->left);
root->left = pre;
pre = root;
prev(root->right);
}
}
Function next:
- In this function, we change right pointers to act as next pointers in converted DLL
- We find the right most node in binary tree or last node in DLL
- We start from the rightmost node, traverse using left pointers.
- While traversing we change right pointer of nodes
- The leftmost node is the head of the linked list. We will return it.
node *next(node *root)
{
node *prev = NULL;
while (root && root->right != NULL)
root = root->right;
while (root && root->left != NULL)
{
prev = root;
root = root->left;
root->right = prev;
}
return (root);
}
Function fin:
- In this function, we convert the binary tree to DLL.
- We first set previous pointer.
- Then we set next pointer and return head of DLL
- Then we traverse the DLL from left to right
node *fin(node *root)
{
prev(root);
return next(root);
}
void printList(node *root)
{
while (root != NULL)
{
cout<<root->data;
root = root->right;
}
}
Approach 4:
It is the most optimal approach. Time Complexity is O(n). In this approach, we will do inorder traversal of binary tree. While inorder traversal we will keep track of the previously visited nodes in prev variable. For each node that has been visited we make it next of prev and previous of this node as prev. Instead of static used in below implementation we can also use double pointer or refernce pointer.
For example consider the below tree:
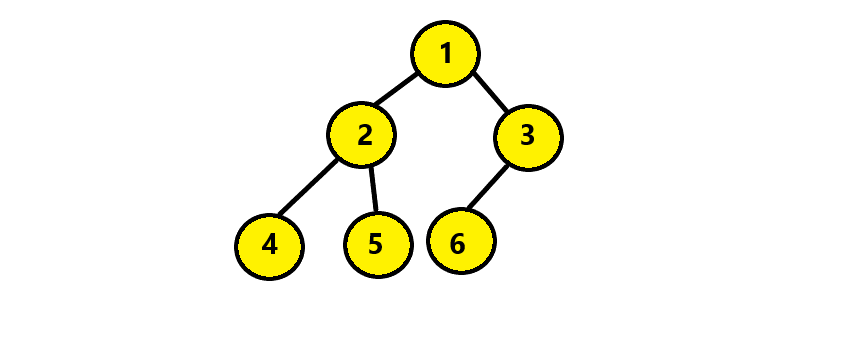
We start by checking if the root is null. Since this is not the case hence we move to next condition. We initialise prev with NULL. Then we call convert function recursively for the left subtree of the root, starting from node 2. Then again we would call left child of node 2, that is node 4. Then the node 4 will have no left child, hence we will return. Then since the prev will be NULL hence we initialise head with root, that is node 4. Prev will be set to node 4 that is root for this call. Then node 4 does not have right child node either. Hence we return and now the root is node 2.
Now left of root will be prev that is node 4 and right of prev will be root that is node 2. Now the prev will be node 2. Then we will call the convert function for left subtree with root node 2.
In the same fashion we will keep making recursive calls and hence our doubly linked list would be formed in the end.
Function convert:
- We start by checking if the root is null. If so then we retrun.
- Else Initialise the previously visited node as NULL.
- We have taken it static for accessibility of same value in all recusive calls.
- Then we recusively convert the left subtree
- Then we convert the node
- Then we convert the right subtree.
void convert(node *root, node **head)
{
if (root == NULL) return;
static node* prev = NULL;
convert(root->left, head);
if (prev == NULL)
*head = root;
else
{
root->left = prev;
prev->right = root;
}
prev = root;
convert(root->right, head);
}
Hence, using above approaches we can easily convert Binary Tree to Circular Doubly Linked list. We can either use inorder traversal as mentioned in approach 1 and 2. We can also use optimal approach consuming O(n) time complexity by using two fixed pointers. It will also use inorder traversal.
At the end we have the most optimal, approach 4 using O(n) with inorder traversal. Instead of static used in below implementation we can also use double pointer or refernce pointer.
