Succinct (0-1) Encoding of Binary Tree

Succinct encoding is an approach to encode a Binary Tree to the lowest possible space and maintain the structural information. The number of structurally different binary trees on n nodes is nth Catalan's Number. Catalan numbers are a sequence of natural numbers that occur in various problems like counting the possible Binary Search trees with n values, counting the number of binary trees with n+1 leaves etc. Some Catalan numbers for n = 0, 1, 2, 3 ... are 1, 1, 2, 5 ...
They can be found using following formula:

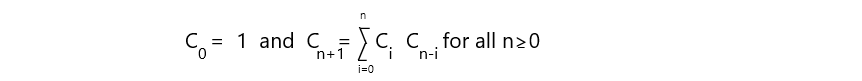
For large n, it becomes equiavalent to 4 raised to power n. Hence we need atleast log base 2 ( 4 raised to power n) bits to encode that. It is equivalent to 2n. On the whole, a succinct tree would occupy 2n + O(n) bits to encode.

To implement this encoding we can first traverse the nodes of the tree in preorder traversal. This should output the encoding of "1" for internal node and "0" for leaf nodes. In case of the tree nodes containing values, we can store them in an array using preorder traversal.

Example:
For the below given tree,

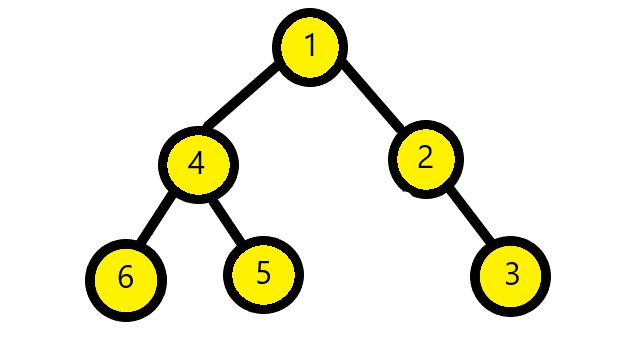
We will check if the node is null. Since the root node is not null then we append value of binary tree to data array and 1 to s.
Then we go to left subtree. So, after root node we check node 4. Since it is not null hence we put 1 in encoding. Then we check its left subtree. Node 6 is not null hence we put 1 in encoding. Then the left subtree of 6 is null hence we put 0. Then we check the right subtree of 6, which is null hence we again put 0. Then we go back to node 4 and check right subtree of node 4. Node 5 is not null hence we insert 1. Then the left and right subtree of 5 is null hence we put 0. Then we return to node 4 then to node 1. The left subtree of node 1 is traversed then we traverse the right subtree of node 1. Here the right subtree of node 1 is node 2. Hence we insert 1. for the left subtree of node 2 we insert 0 and for the right subtree we have node 3. For the node 3 we have both right and left subtree as null hence we insert 0.
We kept on inserting the values of nodes in data array continuously.

We will have following encoding:
1 1 1 0 0 1 0 0 1 0 1 0 0
where 1 stands for data and 0 for NULL values.

Following the above algorithm we can implement this problem as follows:

A binary tree node definition:

struct node{
    int val;
    struct node * left, *right;
}

Algorithm for encoding

• We start by checking if the node is null or not.
• If it is null then we will append 0 to s.
• Else we append 1 to s.
• Then we append value of node to data array at nth index.
• Then we recursively call encoding function for left subtree and then for right subtree.

function encoding(node n, bitstring s, array data){
    if(n == NULL){
        append 0 to s;
    }
    else{
        append 1 to s;
        append n.data to data;
        encoding(n.left, s, data);
        encoding(n.right, s, data);
    }
}

function encoding:

void encoding(node *root, list<bool> &s, list<int> data){
    if(root==0){
        s.push_back(0);
        return;
    }
    else{
        s.push_back(1);
        data.push_back(root->val);
        encoding(root->left,s,data);
        encoding(root->right,s,data);
    }
}

Algorithm for decoding:

• We start by appending first bit of s to x and remove it from s
• If x is equivalent to 1 then we create new node n
  • Then we remove first element of data and put in n.data
  • We call recursively decoding function for left node and then for right node.
  • Then we return n node.
• Else we return NULL

Example:
We have the following encoding given to us: 1 1 1 0 0 1 0 0 1 0 1 0 0

For the decoding, since the first value is 1 hence we create new node. The first element of data array be put in the val of the node. Hence, we obtain our root node with value 1. We follow this fashion for left nodes and then for right nodes. Then in the end we return node n and our tree is obtained. Else in the case of null node we would return null.

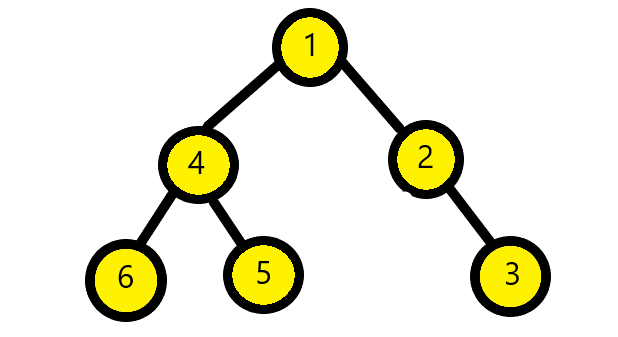
Then after the decoding we will get back our binary tree as below:

function decoding(bitstring s, array data){
    append first bit of s to x and remove it
    if(x==1){
        create new node n
        remove first element of data and put in n.data
        n.left = decoding(s, data)
        n.right = decoding(s,data)
        return n
    else{
        return null
    }
    }
}

function for decoding:

node *decoding(list<bool> &s, list<int> &data){
    if(s.size()==0)
        return NULL;
    else{
        bool b = s.front();
        s.pop_front();
        if(b==1){
            int val = data.front();
            data.pop_front();
            node *root=newnode(val);
            root->left = decoding(s,data);
            root->right = decoding(s,data);
            return root;
        }
    return NULL;
    }
}

With the help of above functions, we can easily do succint encoding and decoding of the binary tree. We can use recusion for encoding and decoding of the tree as expalined in above approaches.