
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this problem, we will find the Lowest Common Ancestor of a Binary Tree using Euler tour and Range Minimum Query. We can solve the LCA problem by reducing it to a RMQ problem. There are many approaches to find the LCA of nodes but have different space and time complexities. This is the most efficient approach.
Range Minimum Query is used on arrays to find the position of an element with minimum value between two specified indices. There are many approaches to implement Range Minimum Query methods.
Euler tour technique (ETT) is named after Leonhard Euler. It is the graph theory for representing trees. The tree is viewed as a directed graph with two directed edges. We can construct it from the given undirected edges. First, construct symmetric list of direct edges. Then sort the edge list lexicographically. Then, we can construct adjacency lists for each node. Also, construct a map from nodes to the first entries of the adjacency lists.
We can also find LCA without using RMQ algorithm, as discussed here. But we can find more optimised solution using the RMQ algorithm/ Euler's Tour.
Euler Tour Method
- Processing Time : O(n)
- Query Time using Range Minimum Query with Segment Tree : O(log N)
- Query Time with naive approach: O(N)
- Extra Space : O(n)
Using RMQ with Segment Tree is efficient, when we want to answer multiple queries.
Query is to find LCA of two nodes that is minimum element in a range.
When we use Euler's Tour method to find LCA then we traverse the whole tree starting from the root using the Euler Tour method. In this method, we use DFS traversal with preorder traversal characteristics.
Introduction
Segment Trees:
A segment tree is also known as a statistic tree. It is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. Indeed it is a very flexible data structure and many different types of problems can be solved using it.
RMQ:
It solves the problem of finding the minimum value in a given subarray from an array of objects thant can be compared. This algorithm is used for solving various problems like Lowest Common Ancestor and Lowest Common Prefix Problem.
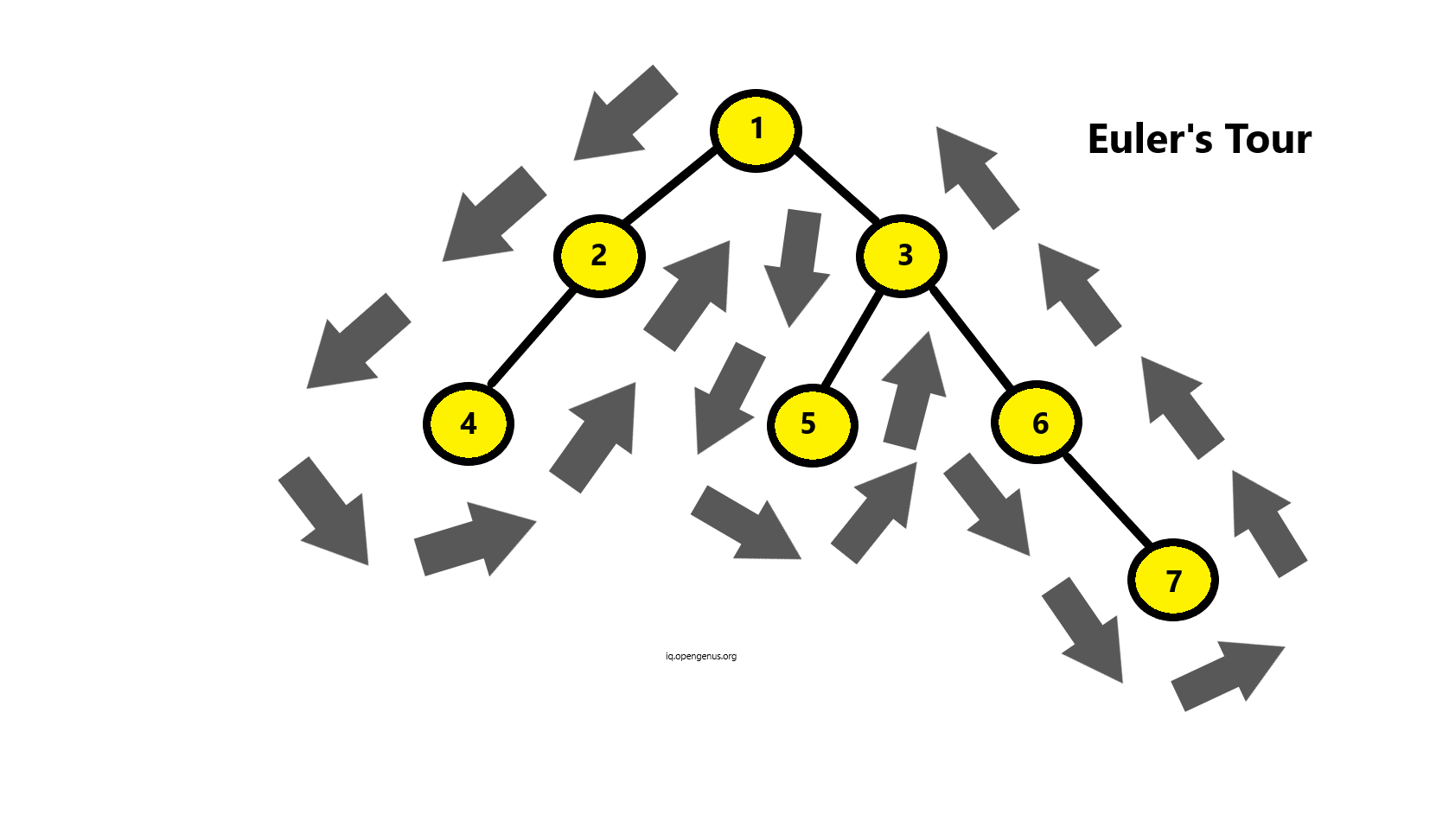
The LCA of the nodes 5 and 7 is 3. We can get this answer from the above euler's path as well. Node 3 is also the closest of all nodes encountered between 5 to 7 node during the Euler's Tour. To implement this we require :
- Array to store Nodes that we visit during the Euler's Tour
- Array to store Each node's respective levels
- Array to store Indexing of first occurence of all nodes
Assumptions:
- All nodes that have been queried have been already present in the tree
- The values of all nodes is between 1 and total number of nodes
Time Complexity:
- Euler's Tour follows depth first approach, therefore for a tree of total nodes "x", DFS will take O(x + (x-1)) which will become O(2x) which further becomes O(x).
- Segment Tree will take O(n) where n will be equivalent to (2 * x) -1
- Range Minimum Query algorithm will take O(log(n))
- Hence, this method will take O(n) time for the processing and O(log(n)) for the RMQ. This method is very efficient in case when we have a single tree on which we will perform many LCA queries.
Auxillary Space:
- Euler's Tour Array will take O(n)
- Level Array will take O(n)
- First Occurences Array will take O(x)
- Segment Tree will take O(n)
- Overall it will take O(n)
If we put the Euler's Tour into tabular form, it would be as follows:
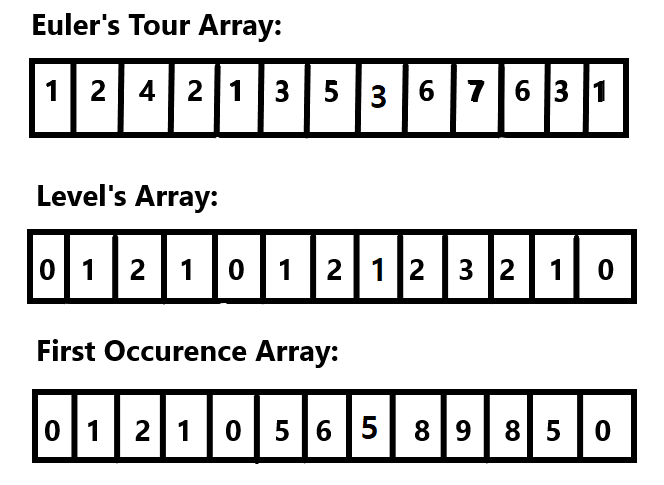
Euler's Tour Array:
- When we have to fill Euler's Tour Array, then we start from root node 1. Then we move to next node as arrows follow.
- We move to node 2. Then we move to node 4.
- Now, we again turn to node 2 from node 4, since we are iterating the tree using Euler's Tour method.
- In the similar fashion we keep on iterating the tree according to the arrows.
Level's Array:
- With respect to the Euler's Tour Array, in this array we have to fill the respective levels of the nodes visited in Euler's Tour array.
- Starting from the first value in Level's array, it corresponds to the level of the first value in Euler's array.
- The first value in Euler's array was on level 0. Then node 2 from Euler's array is at level 1, hence value 1 at second index of level's array. In this fashion we will fill the level's array.
First Occurence Array:
- In this array we consider Euler's array and put values of levels where the node occured for the first time.
- For example, node 1 in Euler's array occured at level 0. Hence value 0 in first index of first occurence array. Then node 2 of euler's array occured for the first time at level 1 hence second index of first occurence has value 1.
- Similar fashion is followed and hence we formed the first occurence array.
Example:
Following are the 3 arrays for our sample Binary Tree:
For example:
We want to find the LCA for node 5 and node 7.
From the level array, we see that level of node 5 is 2 and level of node 7 is 3.
From the first Occurence array, we see that first Occurence of node 5 is 6 and node 7 is 9.
Hence, we need to consider the range of index 6 to 9 and all elements with level less than the level of node 5 and 7 is an ancestor. The element with the maximum level that is less than the level of node 5 and 7 is the Lowest Common Ancestor (LCA).
The elements in the range are: 5, 3, 6, 7 with level 2, 1, 2, 3
Hence, the answer is node 3.
Procedure
The algorithmic steps are:
- Perform Euler's Tour on the tree provided
- Enter values in three arrays:
- Euler's Array
- Level Array
- First Occurence Array
- We will get indices of given two nodes from the first occurence array. It will be corners of the range in level array which will be used for our Range Minimum Query Algorithm.
- The element in the range in level array with the lowest level is our answer. For this, we can use RMQ if we want to find LCA of multiple nodes.
- The algorithm will return the minimum level in the range. It will be used to determine Lowest Common Ancestor using the Euler Tour Array.
All the adjacent elements in level array will differ by 1. Hence, these problems can be easily converted from Range Minimum Query Problem to Lowest Common Ancestor Problem.
Binary Tree Node:
struct node
{
int val;
struct node *left, *right;
};
Log Base 2 of x
int Log2(int x)
{
int ans = 0 ;
while (x>>=1) ans++;
return ans ;
}
Function LCA
- This function returns the LCA of nodes n1 and n2 since we have made an assumption that the nodes are already present in the tree
- Then we mark the unvisited nodes. Here the size of first occurence is 1 as node values varying from 1 - 9 are used as indexes
- We have used the memset function. It converts the value ch to unsigned char and copies it into each of the first n characters of the object pointed to by pointer to the object to copy the character
- Then we start to fill level and euler arrays from 0 index
- We start the function Euler from level 0 of root node
- Then we construct the segment tree on our level array
- For our Range Minimum Query Algorithm, u must be smaller than v.
- Then we define the starting and ending indexes of query range
- Then we create query for index of LCA in tour
- Then we return the LCA node
int LCA(node *root, int u, int v)
{
memset(firstOccurrence, -1, sizeof(int)*(V+1));
ind = 0;
Euler(root, 0);
int *st = segmentaux(level, 2*V-1);
if (firstOccurrence[u]>firstOccurrence[v])
std::swap(u, v);
int qstart = firstOccurrence[u];
int qend= firstOccurrence[v];
int index = RMQ(st, 2*V-1, qstart, qend);
return euler[index];
}
Calculate Euler tour: Function Euler
- This is the recursive function for the Euler Tour of our tree
- It starts by checking if the root is not null and it exists
- If the root exists then insert it into the euler array
- Then we insert 1 in level array
- Then we increment the index
- If the index of first occurence array is unvisited then we mark first occurence
- Then we again traverse the left subtree if it exists and mark our euler array again along with level arrays for parents on return
- Now, tour the right subtree if it exists and mark euler array and level array for parents on return
void Euler(node *root, int l)
{
if (root)
{
euler[ind] = root->val;
level[ind] = l;
ind++;
if (firstOccurrence[root->val] == -1)
firstOccurrence[root->val] = ind-1;
if (root->left)
{
Euler(root->left, l+1);
euler[ind]=root->val;
level[ind] = l;
ind++;
}
if (root->right)
{
Euler(root->right, l+1);
euler[ind]=root->val;
level[ind] = l;
ind++;
}
}
}
Calculating Range Minimum Query using Segment Tree
RMQaux Function:
-
This function is a recursive function that will help us get the minimum value in a given range of array indexes. The arguments are:
- index : It represents the index of the current node in segment tree. Initially the index is set at 0 since the root node is passed
- st : It is the pointer to the segment tree
- start and end: It represents the starting and ending indexes of the segment represented by current node
- qstart and qend : They represent the query range starting and ending indexes
-
Firstly we check if segment of this node is a part of given range, then return the min of the segment
-
If segment of this node is outside the given range then we return -1
-
Then we check if a part of this segment overlaps with the given range. We calculate the mid value of start and end of segment represented by node. Then we have two variables q1 and q2 which store the result of recursively called RMQaux function.
- If q1 is equivalent to -1 then we return q2
- If q2 is equivalent to -1 we return q1
- else return q1 if level at q1 is smaller else return q2
int RMQaux(int index, int start, int end, int qstart, int qend, int *st)
{
if (qstart <= start && qend >= end)
return st[index];
else if (end < qstart || start > qend)
return -1;
int mid = (start + end)/2;
int q1 = RMQaux(2*index+1, start, mid, qstart, qend, st);
int q2 = RMQaux(2*index+2, mid+1, send, qstart, qend, st);
if (q1==-1) return q2;
else if (q2==-1) return q1;
return (level[q1] < level[q2]) ? q1 : q2;
}
Function RMQ
- This function returns the minimum of elements in the range from index query start "qstart" till ending "qend".
- It calls the RMQaux function defined above.
int RMQ(int *st, int n, int qstart, int qend)
{
if (qstart < 0 || qend > n-1 || qstart > qend)
{
printf("Invalid Input");
return -1;
}
return RMQaux(0, 0, n-1, qstart, qend, st);
}
Function segment
- This function is used to construct the segment tree for given array where start and end represent the starting and ending indexes of the segment represented by current node.
- If there is one element in array then we store it in the current node of the segment tree and return
- Else we recursively call the left and right subtree and store the minimum value out of the two in this node
void segment(int si, int start, int end, int arr[], int *st)
{
if (start == end)
st[si] = start;
else {
int mid = (start + end)/2;
segment(si*2+1, start,mid, arr, st);
segment(si*2+2, mid+1,end, arr, st);
if (arr[st[2*si+1]] < arr[st[2*si+2]])
st[si] = st[2*si+1];
else
st[si] = st[2*si+2];
}
}
Function segmentaux
- This function will be used to construct the segment tree from the array.
- This function will allocate the memory for the segment tree and will call the segment function to fill that memory.
- Firstly, in the function we allocate memory using the height of segment tree. For calculation of height we use the Log2 function defined above.
- Then we define the maximum possible size of the tree.
- Then we fill the allocated memory using the segment function defined above
- Finally we return the constructed segment tree
int *segmentaux(int arr[], int n)
{
int x = Log2(n)+1;
int max_size = 2*(1<<x) - 1;
int *st = new int[max_size];
segment(0, 0, n-1, arr, st);
return st;
}
Using above methods we can easily implement the LCA in Binary Tree using Euler tour/ Range Minimum Query.
