
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In binary trees, for given two nodes a and b, the lowest common ancestor is the node of which both a and b are descendants. Here a node can be descendant of itself.
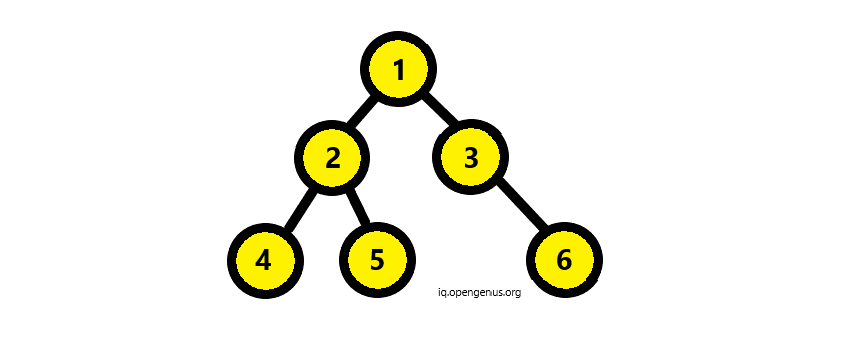
In the above image, if we consider two nodes 2 and 3 then their lowest common ancestor will be node 1.
Similarly, the lowest common ancestor of 4 and 5 will be 2 and that of 3 and 4 would be 1.
The lowest common ancestor is the common and shared descendant of both given nodes.
LCA is used in many other binary tree problems like in determining the distance between pairs of nodes in a tree.
We can find the LCA in many ways as below:
- Procedure 1: 2 traversals
- Proceduce 2: 1 traversal
Procedure 1
Algorithmic steps to find Lowest Common Ancestor in a Binary Tree are:
- Traverse and store the path from the root node till given first node.
- Traverse and store the path from the root node till given second node.
- Traverse both stored paths and return the common node. It will be their LCA.
Time complexity O(n)
Below is the definition of a node:
//definition of a node
struct node{
public:
int val;
node* left;
node* right;
};
The find function:
- If the root is null then we return false.
- Else we push the node of the path of given node to the path vector.
- If value of root is same as given node k then return true.
- If either of two conditions return true then we return true:
- Left of root and recursive call of find function with arguments left of root, path and k return true. It checks if the k is found in the left subtree.
- Right of root and recursive call of find function with arguments right of root, path and k return true. It checks if the k is found in right subtree.
- If the given node we have been searching for is not present in the tree then we delete the root from our vector path and return false.
bool find(node *root, vector<int> &path, int k)
{
if (root == NULL) return false;
path.push_back(root->val);
if (root->val == k)
return true;
if ( (root->left && find(root->left, path, k)) || (root->right && find(root->right, path, k)) )
return true;
path.pop_back();
return false;
}
The above function will be used to find the path of both given nodes. We will start the traversal from the root of the tree and keep traversing recursively till we find given node or we reach the leaf node.
The LCA function:
- Firstly we initialise the integer vectors path1 and path2.
- Then If either of two conditions return false then we return -1:
- We call function find defined above with arguments root, path1 and given node a. If this returns false then it means that the node a was not found in the tree.
- We call function find defined above with arguments root, path2 and given node b. If this returns false then it means that the node b was not found in the tree.
- Now we initialise integer i.
- In the for loop we iterate till either of path1 or path2 vectors ends. If we get any different value that means its previous node was the least common ancestor.
- Hence we return the node at i-1 address of path1 vector.
int LCA(node *root, int a, int b)
{
vector<int> path1, path2;
if ( !find(root, path1, a) || !find(root, path2, b))
return -1;
int i;
for (i = 0; i < path1.size() && i < path2.size() ; i++)
if (path1[i] != path2[i])
break;
return path1[i-1];
}
We will use the above function to find the least common ancestor after the paths of both given nodes have been traversed and stored.
Procedure 2
- In this method we assume that the nodes already exist in the tree.
- If we do so then there will be no need to store the paths of both given nodes and we can traverse and find the LCA of nodes without any storage of path.
- We start from the root of the tree. If any of the given nodes is the root then it is the LCA.
- We recusively traverse the right and the left subtree.
- If both given nodes lie in left and right subtrees of any third node say x, then x will be the LCA.
- If both nodes lie in either left subtree then the LCA will also be found in the left subtree. Similarly if both nodes lie in right subtree then LCA will be in right subtree.
Time Complexity O(N)
Function find:
- This function returns pointer to LCA of two given values n1 and n2.
- Firstly, we check if the root is null. If so then we return false.
- Then we check if the value of root is equivalent to n1 then we set v1 to true and return root.
- If the value of root is equivalent to n2 then we set v2 to true and return root as LCA.
- Then we recursively call LCA function for left subtree of root and then for right subtree.
- If both recurive calls return true then we will return the root.
- Else we check, if left_lca is not null then we return it else we return right_lca.
struct node *find(struct node* root, int n1, int n2, bool &v1, bool &v2)
{
if (root == NULL) return NULL;
if (root->key == n1)
{
v1 = true;
return root;
}
if (root->key == n2)
{
v2 = true;
return root;
}
node *left_lca = find(root->left, n1, n2, v1, v2);
node *right_lca = find(root->right, n1, n2, v1, v2);
if (left_lca && right_lca) return root;
return (left_lca != NULL)? left_lca: right_lca;
}
Function present:
- This function returns true if key k is present in tree rooted with root.
- Firstly, we check if the root is null. If so then we return false.
- If either of the condition is true then we return true:
- If value of root is equivalent to k
- If recursive call for the left subtree of root returns true
- If recursive call for the right subtree of root returns true
- Else we return false.
bool present(node *root, int k)
{
if (root == NULL)
return false;
if (root->val == k || present(root->left, k) || present(root->right, k))
return true;
return false;
}
Function LCA:
- If both n1 and n2 are present in the tree then this function will return the LCA else retrun null.
- Firstly, we initialise the boolean v1 and v2 as false.
- Then we call function find we defined above and pass root, n1, n2, v1 and v2. We store its result in lca pointer of type node.
- If any of the following conditions is true then we return lca:
- v1 and v2 are both true
- v1 and result of recursive call to present function with arguments lca and n2 returns true
- v2 and result of recursive call to present function with arguments lca and n1 returns true
- Else we return null
node *LCA(node *root, int n1, int n2)
{
bool v1 = false, v2 = false;
node *lca = find(root, n1, n2, v1, v2);
if (v1 && v2 || v1 && present(lca, n2) || v2 && present(lca, n1))
return lca;
return NULL;
}
Using above methods we can find the Lowest Common Ancestor for any set of nodes in binary tree. The ideas involved the important to solve several related problems.
