
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
There are three main operations which can be done on a threaded binary tree:
- Insert
- Search
- Delete
In these operations I'm using a doubly threaded binary tree let's look at them one by one:
Insert in Threaded Binary Tree
If we want to insert new node in threaded binary tree then we can use insert operation.
To insert any node in threaded binary tree three cases might arise
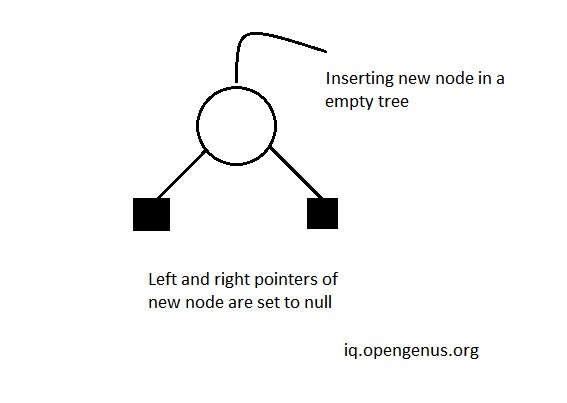
1.When new node is inserted in a empty tree.
2.When new node is inserted as left child of some node in the tree.
3.When new node is inserted as right child of some node in the tree.
Case 1
when new node is inserted in a empty threaded binary search tree we set it's left and right pointers as null pointers , this step is same in both binary as well as threaded binary search tree.
root = tmp;
tmp -> left = NULL;
tmp -> right = NULL;
Case 2
When new node is inserted in binary search tree as left child of some already existing node then node we perform two operations in struct of parent and two operations in struct of child for example -
For Child
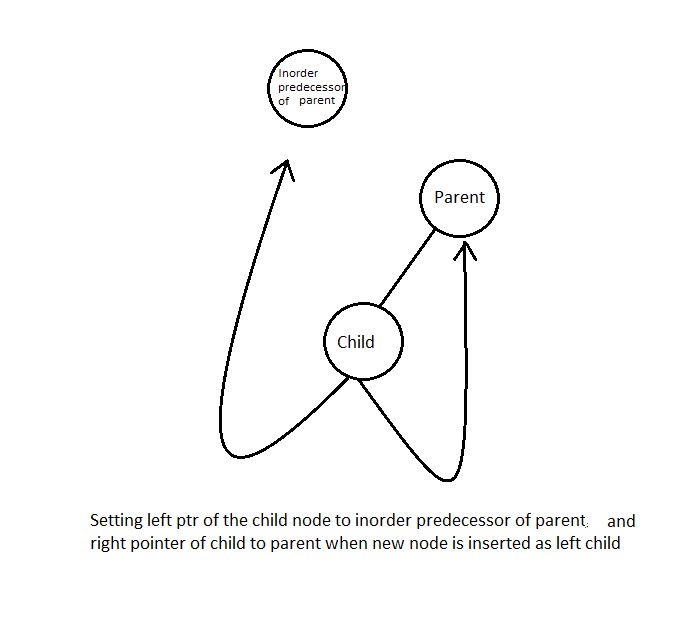
for newly inserted child node (temp here ) we set it's left point to left of parent and it's right point to parent.
tmp -> left = par ->left;
tmp -> right = par;
For Parent
For parent of the child node inserted we set it's lthread to true indicating left child exist and also setting it's left as temp cause child node is the new inorder predecessor for the parent node and also it's the left child of the parent.
par -> lthread = true;
par -> left = temp;
Case 3
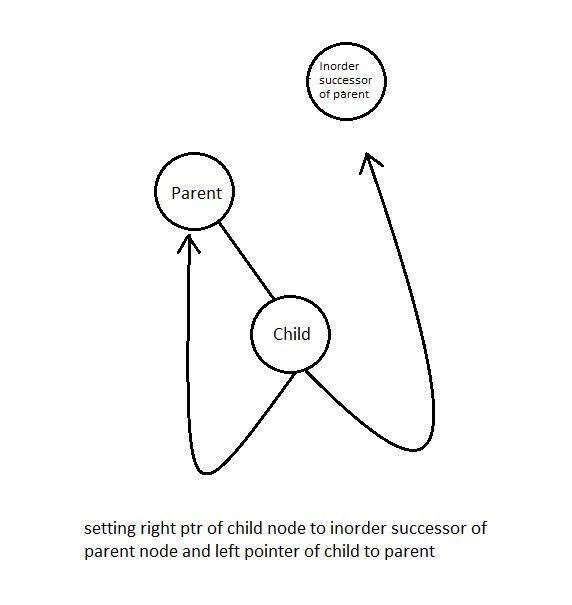
When new node is inserted as right child of some node we s perform two operations on the child and two operations on parent similar to what we have done in case 2 -
For Child
Let us say the new node inserted is child node and the node to which it's inserted is parent node then we can say that the parent of child inserted is now it's inorder predecessor and the inorder successor of parent is now the inorder succesor for the child node.
So the left and right threads of the new node will be -
// tmp represent child node here
tmp -> left = par;
tmp -> right = par -> right;
For Parent
The right pointer of parent node now points to it's newly inserted node and setting up it's bool variable to true indicating there exists a right child.
// par represents parent node here
par -> rthread = true;
par -> right = tmp;
Code for insertion
// Insert a Node in Binary Threaded Tree
struct Node *insert(struct Node *root, int ikey)
{
// Searching for a Node with given value
Node *ptr = root;
Node *par = NULL; // Parent of key to be inserted
while (ptr != NULL)
{
// If key already exists, return
if (ikey == (ptr->info))
{
printf("Duplicate Key !\n");
return root;
}
par = ptr; // Update parent pointer
// Moving on left subtree.
if (ikey < ptr->info)
{
if (ptr -> lthread == false)
ptr = ptr -> left;
else
break;
}
// Moving on right subtree.
else
{
if (ptr->rthread == false)
ptr = ptr -> right;
else
break;
}
}
// Create a new node
Node *tmp = new Node;
tmp -> info = ikey;
tmp -> lthread = true;
tmp -> rthread = true;
if (par == NULL)
{
root = tmp;
tmp -> left = NULL;
tmp -> right = NULL;
}
else if (ikey < (par -> info))
{
tmp -> left = par -> left;
tmp -> right = par;
par -> lthread = false;
par -> left = tmp;
}
else
{
tmp -> left = par;
tmp -> right = par -> right;
par -> rthread = false;
par -> right = tmp;
}
return root;
}
Time and space complexity for insertion
Time complexity - O(logn)
space complexiy - O(1)
Search operation in Threaded Binary Tree
Search operation in theaded binary tree is pretty simple we just need to follow a simple algorithm that is shown below
If search key < root then
Go to left thread
else
Go to right thread
we need to keep repeating the above algorithm until we find the required node , if we are unable to locate the node and reach null we can return -1 indicating that element doesn't exist in the tree.
Code
struct Node *search( struct Node *root , int key ){
Node *ptr = root ;
while( ptr != nullptr ){
if( ptr->info == key ){
// indicating that the element is found then
return ptr ;
}else if( ptr->info < key ){
// moving to inorder predecessor of the current node
ptr = ptr->right ;
}else{
// moving to inorder successor of the current node
ptr = ptr->left ;
}
}
// if element is not found then we can return nullptr indicating element not
// found in the given binary search tree
return nullptr ;
}
Time complexity for searching
Time complexity - O(logn)
Delete operation in Threaded Binary Tree
If we want to delete some node from the given doubly threaded binary search tree then we can use the delete operation but in the delete operation there can be three cases for a node in a doubly threaded binary tree.
Case 1 leaf node needs to be deleted
if we are deleting any node which is on the leaf then it's parent's left or right thread need to be adjusted so if leaf is left child of the parent node then after deletion left thread of the parent node is made to point to left thread of the child
and parent's leftThread is set to false indicating parent is pointing to some inorder predecessor.
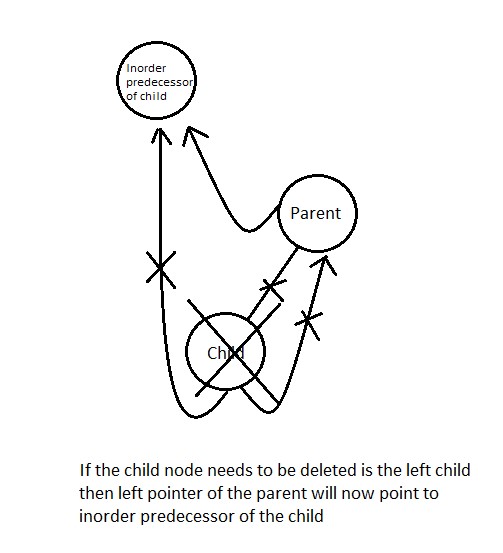
parent -> lthread = true;
parent -> left = ptr -> left;
similarly if we are deleting the right child then parent's right is made to point to right thread of child nd rightThread is set to false.
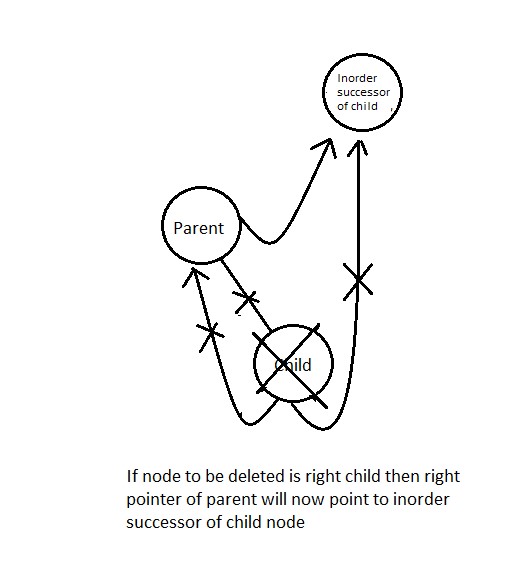
par -> rthread = true;
par -> right = ptr -> right;
Code for case 1
struct Node* case1(struct Node* root, struct Node* par,
struct Node* ptr)
{
// If Node to be deleted is root
if (par == NULL)
root = NULL;
// If Node to be deleted is left
// of its parent
else if (ptr == par->left) {
par->lthread = true;
par->left = ptr->left;
}
else {
par->rthread = true;
par->right = ptr->right;
}
// Free memory and return new root
free(ptr);
return root;
}
Case 2 node to be deleted has only 1 child left or right
Before deleting such node first it's inorder predecessor and inorder successor is found out -
s = inSucc(ptr);
p = inPred(ptr);
then
If Node to be deleted has left subtree, then after deletion right thread of its inorder predecessor should point to its inorder successor.
p->left = s;
If Node to be deleted has right subtree, then after deletion left thread of its inorder successor should point to its inorder predecessor .
s->left = p ;
Code for case 2
struct Node* case2(struct Node* root, struct Node* par,
struct Node* ptr)
{
struct Node* child;
// Initialize child Node to be deleted has
// left child.
if (ptr->lthread == false)
child = ptr->left;
// Node to be deleted has right child.
else
child = ptr->right;
// Node to be deleted is root Node.
if (par == NULL)
root = child;
// Node is left child of its parent.
else if (ptr == par->left)
par->left = child;
else
par->right = child;
// Find successor and predecessor
Node* s = inSucc(ptr);
Node* p = inPred(ptr);
// If ptr has left subtree.
if (ptr->lthread == false)
p->right = s;
// If ptr has right subtree.
else {
if (ptr->rthread == false)
s->left = p;
}
free(ptr);
return root;
}
Case 3 node to be deleted has 2 children
We find inorder successor of Node to be deleted and then we copy the information of this inorder successor into current Node. After this inorder successor Node is deleted using either Case 1 or Case 2 explained above.
// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case3(struct Node* root, struct Node* par,
struct Node* ptr)
{
// Find inorder successor and its parent.
struct Node* parsucc = ptr;
struct Node* succ = ptr->right;
// Find leftmost child of successor
while (succ->left != NULL) {
parsucc = succ;
succ = succ->left;
}
ptr->info = succ->info;
if (succ->lthread == true && succ->rthread == true)
root = case1(root, parsucc, succ);
else
root = case2(root, parsucc, succ);
return root;
}
Time and space complexity for deletion
Time complexity - O(logn)
space complexiy - O(1)
Code For Doubly Threaded Tree including insert,search and delete operations
#include <bits/stdc++.h>
using namespace std;
struct Node {
struct Node *left, *right;
int info;
// True if left pointer points to predecessor
// in Inorder Traversal
bool lthread;
// True if right pointer points to predecessor
// in Inorder Traversal
bool rthread;
};
struct Node *search( struct Node *root , int key ){
Node *ptr = root ;
while( ptr != nullptr ){
if( ptr->info == key ){
// indicating that the element is found then
return ptr ;
}else if( ptr->info < key ){
// moving to inorder predecessor of the current node
ptr = ptr->right ;
}else{
// moving to inorder successor of the current node
ptr = ptr->left ;
}
}
// if element is not found then we can return nullptr indicating element not
// found in the given binary search tree
return nullptr ;
}
// Insert a Node in Binary Threaded Tree
struct Node* insert(struct Node* root, int ikey)
{
// Searching for a Node with given value
Node* ptr = root;
Node* par = NULL; // Parent of key to be inserted
while (ptr != NULL) {
// If key already exists, return
if (ikey == (ptr->info)) {
printf("Duplicate Key !\n");
return root;
}
par = ptr; // Update parent pointer
// Moving on left subtree.
if (ikey < ptr->info) {
if (ptr->lthread == false)
ptr = ptr->left;
else
break;
}
// Moving on right subtree.
else {
if (ptr->rthread == false)
ptr = ptr->right;
else
break;
}
}
// Create a new Node
Node* tmp = new Node;
tmp->info = ikey;
tmp->lthread = true;
tmp->rthread = true;
if (par == NULL) {
root = tmp;
tmp->left = NULL;
tmp->right = NULL;
}
else if (ikey < (par->info)) {
tmp->left = par->left;
tmp->right = par;
par->lthread = false;
par->left = tmp;
}
else {
tmp->left = par;
tmp->right = par->right;
par->rthread = false;
par->right = tmp;
}
return root;
}
// Returns inorder successor using left
// and right children (Used in deletion)
struct Node* inSucc(struct Node* ptr)
{
if (ptr->rthread == true)
return ptr->right;
ptr = ptr->right;
while (ptr->lthread == false)
ptr = ptr->left;
return ptr;
}
// Returns inorder successor using rthread
// (Used in inorder)
struct Node* inorderSuccessor(struct Node* ptr)
{
// If rthread is set, we can quickly find
if (ptr->rthread == true)
return ptr->right;
// Else return leftmost child of right subtree
ptr = ptr->right;
while (ptr->lthread == false)
ptr = ptr->left;
return ptr;
}
// Printing the threaded tree
void inorder(struct Node* root)
{
if (root == NULL)
printf("Tree is empty");
// Reach leftmost Node
struct Node* ptr = root;
while (ptr->lthread == false)
ptr = ptr->left;
// One by one print successors
while (ptr != NULL) {
printf("%d ", ptr->info);
ptr = inorderSuccessor(ptr);
}
}
struct Node* inPred(struct Node* ptr)
{
if (ptr->lthread == true)
return ptr->left;
ptr = ptr->left;
while (ptr->rthread == false)
ptr = ptr->right;
return ptr;
}
// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case1(struct Node* root, struct Node* par,
struct Node* ptr)
{
// If Node to be deleted is root
if (par == NULL)
root = NULL;
// If Node to be deleted is left
// of its parent
else if (ptr == par->left) {
par->lthread = true;
par->left = ptr->left;
}
else {
par->rthread = true;
par->right = ptr->right;
}
// Free memory and return new root
free(ptr);
return root;
}
// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case2(struct Node* root, struct Node* par,
struct Node* ptr)
{
struct Node* child;
// Initialize child Node to be deleted has
// left child.
if (ptr->lthread == false)
child = ptr->left;
// Node to be deleted has right child.
else
child = ptr->right;
// Node to be deleted is root Node.
if (par == NULL)
root = child;
// Node is left child of its parent.
else if (ptr == par->left)
par->left = child;
else
par->right = child;
// Find successor and predecessor
Node* s = inSucc(ptr);
Node* p = inPred(ptr);
// If ptr has left subtree.
if (ptr->lthread == false)
p->right = s;
// If ptr has right subtree.
else {
if (ptr->rthread == false)
s->left = p;
}
free(ptr);
return root;
}
// Here 'par' is pointer to parent Node and 'ptr' is
// pointer to current Node.
struct Node* case3(struct Node* root, struct Node* par,
struct Node* ptr)
{
// Find inorder successor and its parent.
struct Node* parsucc = ptr;
struct Node* succ = ptr->right;
// Find leftmost child of successor
while (succ->lthread==false) {
parsucc = succ;
succ = succ->left;
}
ptr->info = succ->info;
if (succ->lthread == true && succ->rthread == true)
root = case1(root, parsucc, succ);
else
root = case2(root, parsucc, succ);
return root;
}
// Deletes a key from threaded BST with given root and
// returns new root of BST.
struct Node* deleteFromThreadedBst(struct Node* root, int target)
{
// Initialize parent as NULL and
// Node as root.
struct Node *par = NULL, *ptr = root;
// Set true if key is found
int found = 0;
// Search key in BST : find Node and its
// parent.
while (ptr != NULL) {
if (target == ptr->info) {
found = 1;
break;
}
par = ptr;
if (target < ptr->info) {
if (ptr->lthread == false)
ptr = ptr->left;
else
break;
}
else {
if (ptr->rthread == false)
ptr = ptr->right;
else
break;
}
}
if (found == 0)
printf("target not present in tree\n");
// Two Children
else if (ptr->lthread == false && ptr->rthread == false)
root = case3(root, par, ptr);
// Only Left Child
else if (ptr->lthread == false)
root = case2(root, par, ptr);
// Only Right Child
else if (ptr->rthread == false)
root = case2(root, par, ptr);
// No child
else
root = case1(root, par, ptr);
return root;
}
// Driver Program
int main()
{
struct Node* root = NULL , *temp = NULL;
root = insert(root, 1);
root = insert(root, 3);
root = insert(root, 5);
root = insert(root, 7);
root = insert(root, 12);
root = insert(root, 2);
root = insert(root, 10);
root = insert(root, 6);
temp = search(root , 5) ;
if( temp ) cout<<"Element with value 5 found\n" ;
else cout<<"element doesn't exist in the given binary threaded tree\n" ;
root = deleteFromThreadedBst(root, 6);
inorder(root);
return 0;
}
Output:
Element with value 5 found
1 2 3 5 7 10 12
