
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we present 4 different approaches for Zig Zag Traversal of Binary Tree. The zigzag traversal of the binary tree can be better understood using below example:
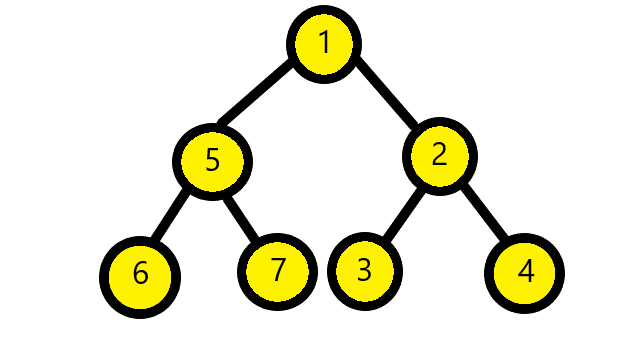
For the above tree, the zigzag traversal will be : 1 2 5 6 7 3 4
There are many approaches for this problem like:
- We can use two stacks and swap the values of these stacks at each level.
- We can use deque to solve problem. Depending upon the even or odd level we will push or pop.
- We can also use recursion. It will print the spiral binary tree.
- Last approach will use iteration. We will use two stacks for printing left to right stack.
Definition of node:
struct node{
int val;
struct node *left,*right;
}
Approach 1:
The problem can be solved using two stacks.They could be current and next. There would be another variable required to keep track of current level order. We will print values of the nodes after popping from the left to right. Then we push the nodes left child, then its right child to the stack next. The stack is a LIFO structure, when we pop the nodes from the next, it will be reversed.
When current order is right to left then the nodes get pushed with right child first and then their left child. At the end of each level we swap these stacks.
Algorithm:
- Firstly, we check if the root is null then we return else we move for next condition.
- We declare stack current and next.
- We push the root to current.
- Then we check if the stack is empty.
- If current is not empty then we pop the top of current from stack. We store it in temp.
- If temp is not null then, we print the data in it.
- To store the data according to current order, we check if current node is left node or right node. According to them we push the data.
- If current is empty then we swap current and next values.
Time Complexity: O(n)
Space Complexity: O(n) + O(n) = O(n)
void zigzag(struct node* root)
{
if (!root)
return;
stack<struct node*> current;
stack<struct node*> next;
current.push(root);
bool lefttoright = true;
while (!current.empty()) {
struct node* temp = current.top();
current.pop();
if (temp) {
cout << temp->data << " ";
if (lefttoright) {
if (temp->left)
next.push(temp->left);
if (temp->right)
next.push(temp->right);
}
else {
if (temp->right)
next.push(temp->right);
if (temp->left)
next.push(temp->left);
}
}
if (current.empty()) {
lefttoright = !lefttoright;
swap(current, next);
}
}
}
Approach 2:
- This approach uses a deque to solve problem. Depending upon the even or odd level we will push or pop.
- We start the solution from level 1.
- We start a loop till the queue is empty, we will pop the values from it if the level is even.
- When level is odd then if the temp is left then we push value in q, and push value of node in v.
- If temp is right then we push the right node of temp in q and its value in v.
- We will keep incrementing the level till the loop stops.
- In the end we return v.
vector<int> zigzag(node* root)
{
deque<node*> q;
vector<int> v;
q.push_back(root);
v.push_back(root->data);
node* temp;
int l = 1; //level
while (!q.empty()) {
int n = q.size();
for (int i = 0; i < n; i++) {
if (l % 2 == 0) {
temp = q.back();
q.pop_back();
}
else {
temp = q.front();
q.pop_front();
}
if (l % 2 != 0) {
if (temp->right) {
q.push_back(temp->right);
v.push_back(temp->right->data);
}
if (temp->left) {
q.push_back(temp->left);
v.push_back(temp->left->data);
}
}
else if (l % 2 == 0) {
if (temp->left) {
q.push_front(temp->left);
v.push_back(temp->left->data);
}
if (temp->right) {
q.push_front(temp->right);
v.push_back(temp->right->data);
}
}
}
l++;
}
return v;
}
Approach 3:
In this approach we use recursion. It will print the spiral binary tree.
- We will print the nodes in different levels in lterating order.
- We use a bool variable to change printing order of levels.
- If itr is equivalent to 1 then we print nodes left to right.
- Else we print nodes right to left.
- We will complement value of bool variabe in each iteration to change order.
We will use two functions in this approach, function level, function height and function zig zag. We will use level function to print nodes at various levels in tree. Function height will be used to check height of the tree and function zigzag we will print the zigzag traversal result.
Function Level:
void Level(struct node* root, int level, int l)
{
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1)
{
if (l)
{
Level(root->left,level - 1, l);
Level(root->right,level - 1, l);
}
else
{
Level(root->right,level - 1, l);
Level(root->left,level - 1, l);
}
}
}
Function height:
- In this function we will check the height of a tree.
- We start by checking ig the node is null. If so then we return 0.
- Else we compute the height of each subtree. In recrusive fashion we iterate the call left and right subtree.
- Then we check if left height is greater or right subtree height. We return the greater height + 1.
int height(struct node* node)
{
if (node == NULL)
return 0;
else
{
int left = height(node->left);
int right = height(node->right);
if (left > right)
return (left + 1);
else
return (right + 1);
}
}
Function zigzag:
- In this function we will print the zigzag traversal result. We initialise the height of tree using height function defined above.
- Then we initialise boolean ltr with false.
- Then we have for loop from 1 till height of tree. Here we call the Level function defined above in each iteration.
- We also revert ltr to traverse next level in opposite order.
void zigzag(struct node* root)
{
int h = height(root);
int i;
bool ltr = false;
for(i = 1; i <= h; i++)
{
Level(root, i, ltr);
ltr = !ltr;
}
}
Time complexity is: O(n^2).
The skewed trees give worst cases.
Approach 4:
- This is the iterative appproach. We will use two stacks for printing left to right stack.
- We use two stacks one for left to right and other for right to left.
- In each iteration, we have nodes of one level in one of the stack.
- We will print nodes, and then push nodes of next level in other stack.
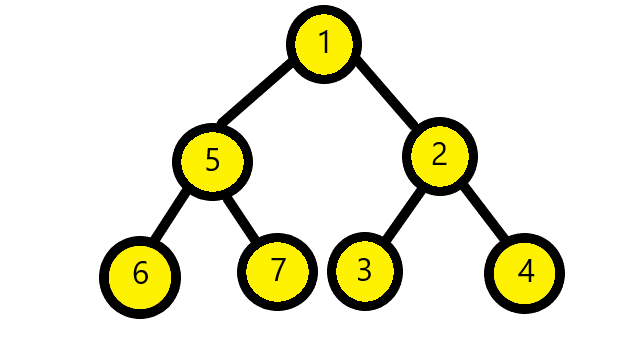
For the above tree, We check if the root is null or not. Since in the above tree it is not the case, we initialise s1 and s2 stack. Then we push the root to s1 stack.
Now we start iteration till s1 or s2 is not empty. Then we have another while loop within it. It will iterate till s1 is not empty. Then we have temp that will store the top node of s1. Which right now will be the root node. Then we pop the root node from the s1 stack and print the data of root node. If the right of the root node is not null then s2 will store the value temp. If the left of node is not null then we will store its value in s2.
This will store values for right to left.
Then we will enter another loop where we start by initialising value of top of s2 in temp. Then we pop top value of s2 and print its data. If the left of temp node is not null then we will store its value in s1. Then if the right of temp is not null then we will store its value in right of temp.
This will store values for left to right.
void spiral(struct node* root)
{
if (root == NULL)
return;
stack<struct node*> s1;
stack<struct node*> s2;
s1.push(root);
while (!s1.empty() || !s2.empty()) {
while (!s1.empty()) {
struct node* temp = s1.top();
s1.pop();
cout << temp->data << " ";
if (temp->right)
s2.push(temp->right);
if (temp->left)
s2.push(temp->left);
}
while (!s2.empty()) {
struct node* temp = s2.top();
s2.pop();
cout << temp->data << " ";
if (temp->left)
s1.push(temp->left);
if (temp->right)
s1.push(temp->right);
}
}
}
Therefore we can opt for any of the above approaches to find the zig zag manner of the tree. We can use stacks with complexity O(n), or we can use the dequeue approach, or the recursion approach or the iterative approach. Each of them will give us zig zag binary tree from the given binary tree.
