Convert Binary Tree to Threaded Binary Tree

In this article, we will focus on different approaches on how to convert a normal binary tree into a threaded binary tree. We will convert our binary tree to single threaded binary tree with right pointers pointing to inorder successor (if it exists).

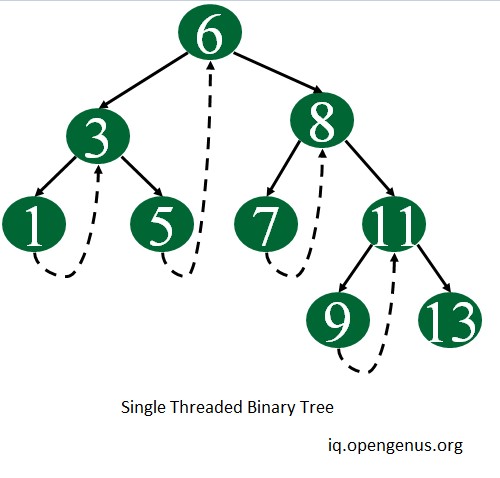
Approach 1

Naive Approach

We can do the inorder traversal of the tree and store it in some queue. Do another inorder traversal and where ever you find a node whose right reference is NULL , take the front element from the queue and make it the right of the current node.

This approach is easy to follow but the problem with this approach is it use extra memory and also it's traversing the tree two times which makes approach 1 quite heavy on space and time.

Time Complexity : O(n)
Space Complexity : O(n)

but instead of following this approach we can do better , so let's have a look at approach 2

Approach 2

Algorithm

1.Do the reverse inorder traversal, means visit right child first then parent followed by left.

2.In each recursive call also pass the node which you have visited before visiting current node .

3.In each recursive call whenever you encounter a node whose right pointer is set to NULL and previous visited node is set to not NULL then make the right pointer of node points to previously visited node and mark the boolean rightThread as true.

4. whenever making a new recursive call to right subtree, do not change the previous visited node and when making a recursive call to left subtree then pass the actual previous visited node.

5. Remember that when our right pointer of the current node is pointing to it's children then bool rightThread it set to true and if it is pointing to some of it's ancestor then rightThread is set to false.

This approach is better then the previous approach as this uses less time and much less constant space.

let' look at a example to see how we can use this algorithm to to convert a binary tree to threaded binary tree -

consider the following tree as example -

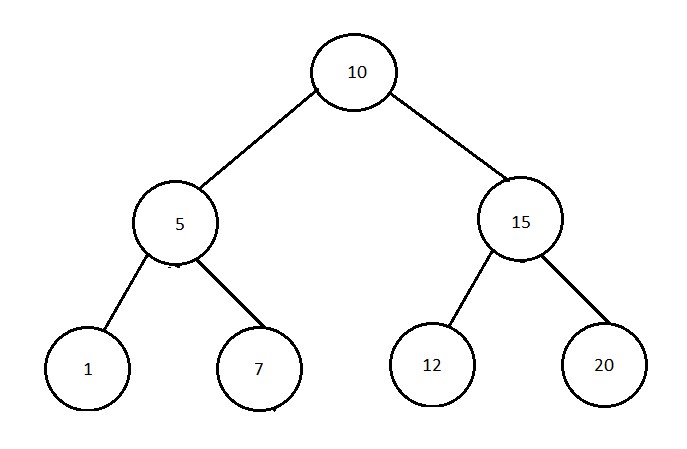
Step 1 :-
In the given tree we will traverse the tree in reverse inorder traversal which means we will first visit the right subtree then root then followed by the left subtree.

Step 2 :-
As we will follow this algorithm recrusively , so first we will visit the rightmost leaf node 20 , since there is no need which we have visited prior to this node we will make it's rightpointer point to NULL and bool variable as false.

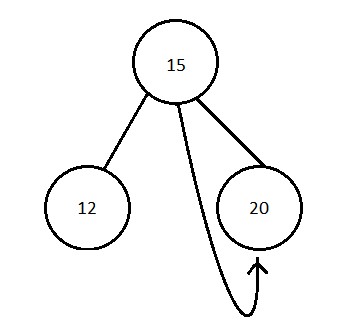
Step 3 :-
Now we will move to root which is node 15 in the given case and since we have already visited node 20 prior to node 15 so we will mark the right pointer of current node (15) to 20 and make bool but currently we are not on the leaf node so we will also make rightThread bool variable as true (indicating it's pointing to it's child node).

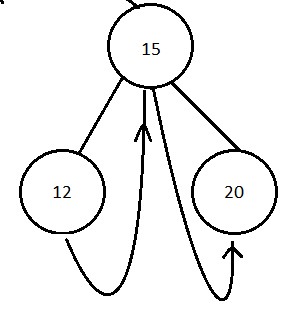
step 4 :-

we will again repeat the step three on node 12 but this is a leaf node whose right pointer is pointing to it's ancestor so we will set rightThread bool variable as false.

step 5 :-

We will just keep repeating the steps 2 , 3 and 4 until whole tree is traversed just keeping one thing mind - whenever we make a new recursive call to right subtree, do not change the previous visited node and when we make a recursive call to left subtree then pass the actual previous visited node .

step 6 :-

At the end we will have the whole binary tree converted to threaded binary tree.

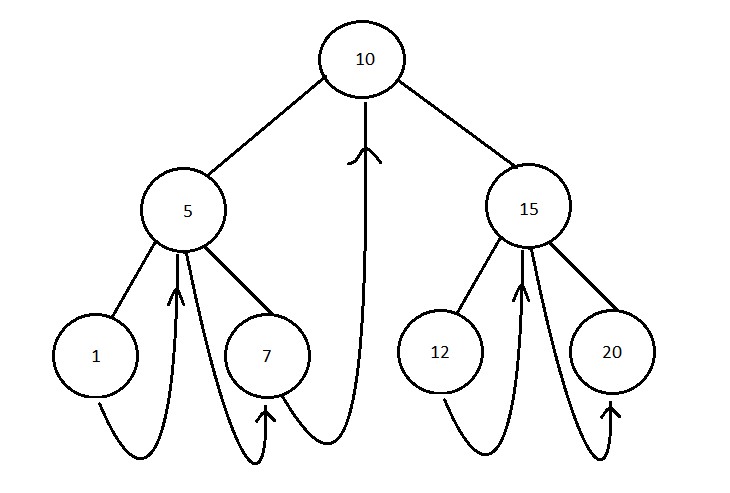
The time and space complexity required for the above conversion is -

Time Complexity : O(n)
Space Complexity : O(1)

Code

#include<iostream>
using namespace std ;

// struct and class having declared everything public is same in C++

class Node{
    public :
    Node *left;
    Node *right;
    int data;
    bool rightThread;
     Node(int data){
        this->data = data;
        rightThread = false;
        this->left = nullptr ;
        this->right = nullptr ;
    }
} ;

     Node* leftMostNode(Node *node){
        if(node==nullptr){
            return nullptr;
        }else{
            while(node->left!=nullptr){
                node = node->left;
            }
            return node;
        }
    }

class BSTtoThreadedBST {


    
    public :

    BSTtoThreadedBST(){

    }
     
    void convert(Node *root){
        inorder(root, nullptr);
    }

    void inorder(Node *root, Node *previous){

        if(root==nullptr){
            return;
        }else{
            inorder(root->right, previous);
            if(root->right==nullptr &&  previous!=nullptr){
                root->right = previous;
                root->rightThread=true;
            }
            inorder(root->left, root);
        }
    } ;

    void print(Node *root){
        //first go to most left node
        Node *current = leftMostNode(root);
        //now travel using right pointers
        while(current!=nullptr){
            cout<<" "<<current->data ;
            //check if node has a right thread
            if(current->rightThread)
                current = current->right;
            else // else go to left most node in the right subtree
                current = leftMostNode(current->right);
        }
        cout<<endl;
    }
} ;



   int main() {
        Node *root = new Node(10);
        root->left = new Node(5);
        root->right = new Node(15);
        root->left->left = new Node(1);
        root->left->right = new Node(7);
        root->right->left = new Node(12);
        root->right->right = new Node(20);
        

        BSTtoThreadedBST *converter = new BSTtoThreadedBST()  ;
        converter->convert(root);
       
        cout<<"Inorder Traversal: "<<endl;
        converter->print(root);

        return 0;
    }

Output

Inorder Traversal:
1 5 7 10 12 15 20

Thank you for reading!!