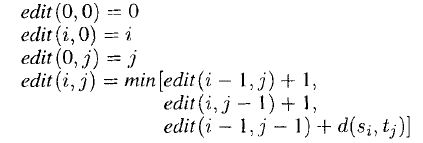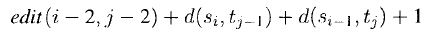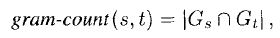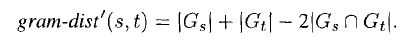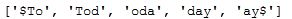Among the wide range of real world applications of Natural Language Processing (NLP) one of the most substantial and impactful is the spell correcting/checking techniques that have being developed and refined over the years of research and development, these techniques are being used in many of our day-to-day activities like word prediction while sending a text, spell checker while writing a word document, query prediction in search engines etc. Hence it is warranted that we go through how these algorithms have evolved over the years and how the effectiveness of these algorithms varies on using them individually or with conjunction with other algorithms.

In this article I will attempt to take a survey of these techniques and list out the major algorithms that have stood the test of time or have been used as an inspiration for more efficient algorithms for spell correction/checking.

We have explored the following:

• Early studies
• Approximate String Matching Techniques
  • String Similarity Measures
  • Phonetic Methods
• Coarse Search Techniques
  • N-gram indexing
  • Permuted Lexicon indexing
  • Phonetic Coding
• Fine Search Techniques
• Symmetric Speech Spell Correction Algorithm (SymSpell)
• Encoder-Decoder Sequence-to-Sequence Model

Early Studies

One of the earliest formal treatment of spell correction was due to Damerau (1964). The main method described in this paper assumes that any word which can not be found in the dictionary has at most one error which can be categorized into four categories:

• Word might me wrong
• Has one extra letter
• Missing one letter
• Has a single transposition i.e. a pair of adjacent letters in the word interchanged.

The author claims that nearly 80% of all the spelling errors made fall under the four above said classes.

A bit encoding used to create a dictionary by maintaining a 28-bit character register, first 26-bit is used for alphabets and remaining two bits are used for numerals and special character respectively, then a heuristic approach is used to compare strings of similar length with the query string and find if one if any any error is present or not

The method is less efficient by today's standards and more refined algorithms were needed.

We now further study the use of string matching techniques along with lexicon indexes to find approximate candidate matches of a query string in large lexicon.
We first lay out some widely used algorithms used to find the approximate matches of query string in a large lexicon, we call them approximate string matching techniques. Since a complete search of a large lexicon for every query string in computationally infeasible, some form of indexing is required to extract the likely candidates from the lexicon, i.e we do a coarse search of the given vocabulary. Once we have extracted the likely candidates, we perform fine search to refine our final results.

Approximate String Matching Techniques

1. String Similarity Measures

• Edit Distance - Due to Levenshtein (1965), it is one of the simplest form of string similarity measure, given two strings s and t of lengths m and n respectively, the edit distance between these string is the number of single character insertion and deletion needed to transform one string into another, the most commonly used operations that are allowed are
  1. insert a character into a string
  2. delete a character from a string
  3. replace a character of a string by another character
  

We employ a dynamic programming algorithm for this method which works in O(mn) time complexity. A matrix of (m+1)(n+1) is maintained and the (i,j) of the matrix will hold the the edit distance between the strings consisting of the first i characters of s and the first j characters of t. An outline of the algorithm given below
e.g. Edit distance between hordes and lords is two and edit distance between water and wine is 3

There are more sophisticated versions of edit-distance which consider moves, allocation of different costs to each kind of operation, for e.g. if the expression:

is added as an argument in the call to min, the resulting modified edit-distance algorithm allows transposition of letters with a cost of 1.
For e.g. for string 'thought' and 'thought' the modified edit distance will add 1 for transposition of letters th and ht in two string. This method is more powerful than the original algorithm but is expensive to compute.

• Agrep - A related class of string matching technique which reports two strings as matching if they are identical for at most K error, where K is specified by the user. The matching is binary and there is no notion of ranking i.e. the algorithm only returns if the query string matches any string in the lexicon or not.

• n-gram similarity measures - Technique was first introduced by Peterson (1980), n-gram of a string s in any substring of s of length n. A simple measure would be to choose n and count the number of common n-grams between two strings s and t.
  
  where G_x is the set of n-grams of string x.
  The above said measure does not take into consideration the length differences, e.g. board will have as many n-grams common with itself as it does with boardroom but they are not similar, as solution Ukkonen proposed an n-gram distance that can be defined as -
  

2. Phonetic Methods

• Soundex Method - By far the oldest phonetic method. It's a bucketing algorithm i.e. it buckets similarly sounding words together.Soundex uses code based on sound of each letter, codes are shown below -
  Given the query string s, the algorithm is as follows -
  1. Replace all but first letter of s by its phonetic code.
  2. Eliminate any consecutive repetitive codes.
  3. Eliminate all the vowels (i.e. code 0).
  4. Return the first four characters of the resulting string.
  For e.g. ashish will reduce to a2.

• Phonix - similar to Soundex, but prior to mapping, the letter group is transformed. There are as many as 160 phonetic transformations that are used in this algorithms few of them are (gn, ghn, gne) are trasformed to n, tjV is transformed to chV (where V is any vowel), x is transformed to ecs, etc.

Phonetic methods are relatively crude and are used rarely used in applications or or are used in conjunction with other algorithm.

Coarse Search Techniques

Some form of indexing on the available lexicon is required when approximate matches to a query term are to be retrieved. Without indexing, a complete search of the lexicon is required which is computationally expensive and impractical. This motivates the study of various indexing techniques used for coarse search.

1. N-gram indexing

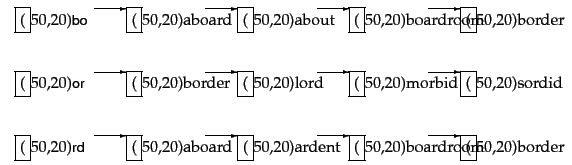
First we discuss how this scheme is used for pattern matching. An ordinal number is associated with each string in the lexicon and with each n-gram of the string is associated a postings list which is a list of ordinal number of words containing that n-gram. Given a pattern(i.e. a regular expression) the postings list of all the n-grams of the pattern are retrieved
For e.g a part of posting list of 2-gram index is shown below for the query term "bord" with bigrams "bo", "or" and "rd" -
For spell correction and string matching we may use the following method -
1. Take the union of all the string (s) in the postings list.
2. Find the gram-count(q,s) for all string s in the list and the query string q.
3. Use some efficient data structure like heap to store the gram-counts and identify the top matches for the query.
We can also use different methods like in the example given we can select the strings which contain at least two of the three given bigrams that would give us the output strings aboard, boardroom and border.

2. Permuted Lexicon indexing

For a fixed value of n, n-gram is a fixed length substring search. An alternative method is to use permuted lexicon indexing scheme which provides the access to the lexicon via substring of arbitrary length. In this scheme each string of the lexicon is rotated form of every word, e.g. representation of the word hello is shown below -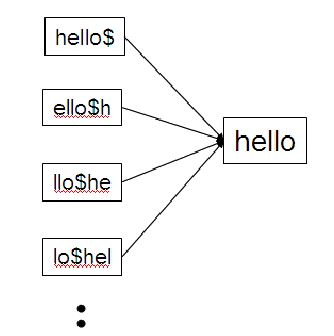
Where $ is string termination character. The lexicon is then sorted on the rotated form and the approximate matched of the query string q of length |q| is found as follows -

1. Binary search is used to find the locations of |q|+1 rotations of the string q.
2. Strings in the neighborhood of these locations are returned as matches.

This method is faster than the n-gram indexing scheme but is less efficient.

3. Phonetic Coding

This is a traditional coarse search scheme, it buckets the available vocabulary according to their phonetic sounds. For any query string q, the matching is binary and there is no notion of ranking and proximity, the phonetic coding is subjective and depends on the methods used such as Phonix or Soundex.
This method is ineffective so n-gram and permuted lexicon indexing scheme is preferred over it or used in conjunction with it.

Fine Search Techniques

After we query a string q in our indexed lexicon, we obtain a set of matching candidates as the results. There may be cases when these results constitute a significant chunk of the lexicon so there arises a need for further processing this result and filter out the irrelevant outputs.

For example if we use heaps as our data structure to extract the highest gram-count values after n-gram indexing we can enlarge this heap and hope if A answers are required they will occur in among kA highest gram-count values, for some user defined k.

Various other methods can be used like after n-gram indexing output we can further use Ukkonen's gram-dist(s,t) to refine the search space or after permuted lexicon indexing scheme we can use edit-distance algorithm, etc.

Now we look into some of the advanced methods of spell correction which are significantly faster than the traditional methods and are non-trivial

Symmetric Speech Spell Correction Algorithm (SymSpell)

Significant modification over the edit-distance algorithm, the proposed algorithm, SymSpell, is able to reduce the time complexity of candidate generation (coarse search) and dictionary lookup for a given string and for edit-distance n. It is approximately one million times faster than the traditional edit-distance algorithm discussed earlier in which we take into consideration the operations delete, transpose, replace and insert to calculate the edit-distance n.
In this algorithm only delete operation is required. Remaining operations transpose, insert and replace are transformed into delete operations to find the candidate matches in the given lexicon.
As an example, for an average 5 letter word and at a maximum edit distance of 3 we will have about about 3 million possible spelling errors, but SymSpell needs to generate only 25 deletes to cover them all.
We will look at a toy example of how we can implement SymSpell in python using symspellpy library.

#loading packages
import pkg_resources
from symspellpy.symspellpy import SymSpell, Verbosity

# build symspell tree 
sym_spell = SymSpell(max_dictionary_edit_distance=2, prefix_length=7)
#loading dictionary/lexicon
dictionary_path = pkg_resources.resource_filename(
    "symspellpy", "frequency_dictionary_en_82_765.txt")
# term_index is the column of the term and count_index is the
# column of the term frequency
sym_spell.load_dictionary(dictionary_path, term_index=0, count_index=1)

# lookup suggestions for single-word input strings
input_term = "memebers"  # misspelling of "members"
# max edit distance per lookup
print("Misspelled Word - ",input_term)
# (max_edit_distance_lookup <= max_dictionary_edit_distance)
suggestions = sym_spell.lookup(input_term, Verbosity.CLOSEST,
                               max_edit_distance=2)
# display suggestion term, term frequency, and edit distance
print("Best Candidate - ")
for suggestion in suggestions:
    print(suggestion)

Misspelled Word - memebers
Best Candidate -
members, 1, 22665615

Encoder-Decoder Sequence-to-Sequence Model

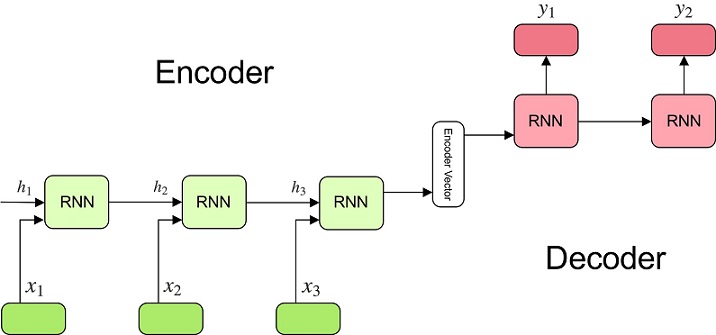
We now divert our attention to Sequence-to-Sequence (Seq2Seq) model which is a type of a neural network and basically consists of two parts - an encoder and a decoder.
The architecture of the model can be set up in many ways and one of the most prominent method is to use a Recurrent Neural Network (RNN), the first part is the encoding part which learns a lower dimensional representation of the input e.g. input may be the miss-spelled word and the second part is the decoding part which takes the output of the encoder as the input and gives back the output in accordance with the desired application e.g. decoder may output the correct spelling of the word fed to the encoder.
So as we can see, the encoder-decoder or the seq2seq model is one bigger neural network which comprises of two smaller neural networks namely an encoder and the decoder.
In the RNN architecture, each cell of the encoder takes two input, one input is the current input (e.g. the current character of the miss-spelled word) and the other one is the output from the previous cell and for the decoding part, each cell takes one input from the previous cell and generates a vector as the output (e.g. the candidate character for the current position in the correct word), this output may correspond to a character in our vocabulary.
An intuitive architecture of the model is given below -

Use of NLTK library of python to extract n-grams

Here we extract n-grams from a dummy sentence using Natural Language Toolkit of python

#importing required libraries
from nltk import ngrams
import numpy
#fuction to remove spaaces from a string
def remove(string): 
    return string.replace(" ", "") 

Next we construct a dummy sentence

vocab = "Today is a good day to learn natural language proccesing"
print("Sample Document - ",vocab)

Then we create a lexicon out of it

#contructing lexicon
lex = vocab.split(" ")
lex

Then we extract a single string from the lexicon and find the n-gram for specific n

spaced = ' '
for i in lex[0]:
    spaced = spaced + i + " "
spaced = "$ " + spaced + " $"

$ is used as beginning and end token of the string

n = 3
ngrams_ = ngrams(spaced.split(), n)
ngram_list  = []
for i in ngrams_:
    ngram_list.append((''.join([w + ' ' for w in i])).strip())
for i in range(len(ngram_list)):
    ngram_list[i] = remove(ngram_list[i])
ngram_list

Finally we get the output for single string as follows -

To find the n-gram for all the strings of the lexicon we use the following function

ngram_list  = []
for word in lex:
    spaced = ' '
    for i in word:
        spaced = spaced + i + " "
    spaced = "$ " + spaced + " $"
    n = 3
    ngrams_ = ngrams(spaced.split(), n)
    l = []
    for i in ngrams_:
        l.append((''.join([w + ' ' for w in i])).strip())
    for i in range(len(l)):
        l[i] = remove(l[i])
    ngram_list.append(l)
ngram_list

Conclusion

In their paper, Zobel and Dart have analysed each of the traditional methods discussed above and come to a conclusion that n-gram indexing provides an excellent coarse search mechanism for identifying approximate matches in a large lexicon. N-gram indexes used together with a fine search mechanism like the one proposed by Ukkonen can more than double the effectiveness.
They further conclude that although phonetic coding mechanism is fast and uses less space it is a poor string matching mechanism with effectiveness lower than that of other schemes.
However SymSpell and Seq2Seq models outperform all the traditional methods.

References and Further Readings

• List of Machine Learning (ML) topics
• A technique for computer detection and correction of spelling errors, Damerau (1964).
• Computer Programs for Detecting and Correcting Spelling Errors, Peterson (1980).
• Finding approximate matches in large lexicons, Zobel and Dart (1995).
• NIPS paper: Sequence to Sequence Learning with Neural Networks