
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In English language or any other language we generally notice that some words are used repeatedly and ranked highest in term of frequency like "the", "of", "to" etc. Ever wondered why? Frequency distribution is used to find out the statistical relationship between the text and the word count. Here we will be going to explore about this. But before moving on to Heap's Law lets get some heads on to the Zipf's Law.
Zipf's Law
The Zipf's Law is a statistical distribution in the dataset generally said as linguistic corpus, in which the frequency of the word is inversely proportional to their ranks. The distribution of word frequency count follows a simple mathematical relationship known as Zipf's Law. And the law examines the frequency of a linguistic corpa that how the most common word occurs twice as often as the second most common word and thrice as often as third subsequent word so on.
When words are positioned according to their frequencies in a large enough collection of texts and then the frequency is plotted against the rank, the outcome is a logarithmic curve. (Or if you graph on a log scale, the result is a straight line.)
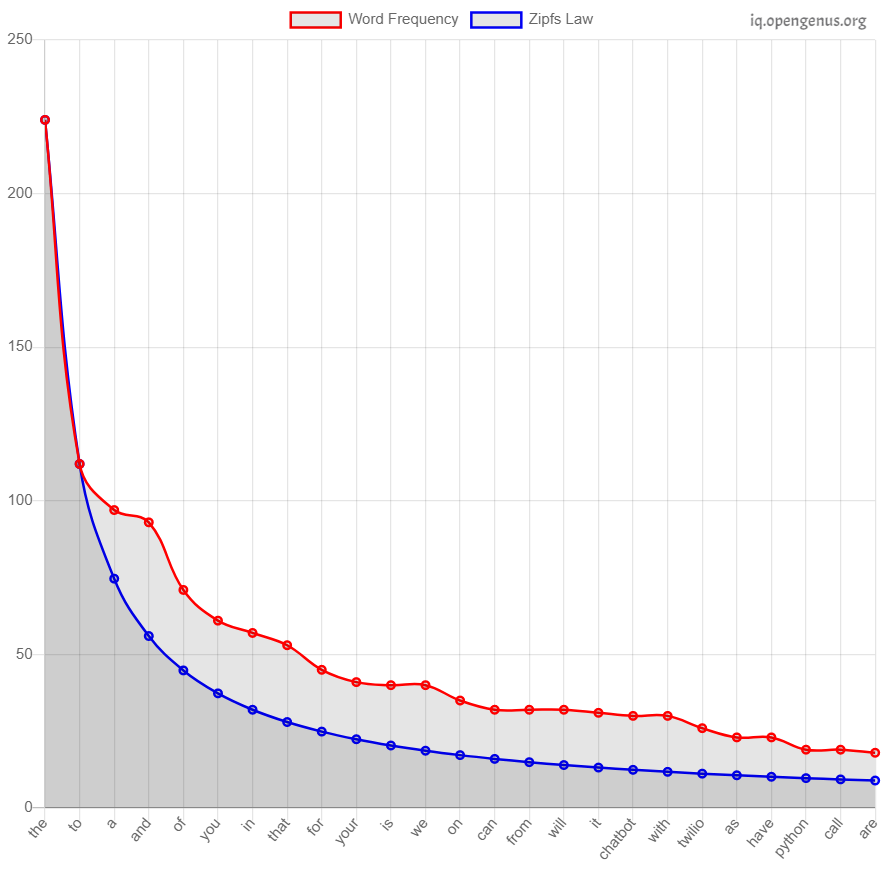
Fig.- Graph Plot of Word with their frequency
From the graph plot you can observe that from the sample text the have the highest frequency of 500 followed by second ranked word to with frequency of 215, which is in accordance with Zipf's law.
A Zipfian distribution of words is universal in natural language: It can be found in the speech of children less than 32 months old just as in the particular jargon of college course books. Studies show that this phenomenon likewise applies in essentially every language.
Did you know?
If you look at the Brown Corpus which contain a large amount of text, you will find an interesting thing that there are only 135 words which cover almost 50% of the amount of the total text. It even applies to the natural conversion that you all had , just 135 words account for 50% of everything we say.
The application of Zipf's Law can be seen in most of the Natural Language Processing algorithm and in the Text Compression.
- In the NLP, Zipf's law is used to generate the AI powered text that looks like a natural text and contains the words that a normal human use.
- For compressing a text we cannot simply remove the words of our choice, so the Compression algorithm make use of Zipf's law that compress the most frequent word in the text and doesn't alter the words that occurs least frequently.
We got the basic statistical approach of how Zipf's law is used. Another law is based on this is Heaps' Law
Heaps' Law
The law can be described like as the number of words in a document increases, the rate of the count of distinct words available in the document slows down.
The documented definition of Heaps’ law (also called Herdan's law) says that the number of unique words in a text of n words is approximated by
V(n) = K n^β
where K is a positive constant and β is between 0 and 1. K is often upto 100 and β is often between 0.4 an 0.6.
The relation of Zipf's law with the Heaps' law is observed like as the length of the document(words in the document) keeps on increasing then after certain point we can see that no much unique words are added to the vocabulary.
Let's have an example of how Heaps' Law work
Estimating vocabulary size with Heaps’ law
I will use the text document about the topic "Computer Science" from the Britannica website.
I experimented with different text size and the occurrence of unique words, and observed the relationship between the both.
The statistic distribution from the text is:
| n (Total number of word) | V (unique words) |
|---|---|
| 2100 | 728 |
| 4162 | 1120 |
| 6000 | 1458 |
| 8000 | 1800 |
| 10000 | 2022 |
Line Plot of the above statistical values is give below:-
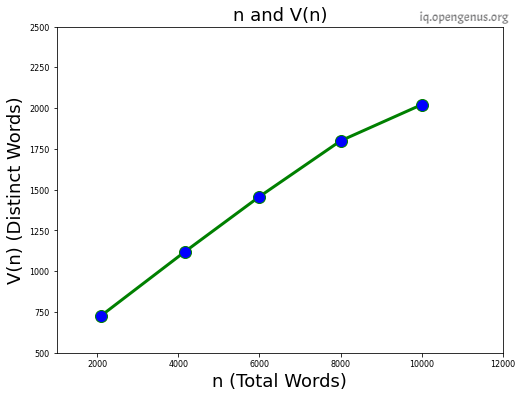
A very interesting finding can be observed from the above graph that at 2100 words, there are 728 unique words but that doesn't mean that doubling the total words i.e. 4162 will give double unique words but it will always the less than it therefore the unique words at n= 4162 is 1120.
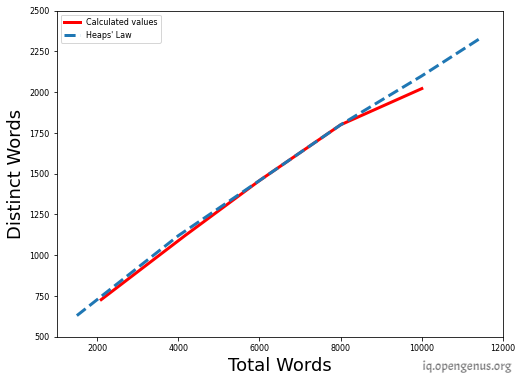
Now, we can be able to estimate the vocabulary size(unique words) of the same document if we are provided with the n(total number of the words). To predict that we first have to calculate the constant value K and β, for that we make use of the calculated value of V(n) and n and put that in V(n) = K n^β
V(n) = K n^β => log V(n) = β log(n) + K
Use, V(n) = 1458 and n = 6000
=> log(1458) = β log(6000) + K --(1)
V(n) = 1800 and n = 8000
=> log(1800) = β log(8000) + K --(2)
Solving (1) and (2) , we get β = 0.69 and K = 3.71
For example, for the 120000 total words Heaps' law predicts:
3.71 x 12000^0.69 = 2421 unique words.
The actual number of unique words in 12000 total words is 2340, which is very close to the predicted result.
The parameter k is quite variable and will reduce the growth rate of the vocabulary if stemming or lemmatisation is used whereas including numbers and spelling errors can increase it.
Heaps' law suggests that (i) the vocabulary size continues to expand with more documents in the collection, but the growth rate slows down and (ii) the size of the vocabulary is quite large for large collections.
The Heaps' Law is generally used in NLP, before training the model it can be used to get the size of the vocabulary using the Heaps' Law as we have size of the document and the size of the data available for training.
