Iterative post-order traversal

In this article, we have explained how to do Iterative post-order traversal of a Binary Tree using 3 different techniques along with complete implementation.

Basics:

• A binary search tree is a tree data structure where the key values of nodes in the left subtree are smaller than the key value of the root and the values of nodes in the right subtree are greater than the key value of the root.
• A tree traversal is visiting all the nodes in the tree exactly once. A post-order traversal is traversing the left subtree, the right subtree and then the root.
  Post-order traversal order - Left, Right, Root.

Stack based implementation and Morris post-order traversal are used to perform iterative post-order traversal.

1. Post-order traversal using 1 stack.
2. Post-order traversal using 2 stacks.
3. Morris post-order traversal.

Post-order traversal using 1 stack

• Here a single stack is used to remember the order of nodes to be explored. We need to traverse to the leftmost node of the binary tree, in this process, to preserve the order of nodes to be explored, root and root's right child are pushed to stack.
• If the leftmost node is reached and doesn't have a right child, pop it from the stack and print the key value of node.
• If the leftmost node has a right child, then push the right child, then the root to stack.

Algorithm

1. Create an empty stack and set node current as root.
2. Push the current's right child and next current itself to the stack and set current as current's left child.
3. Perform the following steps till the stack is empty.
4. Perform step 2 till the current value is null.
5. Pop from the stack and set the popped element as current.
6. If the popped element has a right child and the right child is at the top of the stack (obtained by performing peek() operation on stack), then pop the right child from stack and push current and then set current as current's right child.
7. Else, print the value of current node and set current to null.

Implementation in Java

Consider the following binary search tree:

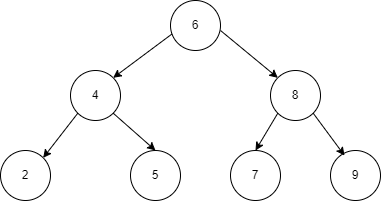
//Iterative postorder traversal using 1 stack

private void iterPostOrder1(Node root) {
    Stack < Node > stack = new Stack < Node > ();
    Node p = root;

    if (root == null)
        System.out.print("No nodes in Binary search tree");

    else {
        stack.push(p.right);
        stack.push(p);
        p = p.left;

        while (!stack.isEmpty()) {
            while (p != null) {
            
            //check if p has a right child
                if (p.right != null) {
                    stack.push(p.right);
                    stack.push(p);
                    p = p.left;
                } else {
                    stack.push(p);
                    p = p.left;
                }
            }
            
            p = stack.pop();
            if (!stack.isEmpty() && p.right != null && stack.peek() == p.right) {
                stack.pop();
                stack.push(p);
                p = p.right;
            } else {
                System.out.print(p.data + "  ");
                p = null;
            }
        }
    }
}

Output
2 5 4 7 9 8 6

Time complexity - O(N)
Space complexity - O(N)

Process visualization

A stack and the binary search tree are shown in the figures, violet color filled nodes represent the "current" node. The order of nodes printed below the stack in red is the order in which the node key values are printed.

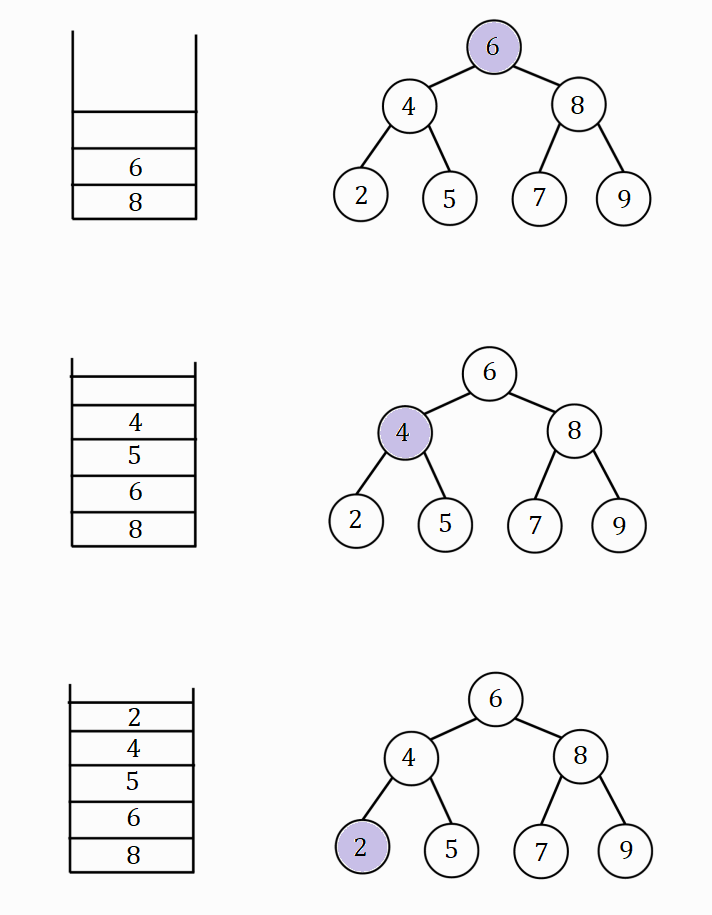
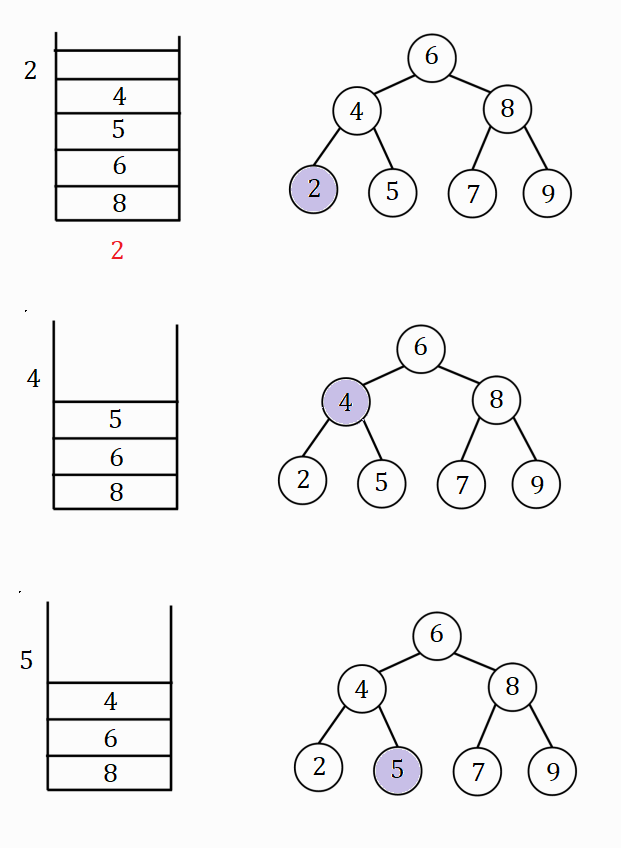
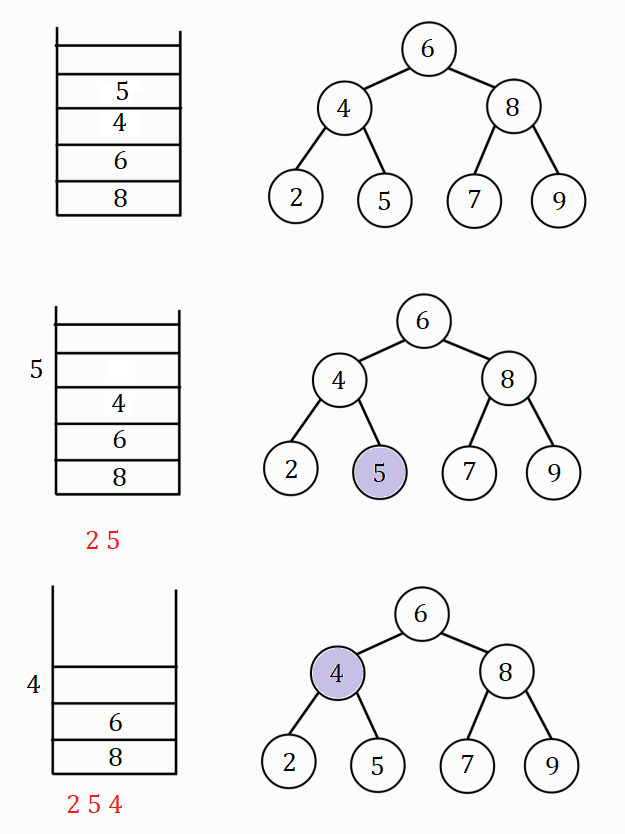
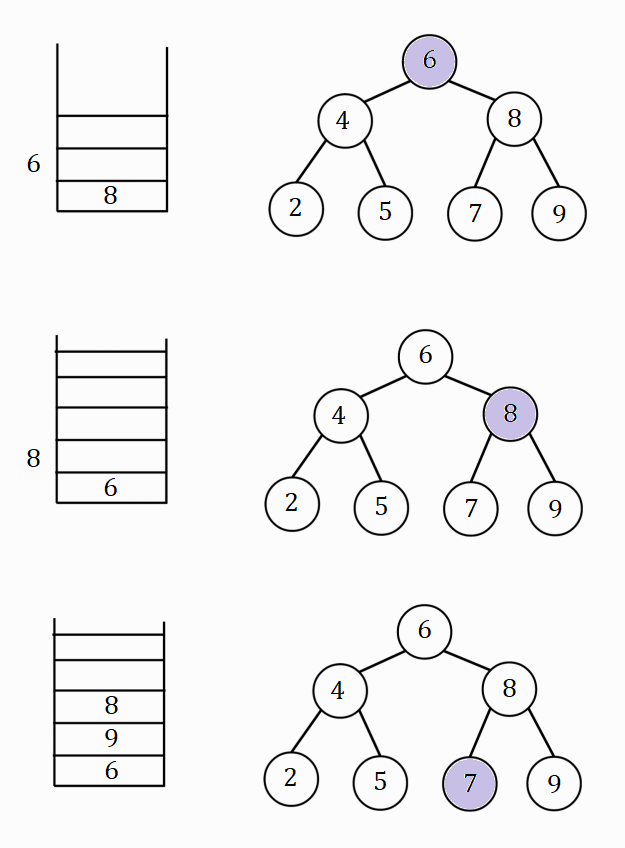
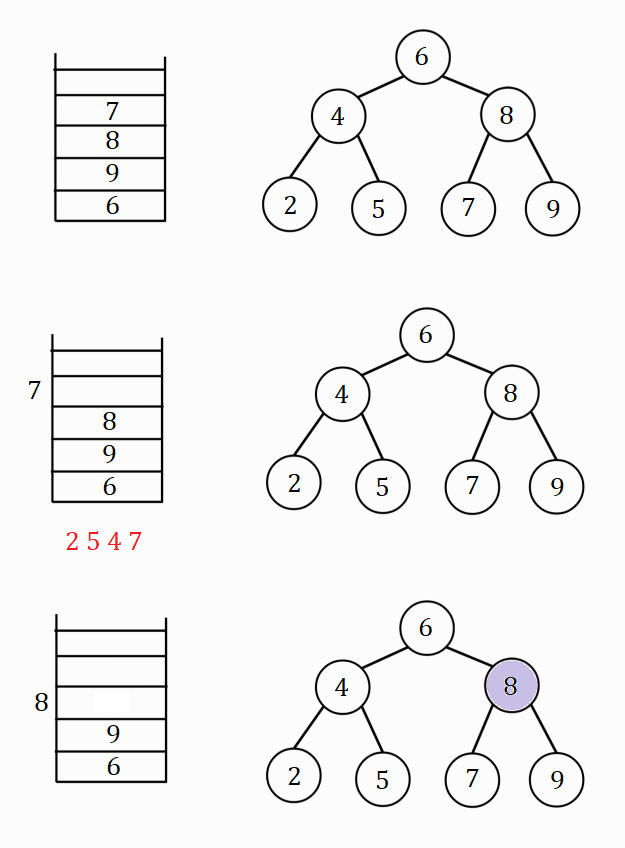
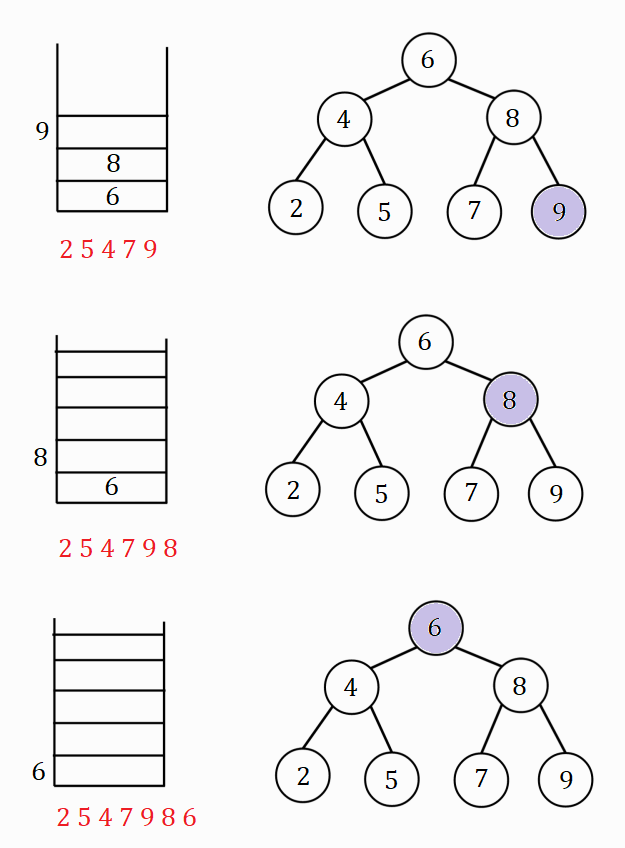
Hence the post-order traversal of the binary search tree is - 2 5 4 7 9 8 6

Post-order traversal using 2 stacks

In this method a second stack is used to obtain reverse post-order traversal, then the elements of the stack are popped to get the post-order traversal as a stack follows LIFO (Last In First Out) policy.

Algorithm

1. Create 2 stacks stack1 and stack2 and push the root node in stack1.
2. Do the steps 3 and 4 till stack1 is empty.
3. Pop an element from stack1 and push it in stack2 and then push the popped element's left and right children to stack1.
4. Pop the node elements from stack2 and print the key values one by one.

Implementation in Java

//iterative postorder traversal using 2 stacks

private void iterPostOrder2(Node root) {
    Stack < Node > stack0 = new Stack < Node > ();
    Stack < Node > stack1 = new Stack < Node > ();
    Node p = null;

    if (root == null)
        System.out.print("No nodes in Binary search tree");

    else {
        stack0.push(root);
        while (!stack0.isEmpty()) {
            p = stack0.pop();
            stack1.push(p);
            
            //check if p's left and right children exist
            if (p.left != null) stack0.push(p.left);
            if (p.right != null) stack0.push(p.right);
        }

        while (!stack1.isEmpty()) {
            p = stack1.pop();
            System.out.print(p.data + "  ");
        }
    }
}

Output
2 5 4 7 9 8 6

Time complexity - O(N)
Space complexity - O(N)

Process visualization

The stack diagrams are numbered in order at the bottom of each stack diagram.

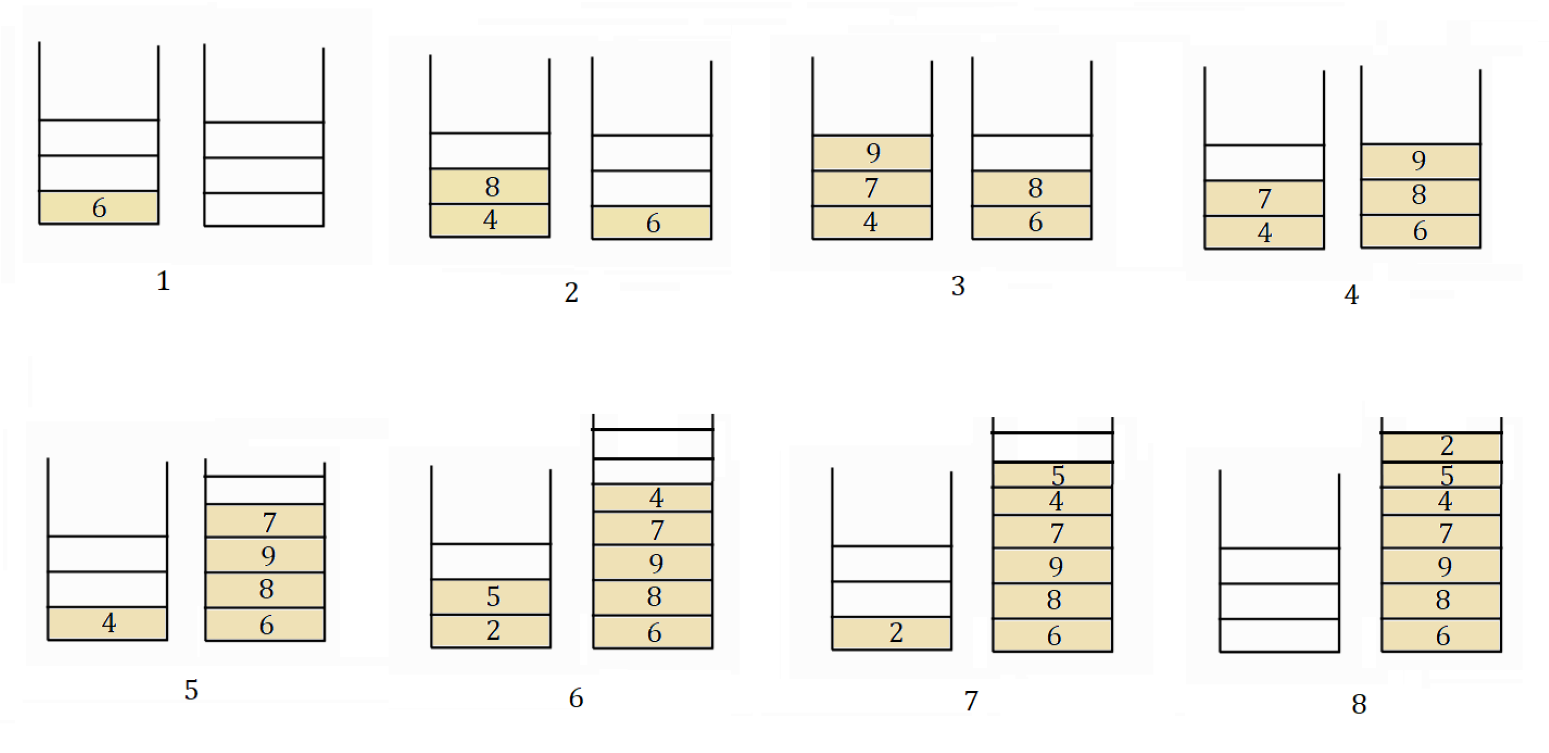
The elements of the second stack are popped one by one and the result is the post-order traversal of the tree.

Post-order traversal - 2 5 4 7 9 8 6

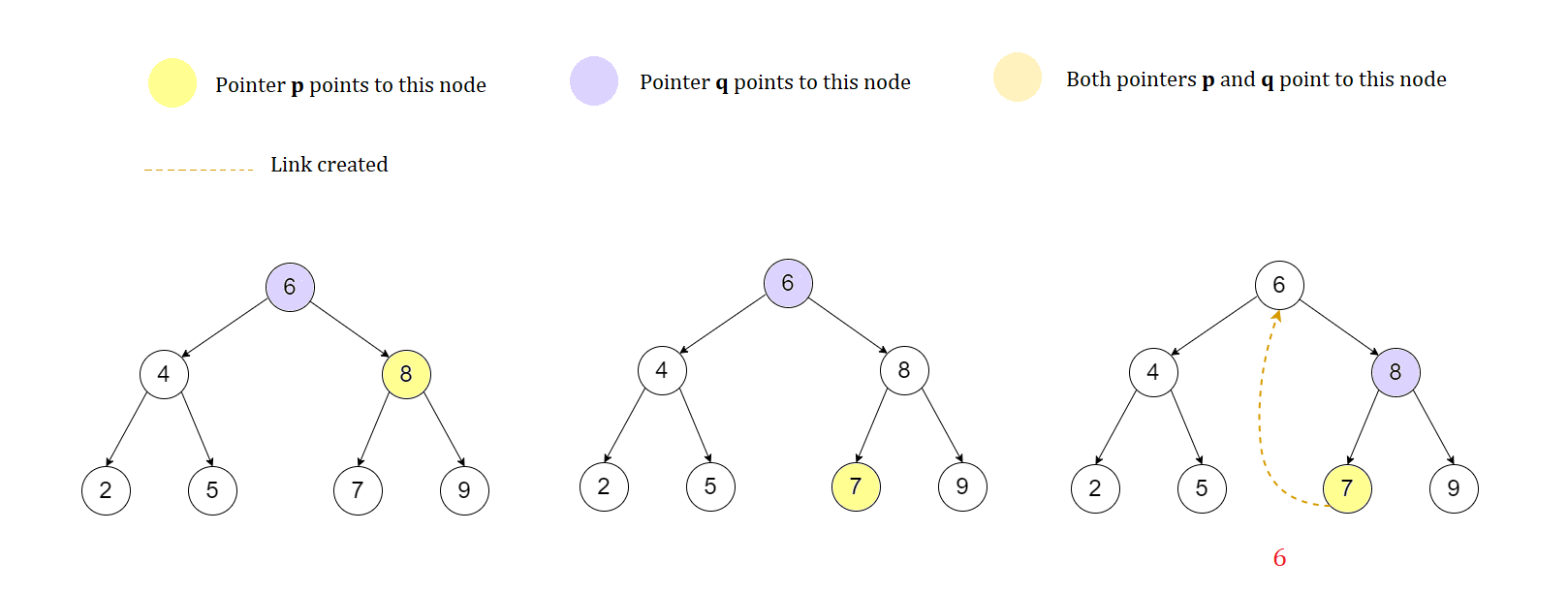
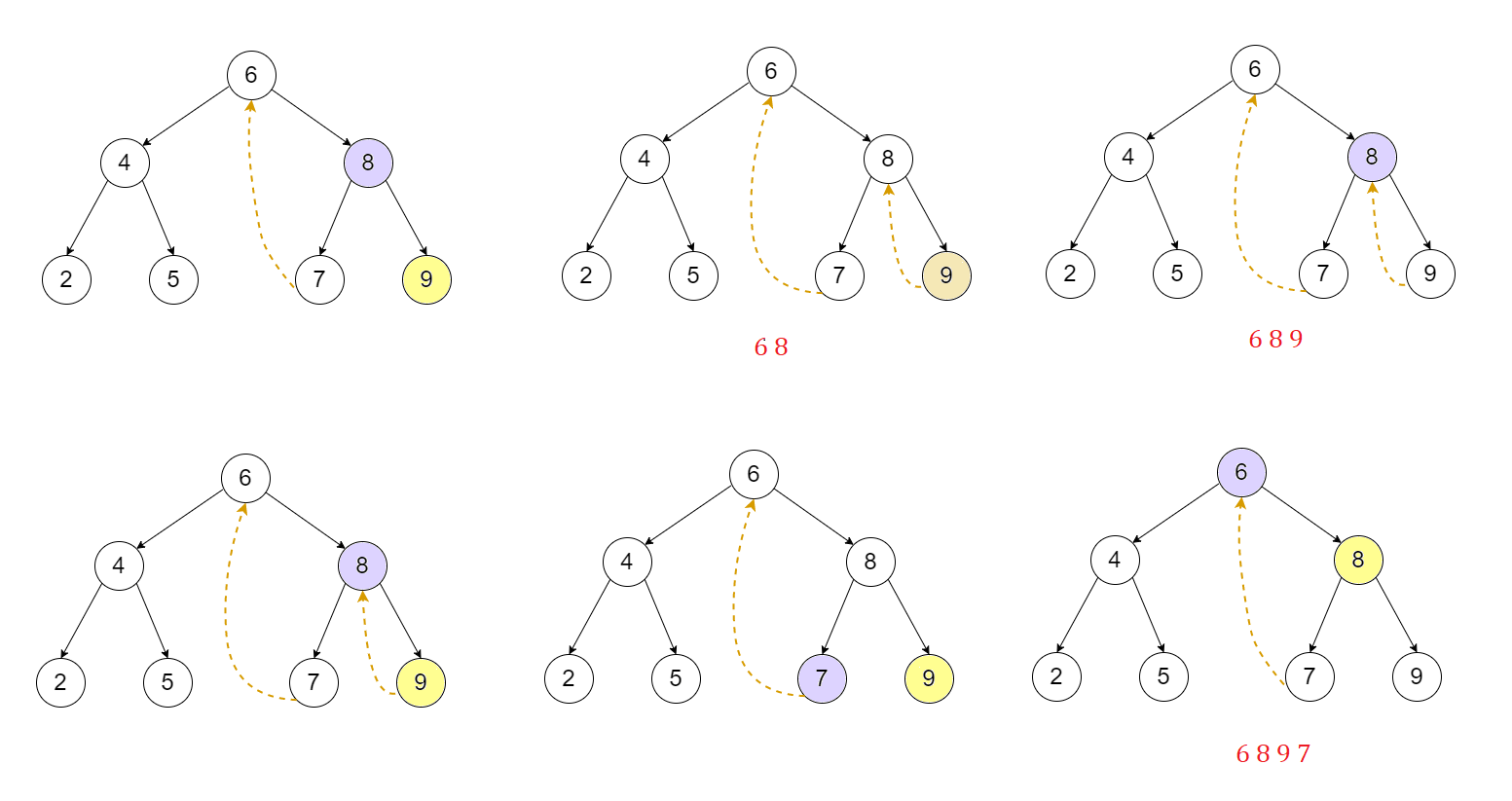
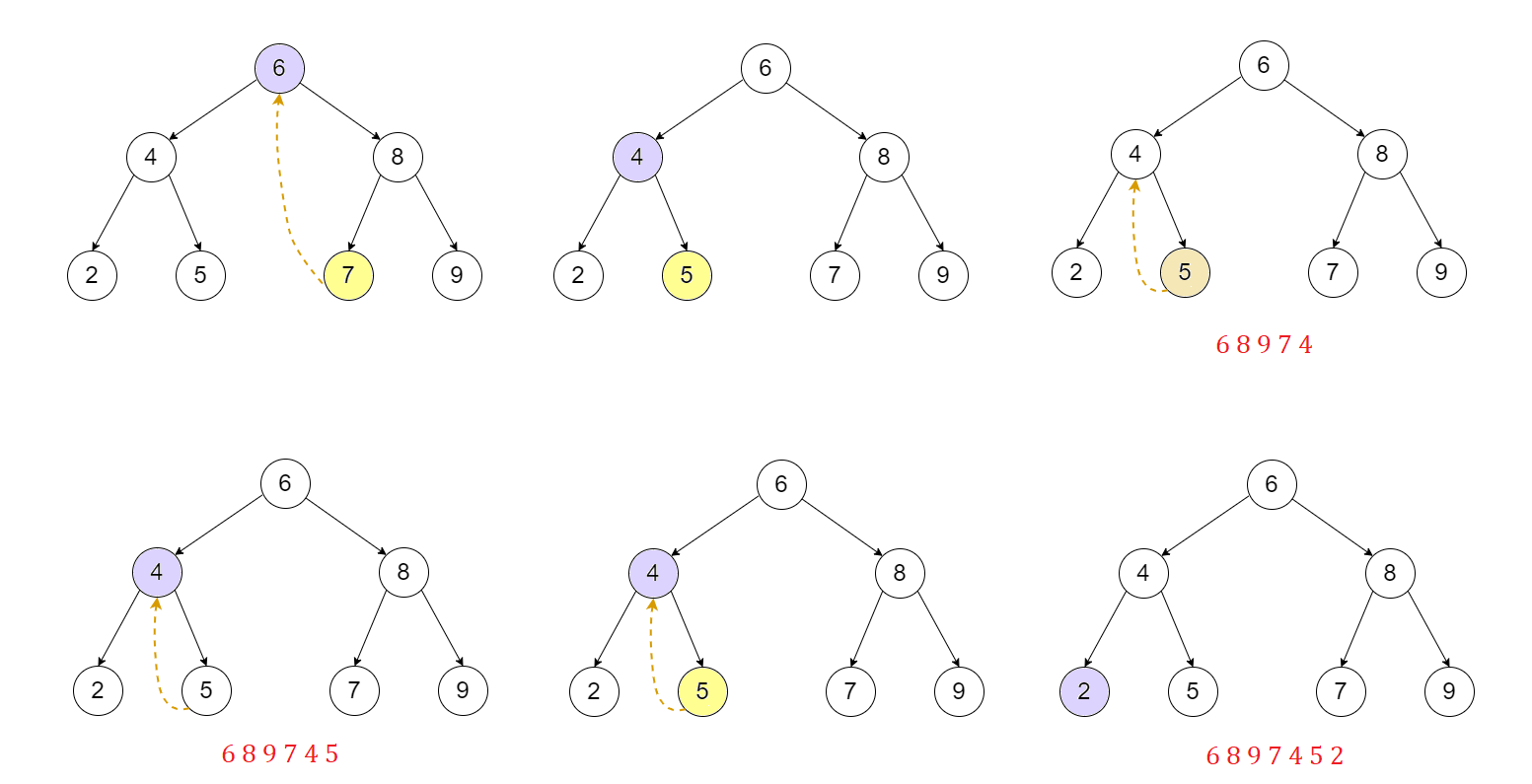
Morris Post-order Traversal

• Morris post-order traversal can be used to avoid recursion or using auxiliary stacks to find the post-order traversal of a binary tree. Here the binary tree is first threaded.
• Since leaf nodes don't have successor node, no other node can be reached from them, in a threaded binary tree, information is added to the nodes to allow for a linear traversal.
• A binary tree is threaded by making all the right child pointers which would be normally null point to the in-order successor of the node if it exists and all the left child pointers which would normally be null point to the in-order predecessor of the node.
• These pointers are modified when the node is traversed again to maintain the original structure of the tree.
• Predecessor is the rightmost node in left subtree if the left subtree is not NULL and if right subtree is not NULL, then successor is the leftmost node in right subtree.
• It saves memory and time as recursion is not used.

Algorithm

1. Set the current node to the root.
2. Do step-3 to step-7 till current node becomes null.
3. Check if current has a right subtree.
   • If step-3 is true then create a node "dummy" and set it to point to the right child of current.
   • If step-3 is false then add the current node key value to the list and update the current node to point to the left child of current.
4. Perform step-5 till dummy node's left child is equal to null or the dummy node's left child points to the same node as current node.
5. Update dummy node to point to its left child.
6. Check if dummy node's left child is null.
   • If step-6 is true then add current node key value to list and set dummy node's left child as current and update dummy node to make it point to it's right child.
   • If step-6 is false then set dummy node to point to null and update current node to it's left child.
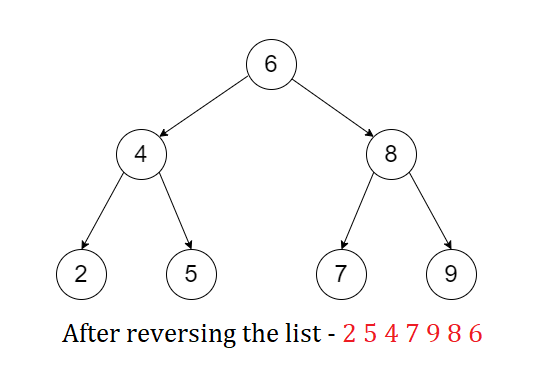
7. Reverse the list and print the post-order traversal of the tree.

Implementation in Java

public ArrayList < Integer > morrisTraversal(Node root) {
  ArrayList < Integer > arr = new ArrayList < Integer > ();

  Node p = root;

  while (p != null) {
  
  //check if p has a right subtree
    if (p.right == null) {
      arr.add(p.data);
      p = p.left;
    } else {
      Node q = p.right;
      while (q.left != p && q.left != null)
        q = q.left;

      if (q.left == null) {
        arr.add(p.data);
        q.left = p;
        p = p.right;
      } else {
        q.left = null;
        p = p.left;
      }
    }
  }

  Collections.reverse(arr);
  return arr;
}

Output
2 5 4 7 9 8 6

Time complexity - O(N)
Space complexity - O(1)

Process visualization

The diagrams are to be read left to right.

Binary search tree implementation

import java.util.*;

public class BinSearchTree {

//creating node class
  public class Node {
    private int data;
    private Node left;
    private Node right;

    Node() {
      this.data = null;
      this.left = null;
      this.right = null;
    }

    Node(int data) {
      this.data = data;
      this.left = null;
      this.right = null;
    }
  }
  
  private Node root;

  BinSearchTree() {
    root = null;
  }

  //insert a node in BST
  private Node insert(Node root, int data) {
    if (root == null) {
      root = new Node(data);
      return root;
    } else if (root.data > data) root.left = insert(root.left, data);

    else root.right = insert(root.right, data);

    return root;
  }

  //iterative postorder traversal using one stack
  private void iterPostOrder1(Node root) {
    Stack < Node > stack = new Stack < Node > ();
    Node p = root;

    if (root == null)
      System.out.print("No nodes in Binary search tree");

    else {
      stack.push(p.right);
      stack.push(p);
      p = p.left;

      while (!stack.isEmpty()) {
        while (p != null) {
        
        //check if right subtree exists
          if (p.right != null) {
            stack.push(p.right);
            stack.push(p);
            p = p.left;
          } else {
            stack.push(p);
            p = p.left;
          }
        }

        p = stack.pop();
        if (!stack.isEmpty() && p.right != null && stack.peek() == p.right) {
          stack.pop();
          stack.push(p);
          p = p.right;
        } else {
          System.out.print(p.data + "  ");
          p = null;
        }
      }
    }
  }


  //iterative postorder traversal using 2 stacks
  private void iterPostOrder2(Node root) {
  
  //creating 2 stacks using stack class
    Stack < Node > stack0 = new Stack < Node > ();
    Stack < Node > stack1 = new Stack < Node > ();
    Node p = null;

    if (root == null)
      System.out.print("No nodes in Binary search tree");

    else {
      stack0.push(root);
      while (!stack0.isEmpty()) {
        p = stack0.pop();
        stack1.push(p);

        //checking if p's left and right children exist.
        if (p.left != null) stack0.push(p.left);
        if (p.right != null) stack0.push(p.right);
      }

      while (!stack1.isEmpty()) {
        p = stack1.pop();
        System.out.print(p.data + "  ");
      }
    }
  }

  public void insertNode(int data) {
    this.root = insert(this.root, data);
  }

  public void postorder2() {
    iterPostOrder2(this.root);
  }

  public void postorder1() {
    iterPostOrder1(this.root);
  }

  public ArrayList < Integer > postorder3() {
    ArrayList < Integer > arr = new ArrayList < Integer > ();
    arr = morrisTraversal(root);
    return arr;
  }

  public ArrayList < Integer > morrisTraversal(Node root) {
    ArrayList < Integer > arr = new ArrayList < Integer > ();

    Node p = root;

    while (p != null) {
    
    //check if right subtree of p exists
      if (p.right == null) {
        arr.add(p.data);
        p = p.left;
      } else {
        Node q = p.right;
        while (q.left != p && q.left != null)
          q = q.left;

        if (q.left == null) {
          arr.add(p.data);
          q.left = p;
          p = p.right;
        } else {
          q.left = null;
          p = p.left;
        }
      }
    }

    Collections.reverse(arr);
    return arr;
  }
  public static void main(String[] args) {
    BinSearchTree tree = new BinSearchTree();
    tree.insertNode(6);
    tree.insertNode(4);
    tree.insertNode(8);
    tree.insertNode(2);
    tree.insertNode(5);
    tree.insertNode(7);
    tree.insertNode(9);
    tree.postorder1();
    List result = tree.postorder3();
    for (int i = 0; i < result.size(); i++)
      System.out.print(result.get(i) + " ");
  }
}

With this article at OpenGenus, you must have the complete idea of Iterative post-order traversal.