Layer Normalization: An Essential Technique for Deep Learning Beginners

Introduction

Deep learning has become one of the most powerful machine learning techniques in recent years. Neural networks are at the heart of deep learning and have shown great performance in various tasks, such as image recognition, speech recognition, and natural language processing. However, training neural networks can be challenging due to issues such as vanishing gradients and overfitting. To address these challenges, normalization techniques have been developed, one of which is layer normalization.

History and Evolution

Layer normalization is a relatively new technique in the field of deep learning. It was first introduced by Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey Hinton in their 2016 paper "Layer Normalization". The technique was developed as an alternative to batch normalization, which had become a popular method for normalizing activations in neural networks.

Batch normalization involves normalizing the activations in a batch of training examples by subtracting the mean and dividing by the standard deviation. While batch normalization can be effective, it has some drawbacks, including sensitivity to batch size and the order of training examples. Layer normalization was developed as a way to address these issues.

Layer normalization operates on a single training example at a time, rather than a batch of examples. It normalizes the activations of each layer by subtracting the mean and dividing by the standard deviation of the layer's activations. This approach has been shown to be effective in a wide range of tasks, including image recognition, natural language processing, and speech recognition.

Since its introduction, layer normalization has been the subject of numerous research studies and has been shown to be effective in a variety of neural network architectures. It has also been used in combination with other normalization techniques, such as weight normalization, to further improve the performance of neural networks.

Overall, layer normalization represents a significant evolution in the field of deep learning and has the potential to improve the performance and stability of neural networks in many applications till date.

What is Layer Normalization?

Layer normalization is a technique used in deep learning that aims to improve the performance and stability of neural networks. It is a type of normalization that is applied to the activations of neurons within a layer. The goal of layer normalization is to ensure that the distribution of activations is centered around zero and has a unit variance.

How Does Layer Normalization Work?

In a neural network, each neuron in a given layer takes the weighted sum of the outputs of the neurons in the previous layer, applies an activation function to that sum, and then outputs its own value to the next layer. The activation function introduces non-linearity into the neural network and allows it to learn complex patterns in the data.

The purpose of layer normalization is to make the distribution of the inputs to each neuron more consistent across training examples. To achieve this, layer normalization computes the mean and standard deviation of the activations of each neuron in a given layer, and then normalizes the activations using these statistics. This is similar to batch normalization, but instead of normalizing over the entire batch, we normalize over the activations within each layer.

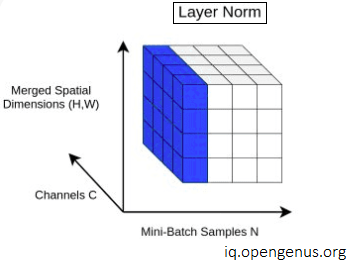
The formula for layer normalization is as follows:

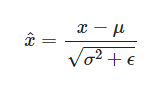
Explore the reason behind adding epsilon in the denominator.

Benefits of Layer Normalization

Layer normalization offers several benefits over other normalization techniques such as batch normalization. One of the main benefits is that it can improve the stability of the training process. By making the distribution of activations more consistent, layer normalization can prevent the vanishing gradient problem, which occurs when gradients become very small during backpropagation and cause the network to stop learning. Layer normalization can also reduce the impact of outliers in the training data, which can be useful in some applications.

Another benefit of layer normalization is that it can improve the generalization performance of the neural network. By reducing the impact of small changes in the input distribution, layer normalization can make the network more robust to changes in the data. This can be especially useful in applications where the input distribution can change over time, such as in natural language processing.

Applications of Layer Normalization

Layer normalization has been shown to be effective in a wide range of tasks, including image recognition, natural language processing, and speech recognition. It can be applied at different levels of the neural network, such as after each fully connected or convolutional layer. It has also been used in combination with other normalization techniques, such as weight normalization, to improve the performance of neural networks.

Conclusion

Layer normalization is a powerful technique that can improve the performance and stability of neural networks. By making the distribution of activations more consistent, layer normalization can prevent the vanishing gradient problem and reduce the impact of outliers in the training data. It can also improve the generalization performance of the neural network by reducing the impact of small changes in the input distribution.

Layer normalization is a relatively simple technique to implement, and has been shown to be effective in a wide range of tasks, including image recognition, natural language processing, and speech recognition. It can be applied at different levels of the neural network, such as after each fully connected or convolutional layer. It has also been used in combination with other normalization techniques, such as weight normalization, to further improve the performance of neural networks.

Test yourself by answering this simple question.