Max path sum between two nodes in Binary Tree

In this article, we have explored algorithms to find the Max path sum between two nodes in Binary Tree along with time and space complexity.

Table of Contents
1) Introduction
2) Naive approach
3) Optimized approach
4) Conclusion

1) Introduction

A path in a binary tree is a sequence of consecutive nodes.

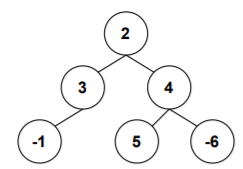
Consider the above binary tree, few of the paths are listed below

-1->3->2->4->5
-1->3->2->4->-6
5->4->-6
3->2->4

Among all the paths, 3->2->4->5 has the maximum sum

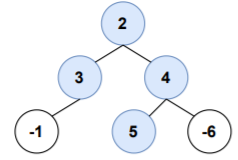
A path with maximum sum need not pass through the root node always.

Consider the following graph

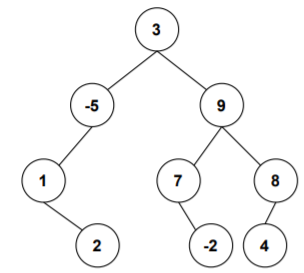
The maximum sum path doesn't pass through the root node.

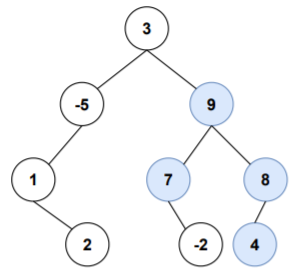
Let's look at ways to solve this.

2) Naive approach

For each node in the binary tree, traverse through the left sub-tree of the node and find the maximum sum path with left child of the node as starting node and similarly traverse through the right sub-tree of the node and find the maximum sum path with right child of the node as starting node. Combine the path sums with node's value to get current node's max path sum. Keep track of max path sum.

Implementation

class TreeNode:
    def __init__(self,val):
        self.val=val
        self.left=None
        self.right=None
def findMax(root,currPathSum):
    global maxValue
    maxValue=max(maxValue,currPathSum)
    if root is None:
        return
    findMax(root.left,currPathSum+root.val)
    findMax(root.right,currPathSum+root.val)
def traverse(root):
    global maxValue,maxPathSum
    if root==None:
        return
    maxValue=float('-inf')
    findMax(root.left,0)
    leftMaxPathSum=max(maxValue,0)
    maxValue=float('-inf')
    findMax(root.right,0)
    rightMaxPathSum=max(maxValue,0)
    maxPathSum=max(maxPathSum,root.val+leftMaxPathSum+rightMaxPathSum)
    traverse(root.left)
    traverse(root.right)
maxPathSum=float('-inf')
root=TreeNode(3)
root.left=TreeNode(-5)
root.right=TreeNode(9)
root.left.left=TreeNode(1)
root.right.left=TreeNode(7)
root.right.right=TreeNode(8)
root.left.left.right=TreeNode(2)
root.right.left.right=TreeNode(-2)
root.right.right.left=TreeNode(4)
traverse(root)
print(maxPathSum)

Output:

28

The time complexity for the above approach is O(N²), where N is the number of nodes in the binary tree, as for each node we traverse the left sub-tree and right sub-tree of that node hence O(N*N). The problem can be solved in O(N) time complexity. Let's look at the optimized approach.

3) Optimized approach

This is a bottom-up approach.

We start by exploring the bottom nodes i.e., leaf nodes and then explore the nodes above them and this process continues (post-order fashion).

For each node while we explore there're some condition to consider.Let's look at them

For calculating maximum path sum that can be obtained for a particular node there are four possibilities:

Let leftMaxPathSum = maximum path sum obtained with left child as starting node
   rightMaxPathSum = maximum path sum obtained with right child as starting node

1.Consider only node's value

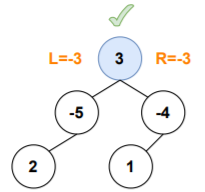
Here, leftMaxPathSum<0 and rightMaxPathSum<0, if any of these is included then the sum will be decreased futher.Hence, the maximum path sum obtained for the node will be the node's value itself.

2.Consider node's value + leftMaxPathSum

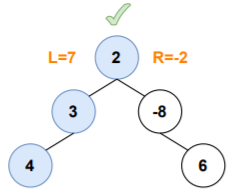
Here, leftMaxPathSum>0 and rightMaxPathSum<0, include only the leftMaxPathSum as it will contribute in increasing the value of maximum path sum obtained for the node.

3.Consider node's value + rightMaxPathSum

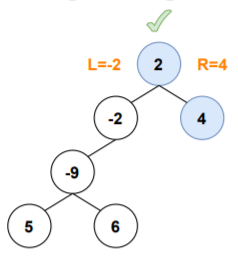
Here, leftMaxPathSum<0 and rightMaxPathSum>0, include only the rightMaxPathSum as it will contribute in increasing the value of maximum path sum obtained for the node.

4.Consider node's value + leftMaxPathSum + rightMaxPathSum

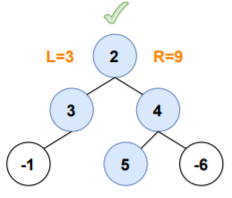
Here, leftMaxPathSum>0 and rightMaxPathSum>0, both leftMaxPathSum and rightMaxPathSum can included as they both will contribute in increasing the value of maximum path sum obtained for the node.

In this approach each node returns a value which is the max path sum with it as the starting node.

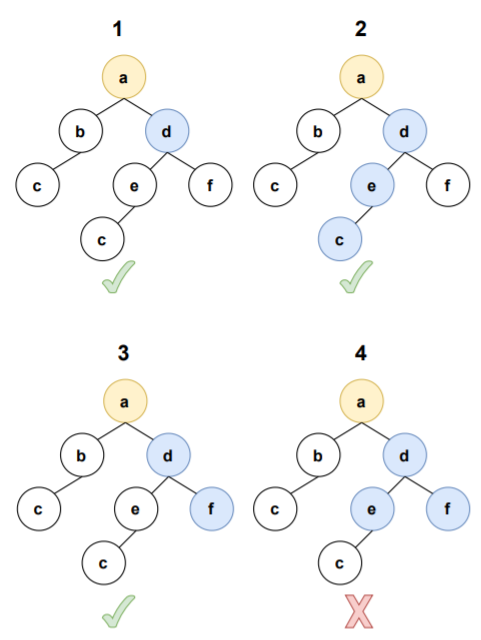
In the above diagrams assume that we are processing node 'd'.

As per the numbering,

1 indicates returning node's value itself
2 indicates returning node's value + leftMaxPathSum
3 indicates returning node's value + rightMaxPathSum
4 indicates returning node's value + leftMaxPathSum + rightMaxPathSum

From the diagrams it can be seen that in cases 1,2,3 the paths a-d, a-d-e-c, a-d-f are valid but in 4 there is no clear path.Hence, case 4 doesn't come into consideration while returning.

Hence, there are three possibilities for returning:

1. node's value
2. node's value + leftMaxPathSum
3. node's value + rightMaxPathSum

Return the value which ever is the highest.

ALGORITHM

1.Visit each node in post-order fashion.
2.If there's no left child for a node then leftMaxPathSum would be 0 else leftMaxPathSum would be the value returned by left child of the node
3.Similary if there's no right child for a node then rightMaxPathSum would be 0 else rightMaxPathSum would be the value returned by right child of the node.
4.Take various values into variables for simplicity
   w=node's value
   x=node's value + leftMaxPathSum
   y=node's value + rightMaxPathSum
   z=node's value + leftMaxPathSum + rightMaxPathSum
5.The current node's maximum path sum value is
   currMaxPathSum=max(w,x,y,z)
6.Update the maxPathSum as follows
   maxPathSum=max(maxPathSum,currMaxPathSum)
7.Return max sum path with the current node as starting node as follows
   return max(w,x,y)

Let's understand the algorithm through an example.

Let maxPathSum be the maximum path sum

Initialize maxPathSum=-infinity

For 2

leftMaxPathSum=0
rightMaxPathSum=0
w=2
x=2+0=2
y=2+0=2
z=2+0+0=2
currMaxPathSum=max(w,x,y,z)
        =max(2,2,2,2)
        =2
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(-infinity,2)
      =2
return value=max(w,x,y)
      =max(2,2,2)
      =2

For -2

leftMaxPathSum=0
rightMaxPathSum=0
w=-2
x=-2+0=-2
y=-2+0=-2
z=-2+0+0=-2
currMaxPathSum=max(w,x,y,z)
        =max(-2,-2,-2,-2)
        =-2
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(2,-2)
      =2
return value=max(w,x,y)
      =max(-2,-2,-2)
      =-2

For 4

leftMaxPathSum=0
rightMaxPathSum=0
w=4
x=4+0=4
y=4+0=4
z=4+0+0=4
currMaxPathSum=max(w,x,y,z)
        =max(4,4,4,4)
        =4
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(2,4)
      =4
return value=max(w,x,y)
      =max(4,4,4)
      =4

For 1

leftMaxPathSum=0
rightMaxPathSum=2
w=1
x=1+0=1
y=1+2=3
z=1+0+2=3
currMaxPathSum=max(w,x,y,z)
        =max(1,1,3,3)
        =3
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(4,3)
      =4
return value=max(w,x,y)
      =max(1,1,3)
      =3

For 7

leftMaxPathSum=0
rightMaxPathSum=-2
w=7
x=7+0=7
y=7+(-2)=5
z=7+0+(-2)=5
currMaxPathSum=max(w,x,y,z)
        =max(7,7,5,5)
        =7
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(4,7)
      =7
return value=max(w,x,y)
      =max(7,7,5)
      =7

For 8

leftMaxPathSum=4
rightMaxPathSum=0
w=8
x=8+4=12
y=8+0=8
z=8+4+0=12
currMaxPathSum=max(w,x,y,z)
        =max(8,12,8,12)
        =12
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(7,12)
      =12
return value=max(w,x,y)
      =max(8,12,8)
      =12

For -5

leftMaxPathSum=3
rightMaxPathSum=0
w=-5
x=(-5)+3=-2
y=(-5)+0=-5
z=(-5)+3+0=-2
currMaxPathSum=max(w,x,y,z)
      =max(-5,-2,-5,-2)
      =-2
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(12,-2)
      =12
return value=max(w,x,y)
      =max(-5,-2,-5)
      =-2

For 9

leftMaxPathSum=7
rightMaxPathSum=12
w=9
x=9+7=16
y=9+12=21
z=9+7+12=28
currMaxPathSum=max(w,x,y,z)
        =max(9,16,21,28)
        =28
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(12,28)
      =28
return value=max(w,x,y)
      =max(9,16,21)
      =21

For 3

leftMaxPathSum=-2
rightMaxPathSum=21
w=3
x=3+(-2)=1
y=3+21=24
z=3+(-2)+21=22
currMaxPathSum=max(w,x,y,z)
        =max(3,1,24,22)
        =24
maxPathSum=max(maxPathSum,currMaxPathSum)
      =max(28,24)
      =28
return value=max(w,x,y)
      =max(3,1,24)
      =24

Let's represent the obtained values diagramatically,

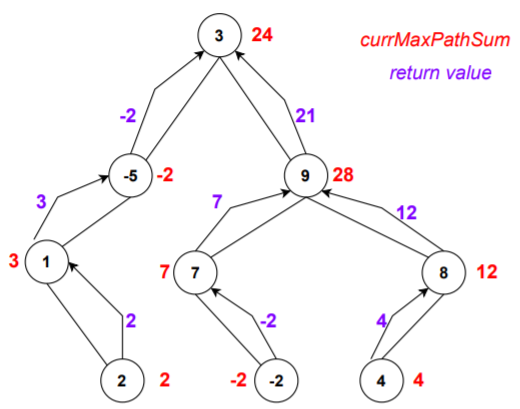
Hence, the maximum path sum obtained is 28.

Implementation

class TreeNode:
    def __init__(self,val):
        self.val=val
        self.left=None
        self.right=None
def findMaxPathSum(root):
    global maxPathSum
    if root==None:
        return 0
    leftMaxPathSum=findMaxPathSum(root.left)
    rightMaxPathSum=findMaxPathSum(root.right)
    w=root.val
    x=root.val+leftMaxPathSum
    y=root.val+rightMaxPathSum
    z=root.val+leftMaxPathSum+rightMaxPathSum
    currMaxPathSum=max(w,x,y,z)
    maxPathSum=max(maxPathSum,currMaxPathSum)
    return max(w,x,y)
maxPathSum=float('-inf')
root=TreeNode(3)
root.left=TreeNode(-5)
root.right=TreeNode(9)
root.left.left=TreeNode(1)
root.right.left=TreeNode(7)
root.right.right=TreeNode(8)
root.left.left.right=TreeNode(2)
root.right.left.right=TreeNode(-2)
root.right.right.left=TreeNode(4)
findMaxPathSum(root)
print(maxPathSum)

28

4) Conclusion

The optimized approach takes O(N),where N is the number of nodes in the binary tree, time complexity as the tree is traversed only once.

With this article at OpenGenus, you must have the complete idea of finding the Max path sum between two nodes in Binary Tree.