Find Mother Vertex in a Graph【O(V+E)】

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 30 minutes

What is Mother Vertex?
A mother vertex in a graph is a vertex from which we can reach all the nodes in the graph through directed path. In other words, A mother vertex in a graph G = (V,E) is a vertex v such that all other vertices in G can be reached by a path from v.

Example:

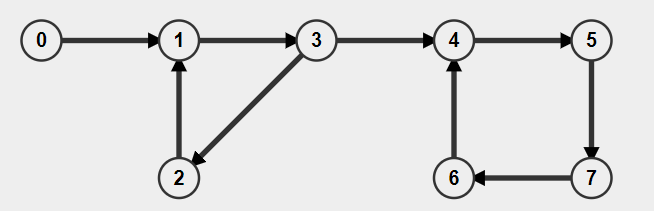
Consider the following Graph:

Graph2

Vertices reachable from vertex 0:
0 -> 1 -> 3 -> 2 -> 4 -> 5 -> 7 -> 6

Vertices reachable from vertex 1:
1 -> 3 -> 2 -> 4 -> 5 -> 7 -> 6

Vertices reachable from vertex 2:
2 -> 1 -> 3 -> 4 -> 5 -> 7 -> 6

Vertices reachable from vertex 3:
3 -> 2 -> 1 -> 4 -> 5 -> 7 -> 6

Vertices reachable from vertex 4:
4 -> 5 -> 7 -> 6

Vertices reachable from vertex 5:
5 -> 7 -> 6 -> 4

Vertices reachable from vertex 6:
6 -> 4 -> 5 -> 7

Vertices reachable from vertex 7:
7 -> 6 -> 4 -> 5

The vertex from which all other vertices are reachable: 0

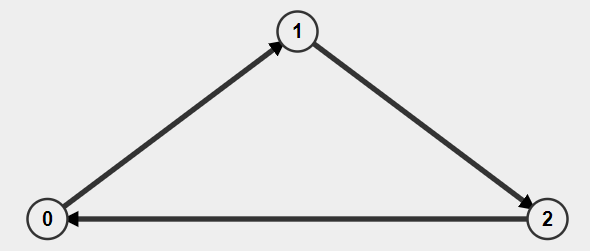
There can be more than one mother vertices in a graph. We need to output anyone of them.For Example,in the below graph, vertices 0, 1 and 2 are mother vertices.

Graph3

How to find mother vertex?

Case 1:- Undirected Connected Graph : In this case, all the vertices are mother vertices as we can reach to all the other nodes in the graph.
Case 2:- Undirected/Directed Disconnected Graph : In this case, there is no mother vertx as we cannot reach to all the other nodes in the graph from a vertex.
Case 3:- Directed Connected Graph : In this case, we have to find a vertex -v in the graph such that we can reach to all the other nodes in the graph through a directed path.

A simple approach

A trival approach will be to perform DFS on all the vertices and find whether we can reach all the nodes in the graph.Below is the code for this.

// C++ program to find the mother vertex in a graph
#include<iostream> 
#include<list> 
using namespace std; 
  
// Graph class represents a directed graph 
// using adjacency list representation 
class Graph 
{ 
    int V;    // No. of vertices 
    
    
    // Pointer to an array containing 
    // adjacency lists 
    list<int> *adj; 
  
    // A recursive function used by DFS 
    void DFSUtil(int v, bool visited[]); 
public: 
    Graph(int V);   // Constructor 
  
    // function to add an edge to graph 
    void addEdge(int v, int w); 
    
    int visitedNodes; //Number of visited nodes
    
    // DFS traversal of the vertices 
    // reachable from v 
    void DFS(int v); 
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
    adj = new list<int>[V]; 
} 
  
void Graph::addEdge(int v, int w) 
{ 
    adj[v].push_back(w); // Add w to v’s list. 
} 
  
void Graph::DFSUtil(int v, bool visited[]) 
{ 
    // Mark the current node as visited and 
    // print it 
    visited[v] = true;
    visitedNodes++;
  
    // Recur for all the vertices adjacent 
    // to this vertex 
    list<int>::iterator i; 
    for (i = adj[v].begin(); i != adj[v].end(); ++i) 
        if (!visited[*i]) 
            DFSUtil(*i, visited); 
} 
  
// DFS traversal of the vertices reachable from v. 
// It uses recursive DFSUtil() 
void Graph::DFS(int v) 
{ 
    // Mark all the vertices as not visited 
    visitedNodes=0;
    bool *visited = new bool[V]; 
    for (int i = 0; i < V; i++) 
        visited[i] = false; 
  
    // Call the recursive helper function 
    // to print DFS traversal 
    DFSUtil(v, visited); 
} 
  
// Driver code 
int main() 
{ 
    Graph g(8);
    int i;
    int a[] = {0,1,2,3,4,5,6,7};
    g.addEdge(0,1);
    g.addEdge(1, 3); 
	g.addEdge(2, 1); 
	g.addEdge(3, 2); 
	g.addEdge(3, 4); 
	g.addEdge(4, 5); 
	g.addEdge(6, 4);
	g.addEdge(5,7);
	g.addEdge(7,6);
    int n=sizeof(a)/sizeof(a[0]);
    
    //checking for each the vertex how nodes are reachable.
    for(i=0;i<n;i++){
        g.DFS(a[i]);
        
        //If the vertex can reach all the other vertices then it is the mother vertex
       if(g.visitedNodes==n)
           break;
    }
    if(i==n)
        cout<<"There is no mother vertex in this graph";
    else
        cout<<"Mother vertex of this graph is "<<a[i];
  
    return 0;  
}

Output:

Mother vertex of this graph is 0

The time complexity for this approach is O(V(V+E)),which is very inefficient for large graphs where V=Number of vertices and E=Number of edges

Better approach

The mother vertex can be found in O(V+E) time complexity. In a graph of strongly connected components, mother vertices are always vertices of source component in component graph. The idea is based on below fact.
If there exist mother vertex (or vertices), then one of the mother vertices is the last finished vertex in DFS. (Or a mother vertex has the maximum finish time in DFS traversal).

A vertex is said to be finished in DFS if a recursive call for its DFS is over, i.e., all descendants of the vertex have been visited.

Lets prove above statements.Let the last finished vertex be v. Basically, we need to prove that there cannot be an edge from another vertex u to v if u is not another mother vertex (Or there cannot exist a non-mother vertex u such that u-→v is an edge). There can be two possibilities.

Recursive DFS call is made for u before v. If an edge u-→v exists, then v must have finished before u because v is reachable through u and a vertex finishes after all its descendants.
Recursive DFS call is made for v before u. In this case also, if an edge u-→v exists, then either v must finish before u (which contradicts our assumption that v is finished at the end) OR u should be reachable from v (which means u is another mother vertex).

Algorithm:

Do the DFS travsersal of the give graph. and keep the track of last finished vertex 'v'.
Then check v is the mother vertex of the given graph by doing DFS.If v is not the mother vertex then there does not exist the mother vertex in graph.

Below is implementation of above algorithm.

// C++ program to find the mother vertex
#include<iostream> 
#include<list> 
using namespace std;  
  
// Graph class represents a directed graph 
// using adjacency list representation 
class Graph 
{ 
    int V;    // No. of vertices  
    
    // Pointer to an array containing 
    // adjacency lists 
    list<int> *adj; 
  
    // A recursive function used by DFS 
    void DFSUtil(int v, bool visited[]); 
public: 
    Graph(int V);   // Constructor 
  
    // function to add an edge to graph 
    void addEdge(int v, int w); 
    int FindMotherVertex();
    
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
    adj = new list<int>[V]; 
} 
  
void Graph::addEdge(int v, int w) 
{ 
    adj[v].push_back(w); // Add w to v’s list. 
} 
  
void Graph::DFSUtil(int v, bool visited[]) 
{ 
    // Mark the current node as visited
    visited[v] = true;
  
    // Recur for all the vertices adjacent 
    // to this vertex 
    list<int>::iterator i; 
    for (i = adj[v].begin(); i != adj[v].end(); ++i) 
        if (!visited[*i]) 
            DFSUtil(*i, visited); 
} 
  
// DFS traversal of the vertices reachable from v. 
// It uses recursive DFSUtil() 
int Graph::FindMotherVertex() 
{ 
    // Mark all the vertices as not visited 
    bool *visited = new bool[V]; 
    for (int i = 0; i < V; i++) 
        visited[i] = false;
    
    int v=0; //for last finished vertex
    
    //To find the last finished vertex
    for(int i=0;i<V;i++){
        if(!visited[i]){
            DFSUtil(i,visited);
            v=i;
        }
    }
    
    //Checking if the v is the  mother vertex if all the nodes are 
    //reachable then return v otherwise return -1 no mother vertex present
    for (int i = 0; i < V; i++) 
        visited[i] = false;
        
    DFSUtil(v,visited);
    for(int i=0;i<V;i++)
        if(!visited[i])
            return -1;
    return v;
} 
  
// Driver code 
int main() 
{ 
    Graph g(8);
    int i;
    g.addEdge(0,1);
    g.addEdge(1, 3); 
	g.addEdge(2, 1); 
	g.addEdge(3, 2); 
	g.addEdge(3, 4); 
	g.addEdge(4, 5); 
	g.addEdge(6, 4);
	g.addEdge(5,7);
	g.addEdge(7,6);
	
    i=g.FindMotherVertex();
    if(i==-1)
        cout<<"There is no mother vertex in this graph";
    else
        cout<<"Mother vertex of this graph is "<<i;
  
    return 0; 
}

Output:

Mother vertex of this graph is 0

Time Complexity: O(V+E)

Find Mother Vertex in a Graph【O(V+E)】

Algorithms Graph Algorithms depth first search

How to find mother vertex?

A simple approach

Better approach

Different types of Autoencoders

Working with Clipboard API and events in HTML