
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
You are given a directed graph and two vertices on it. Your task is to find if there exists a path between the first vertex to the second vertex or not.
Example
Consider the following graph:
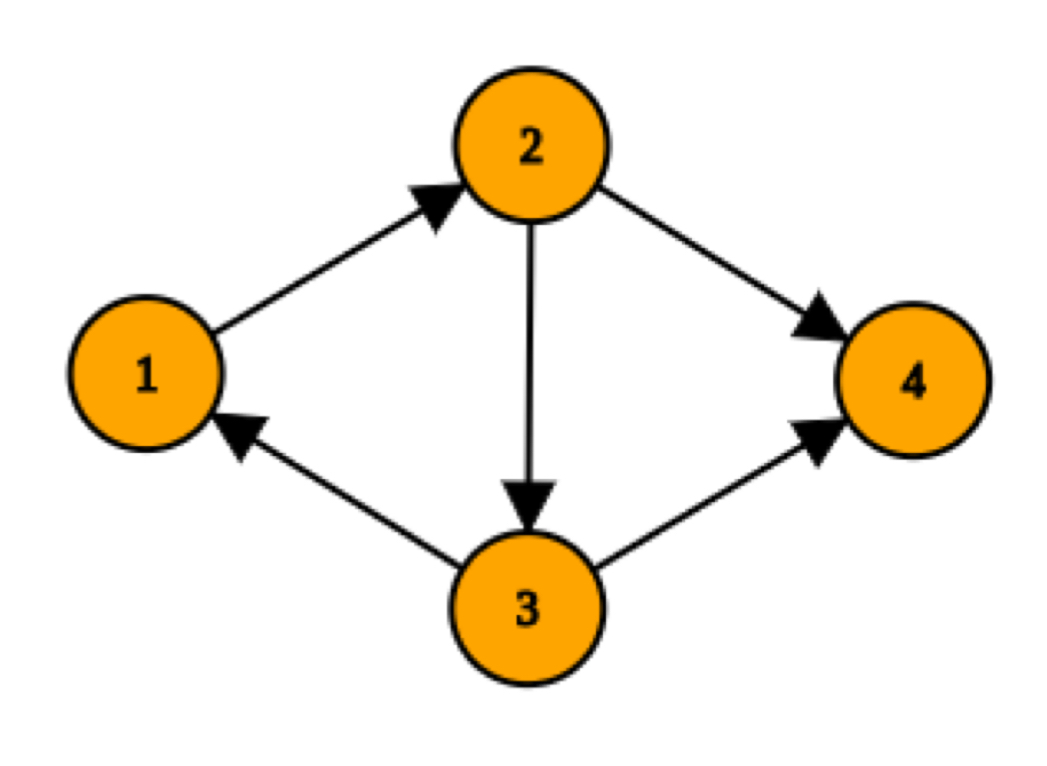
Input to construct the above graph:
Input:
No. of nodes in graph = 4
No. of edges in graph = 5
Edges:
1 2
2 3
2 4
3 1
3 4
No. of queries = 2
1 4
4 2
Output:
Yes
No
Explanation:
For the first query, the answer is Yes because we can construct a path as shown in the diagram below ( 1->2->4 ) but for the second query the answer is No because there are no outgoing edges from vertex four.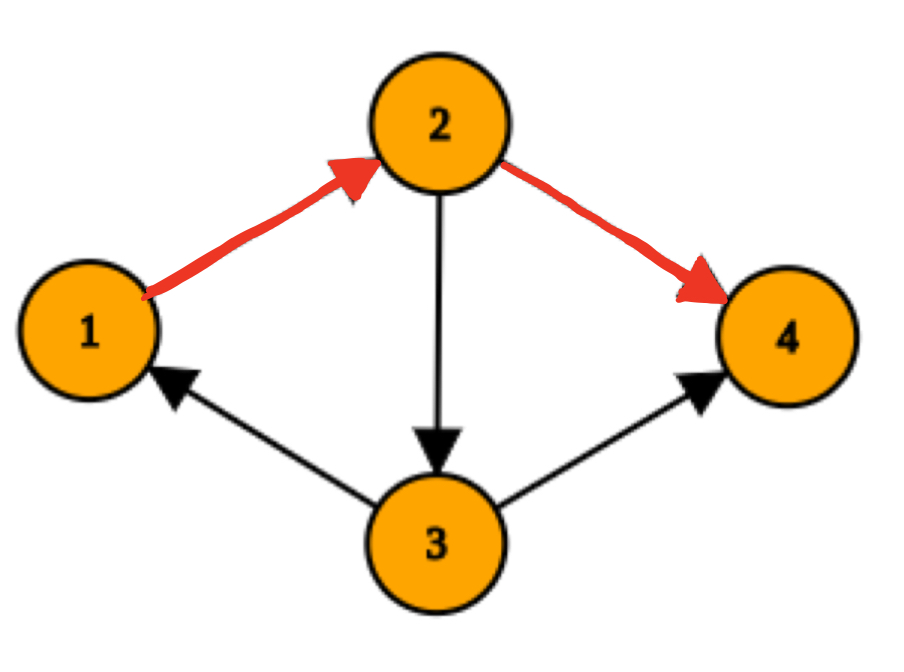
Approach
To solve this problem, we can use either BFS (Breadth First Search) or DFS (Depth First Search) to find if there exists a path between two vertices.
Some important points:
1. For representing nodes we will use 1-indexing or in other words the nodes will be numbered from 1 to number_of_nodes.
2. To represent the graph we will use a 2-D vector in C++ and we will use the adjacency list representation as it gives us lower time and space complexity. We will resize the 2-D vector to contain vectors equal to no. of nodes.
std::vector <std::vector<int>> graph;
graph.resize(number_of_nodes);
1. Using BFS
Here we will use Breadth First Search in the solution. Take the first vertex as the source in BFS and if the second vertex is found in traversal print Yes otherwise No.Pseudocode
isPathBFS(Graph G, node source, node end):
Queue Q
Q.enqueue( source ) //add the source node to the queue first
tag source as visited
while (Q is not empty):
v = Q.dequeue( )
for all neighbours w of v in Graph G
if w is end :
return true
if w is not visited :
Q.enqueue( w )
tag w as visited
return false
Example
In the Graph G in the image below, we find whether there exists a path between node 1 and node 6 using BFS. To find if there exists such a path, we will use BFS with node 1 as our source and check if node 6 exists in our traversal.Step 1
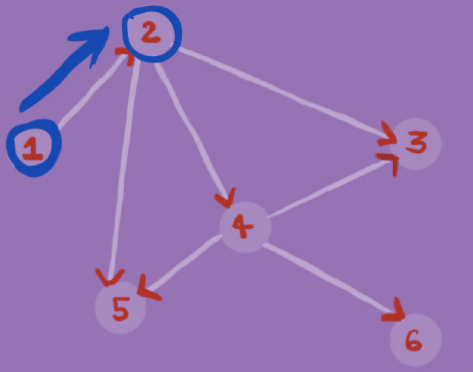
Step 2
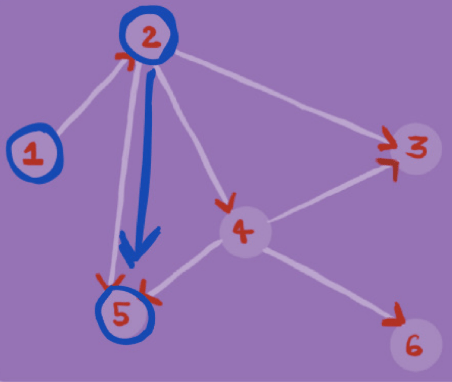
Step 3

Step 4
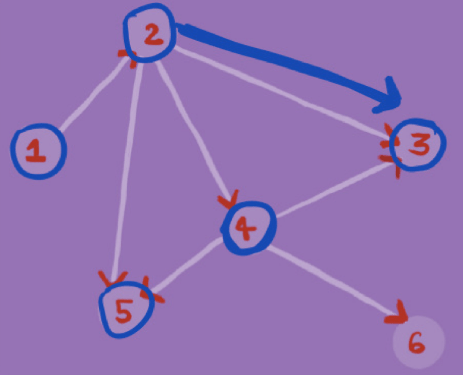
Step 5
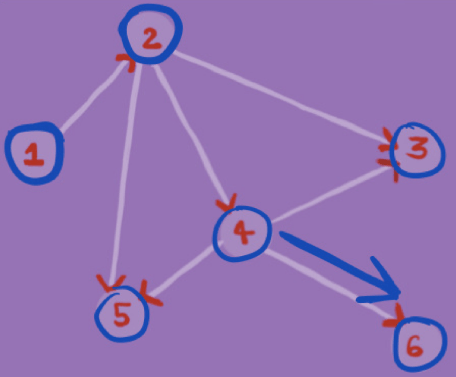
As node 6 is in our traversal ( BFS ), therefore we can draw a path from node 1 to node 6. ( 1->2->4->6 )
Solution using BFS
- C++
C++
// C++ program to check if there exists a path between two vertices of a graph.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
//function definition
bool isPathBFS(vector <vector<int>>& graph, int nodes, int source, int end){
//BFS implementation
bool visited[nodes];
for(int i = 0;i<nodes;++i){
visited[i] = false;
}
queue <int> traversal;
traversal.push(source);
visited[source-1] = true;
while(!traversal.empty()){
//dequeue the front element
source = traversal.front();
traversal.pop();
for(int i = 0;i < (int)graph[source-1].size();++i){
if(graph[source-1][i]==end)
return true;
if(visited[graph[source-1][i]-1]==false){
traversal.push(graph[source-1][i]);
visited[graph[source-1][i]-1] = true;
}
}
}
return false;
}
int main(){
//input
int nodes;
cout << "No. of nodes in graph = ";
cin >> nodes;
int edges;
cout << "No. of edges in graph = ";
cin >> edges;
vector <vector<int>> graph;
graph.resize(nodes);
cout << "Edges:\n";
int source,end;
while(edges--){
cin >> source>>end;
//As we are using 1-indexing for nodes
if(source > nodes || end > nodes){
cout << "Invalid nodes.";
return 1;
}
graph[source-1].push_back(end);
}
int query;
cout << "No. of queries = ";
cin >> query;
while(query--){
cin >> source>>end;
//output
if(source > nodes || end > nodes){
cout << "Invalid nodes.\n";
continue;
}
if(isPathBFS(graph,nodes,source,end)){
cout << "Yes"<<"\n";
}else cout << "No"<<"\n";
}
return 0;
}
Time Complexity ( for adjancency list representation )
- Worst case time complexity:
O(V+E) - Best case time complexity:
Ω(1) - Space complexity:
O(V+E)
2. Using DFS
Here we will use Depth First Search in the solution. Take the first vertex as the source in DFS and if the second vertex is found in traversal print Yes otherwise No.Pseudocode
isPathDFS(Graph G, node source, node end):
Stack S
S.push( source )
tag source as visited
while(S is not empty):
v = S.top()
S.pop()
for all neighbours of w of v in Graph G:
if w is end :
return true
if w is not visited :
S.push( w )
tag w as visited
return false
Example
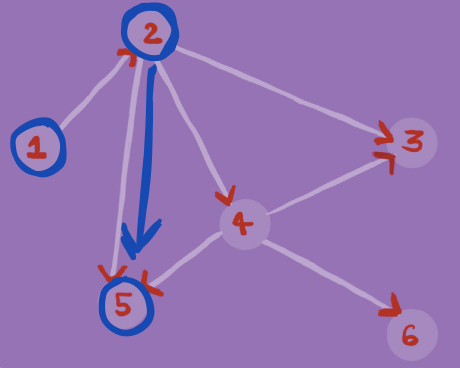
In the Graph G in the image below, we find whether there exists a path between node 1 and node 6 using DFS. To find if there exists such a path, we will use DFS with node 1 as our source and check if node 6 exists in our traversal.Step 1
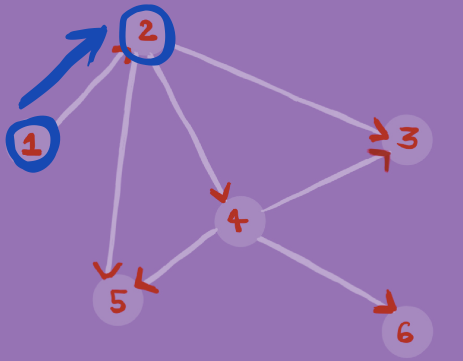
Step 2
Step 3
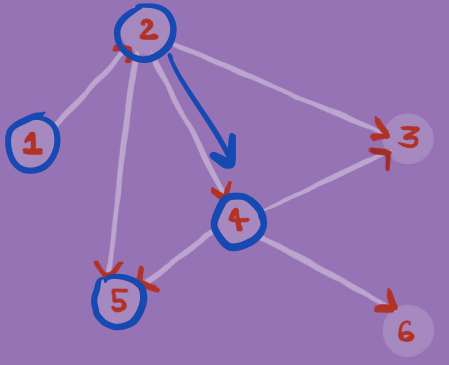
Step 4

As node 6 is in our traversal ( DFS ), therefore we can draw a path from node 1 to node 6. ( 1->2->4->6 )
Solution using DFS
- C++
C++
// C++ program to check if there exists a path between two vertices of a graph.
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
//function definition
bool isPathDFS(vector <vector<int>>& graph, int nodes, int source, int end){
//DFS implementation
bool visited[nodes];
for(int i = 0;i<nodes;++i){
visited[i] = false;
}
stack <int> traversal;
traversal.push(source);
visited[source-1] = true;
while(!traversal.empty()){
//Pop the front element
source = traversal.top();
traversal.pop();
for(int i = 0;i < (int)graph[source-1].size();++i){
if(graph[source-1][i]==end)
return true;
if(visited[graph[source-1][i]-1]==false){
traversal.push(graph[source-1][i]);
visited[graph[source-1][i]-1] = true;
}
}
}
return false;
}
int main(){
//input
int nodes;
cout << "No. of nodes in graph = ";
cin >> nodes;
int edges;
cout << "No. of edges in graph = ";
cin >> edges;
vector <vector<int>> graph;
graph.resize(nodes);
cout << "Edges:\n";
int source,end;
while(edges--){
cin >> source>>end;
//As we are using 1-indexing for nodes
if(source > nodes || end > nodes){
cout << "Invalid nodes.";
return 1;
}
graph[source-1].push_back(end);
}
int query;
cout << "No. of queries = ";
cin >> query;
while(query--){
cin >> source>>end;
//output
if(source > nodes || end > nodes){
cout << "Invalid nodes.\n";
continue;
}
if(isPathDFS(graph,nodes,source,end)){
cout << "Yes"<<"\n";
}else cout << "No"<<"\n";
}
return 0;
}
Time Complexity ( for adjancency list representation )
- Worst case time complexity:
O(V+E) - Best case time complexity:
Ω(1) - Space complexity:
O(V+E)
Tradeoffs between BFS and DFS approach
BFS can be useful to find the minimum number of edges between two nodes while DFS may not always give us the path with minimum number of edges as it may traverse one adjacent node very deeply before going to other neighbouring nodes (as BFS works level by level while DFS works depth wise).For other differences between BFS vs DFS refer to the article : BFS vs DFS
Exercise: Modify the above algorithm to find any path between two vertices if it exists.
Also feel free to share your approach in the discussion thread below. Happy Coding :)
