Find and print all the paths between two vertices in a graph【O((2^V)*(V+E))】

Reading time: 30 minutes | Coding time: 10 minutes

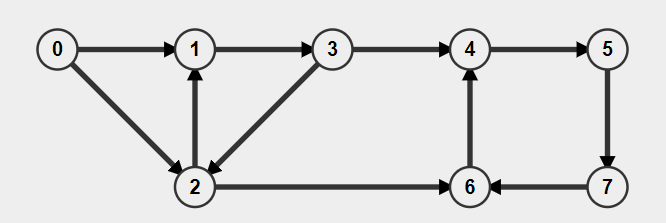
Given a directed graph, a vertex ‘v1’ and a vertex ‘v2’, print all paths from given ‘v1’ to ‘v2’.Consider the following directed graph. Let the v1 be 0 and v2 be 6. There are 4 different paths from 0 to 6.

Below are the paths between 0 and 6:
0->1->3->2->6
0->1->3->4->5->7->6
0->2->1->3->4->5->7->6
0->2->6

How to find path between two vertex?

• Case 1:- Undirected Connected Graph : In this case, always a path exist between given two vertices
• Case 2:- Undirected/Directed Disconnected Graph : In this case, There is no path between between Disconnected vertices
• Case 3:- Directed Connected Graph : In this case, we have to check whether path exist between the given two vertices or not

The idea is to do Depth First Traversal of given directed graph. Start the traversal from 'v1'. Keep storing the visited vertices in an array say ‘path[]’. If we reach the vertex 'v2', pathExist becomes true and print contents of path[]. The important thing is to mark current vertices in path[] as visited also, so that the traversal doesn’t go in a cycle. If there is no path exist between the vertices then pathExist remains false.

Approach: Use Depth First Search

1. Mark all the nodes as unvisited and create and empty path and make the pathExist false.
2. Start from the vertex v1 and visit the next vertex (use adjacency list).
3. Keep track of visited nodes to avoid cycles.
4. Add current vertex to result (taking integer array here) to keep track of path from vertex v1.
5. Now if you look carefully, the new problem is to find paths from the current vertex to destination. For instance as per the example above, start from vertex 0 and visit vertex 1. Now all the paths from vertex 1 to vertex 5 will be included in our final result if we add vertex 0. So make a recursive call with source as vertex 1 and destination as vertex 5.
6. Once reach to the destination vertex, print the path.
7. Mark the current node as unmarked and delete it from path.
8. Now visit the next node in adjacency list in step 1 and repeat all the steps (loop)

Implementation

Following is C++ implementation of above approach.

# // C++ program to print the paths between two vertices
#include<iostream> 
#include<list> 
using namespace std;  
  
// Graph class represents a directed graph 
// using adjacency list representation 
class Graph 
{ 
    int V;    // No. of vertices  
    // Pointer to an array containing 
    // adjacency lists 
    list<int> *adj; 
  
    // A recursive function used by printAllPaths()
    void printAllPathsUtil(int v1, int v2, bool visited[], int path[], int index); 
public: 
    Graph(int V);   // Constructor 
    bool pathExist; //variable to indicate if path exist or not
    // function to add an edge to graph 
    void addEdge(int v, int w); 
    void printAllPaths(int v1, int v2);
    
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
    adj = new list<int>[V]; 
} 
  
void Graph::addEdge(int v, int w) 
{ 
    adj[v].push_back(w); // Add w to v’s list. 
} 

// A recursive function to print all paths from 'v1' to 'v2'. 
// visited[] keeps track of vertices in current path. 
// path[] stores actual vertices and index is current 
// index in path[] 
void Graph::printAllPathsUtil(int v1, int v2, bool visited[], int path[], int index) 
{ 
    // Mark the current node as visited and store it in path[] 
    visited[v1] = true;
    path[index]=v1;
    index++;
    // If current vertex is same as v2, then print 
	// current path[] 
    if(v1==v2){
        int i;
        if(!pathExist)
            cout<<"Following are the paths between "<<path[0]<<" and "<<path[index-1]<<endl;
        pathExist=true;
        for(i=0;i<index-1;i++)
            cout<<path[i]<<"->";
        cout<<path[i]<<endl;
    }
    else{ // If current vertex is not v2 
    // Recur for all the vertices adjacent 
    // to this vertex 
        list<int>::iterator i; 
        for (i = adj[v1].begin(); i != adj[v1].end(); ++i) 
            if (!visited[*i]) 
                printAllPathsUtil(*i, v2, visited, path, index); 
    }
    // Remove current vertex from path[] and mark it as unvisited 
    index--;
    visited[v1]=false;
} 
  
// DFS traversal of the vertices reachable from v. 
// It uses recursive prinAllPathsUtil 
void Graph::printAllPaths(int v1, int v2) 
{ 
    // Mark all the vertices as not visited 
    bool *visited = new bool[V]; 
    for (int i = 0; i < V; i++) 
        visited[i] = false;
        
    // Create an array to store paths 
    int *path = new int[V];
    
    // Initialize path[] as empty 
    int index = 0;
    
    pathExist=false;
    
    // Call the recursive helper function to print all paths 
    printAllPathsUtil(v1,v2,visited,path,index);
    
   
} 
  
// Driver code 
int main() 
{
    // Create a graph given in the above diagram
    Graph g(8);
    g.addEdge(0,1);
    g.addEdge(1, 3); 
	g.addEdge(2, 1); 
	g.addEdge(3, 2); 
	g.addEdge(3, 4); 
	g.addEdge(4, 5); 
	g.addEdge(6, 4);
	g.addEdge(5,7);
	g.addEdge(7,6);
	g.addEdge(0,2);
	g.addEdge(2,6);
	int v1=0, v2=6;
	g.printAllPaths(v1,v2);
	if(!g.pathExist){
	    cout<<"There is no path exist between "<<v1<<" and "<<v2;
	}
    return 0; 
} 

Output:

Following are the paths between 0 and 6
0->1->3->2->6
0->1->3->4->5->7->6
0->2->1->3->4->5->7->6
0->2->6

Example:

• printAllthePaths() function initialize visited array mark all the node as unvisited and creates an empty path error and initially path exist is false than is call the printAllthePathsUtil() the helper function.
• printAllthePathsUtil() simply do the DFS from the given vertex goto vertices which are reachable from given vertex.
• Let's Take an example all the paths from 0 to 6.
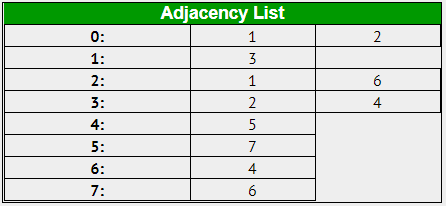
• Below is the adjacency list of all the vertex for reference
  
• start the DFS from vertex 0 mark the current vertex 0 as visited and add it to path[] array so now path[] array contains one element 0 and increase the path index.now we will check the current vertex 0 is the destination vertex 6,No,it is not so we go into the adjacency list(It list which contains information about the connections of current vertex) of vertex 0 we which contains 1 and 2.check vertex 1 is visited no go the vertex 1.
  
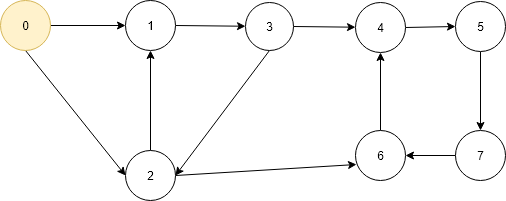
• Now it is new problem of finding path from 1 to 6 so we call the function again.
• Now current vertex is 1 so it is marked As visited marked as visited now the two vertices are marked as visited. store the current vertex 1 into path[] so it contains two elements 0 and 1 increase the path index and check it is the destination vertex 6 No then go to adjacency list of vertex 1 which contains 3.Check vertex 3 is visited no go to the vertex 3.
  
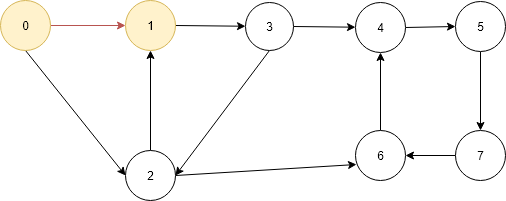
• again it is new problem finding path from 3 to 6.
• Now current vertex is 3 same as above two vertex mark it as visited now visited now there are three 3 visited vertices 0, 1 and 3 and add to the path[] so now it contains three elements 0, 1 and 3. check if it is destination vertex no the go to the adjacency list of vertex 3 which contains 2 and 4.check vertex 2 is visited no go to vertex 2.
  
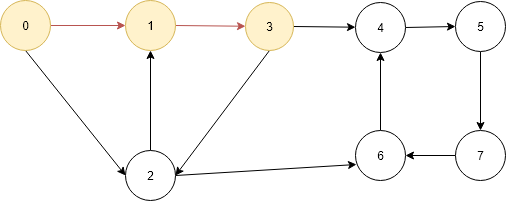
• again it is same problem finding path from 2 to 6 so we call the printAllthePathsUtil() function recursively.
• Now the current vertex is 2 same as above mark it as visited so now there are 4 elements marked as visited 0, 1, 3 and 2.Add to the path[] so now it contains four elements 0, 1, 3 and 2 and check if is destination vertex no then go to the adjacency list of vertex 2 which contains 1 and 6.
  
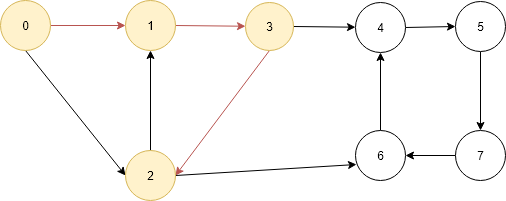
• Now check vertex 1 is visited then go the another element in the list which vertex 6 which is not visited.
• Now the current vertex is 6 so do same as above marked it as visited and add to the path[] so now is contains 0, 1, 3, 2 and 6.Check the current vertex 6 is the destination vertex yes then make the pathExist true and print path[].
  
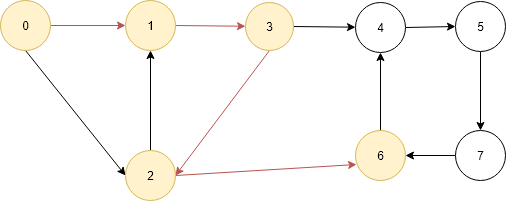
• There can be one then more path exist between two nodes so we have to backtrack so we mark the current vertex 6 as not visited and delete it from path[].And return to the step where it is called.
  
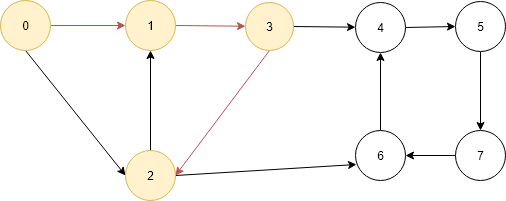
• Now there is no more elements into the adjacency list of vertex 2 and same as above mark the vertex 2 as not visited and delete it from path[].
  
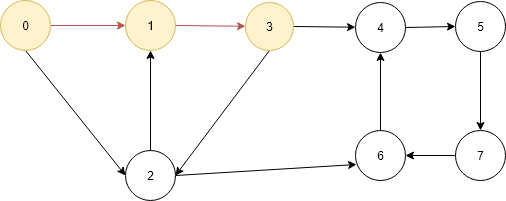
• Now again return to the vertex 3 and another element of adjacency list of vertex 3 i.e. vertex 4 as vertex 4 is not visited go to the vertex 4.
• It is same above call the function again for finding path between vertex 4 and 6.
• Current vertex 4 do same process again as in the above mark it as visited and add to the path[] now it contains four elements 0, 1, 3, and 4 check it is destination vertex no then go to adjacency list of current vertex 4 which contains 5.check vertex 5 is visited not go to the vertex 5 and recall the function again to find the path between 5 and 6.
  
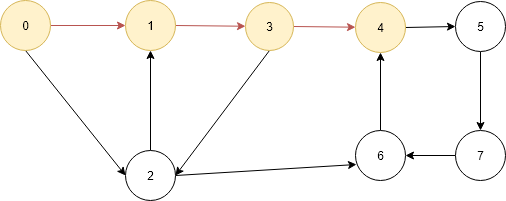
• Current vertex is 5 do same mark it as visited and add to the path[] now it contains 0, 1, 3, 4 and 5.check if current vertex 5 is destination vertex no then go to adjacency list of vertex 5 which contains 7. Check vertex 7 is visited no then go to vertex 7 and recall the function to find the path between 7 and 6.
  
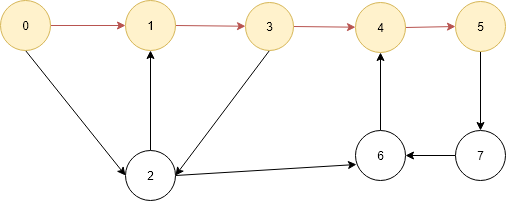
• Current vertex is 7 mark it as visited and add to the path[] now it contains 0, 1, 3, 4, 5 and 7.check if current vertex 7 is destination vertex no then go to adjacency list of vertex 7 which contains 6. Check vertex 6 is visited no then go to vertex 6 and recall the function to find the path between 6 and 6.
  
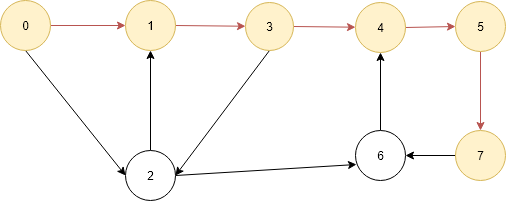
• Current vertex is 6 mark it as visited and add to the path[] now it contains 0, 1, 3, 4, 5, 7 and 6.check if current vertex 6 is destination vertex yes then print the path and mark vertex 6 as not visited and delete it from path once again as explain above.
  
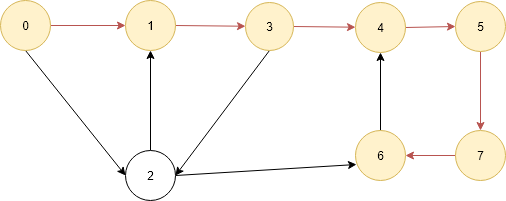
• Do same thing again go get the last two paths as mention above.
• So we need visit every node many times to get all the paths.

Complexity Analysis:

Time Complexity: O((2^V)(V+E))

We can have exponentially many paths, and for each such path, our prepending operation will be O(V+E). If we want check the path between two node exist or not then it can be checked in in one DFS O(V+E).

Space Complexity: O((2^V) * V), the size of the output dominating the final space complexity.