
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 12 minutes
By the property of Binary search tree we know that by doing Indorder Traversal of Binary search tree gives us the sorted elements.
The Idea is do the inorder traversal of binary tree and store it in an array.Then find the minimum number of swaps require to sort an array which is the output we want.
How to do Indorder Traversal of Binary Tree?
Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways.one of the way is Inorder Traversal.
Algorithm Inorder(tree)
1. Traverse the left subtree, i.e., call Inorder(left-subtree)
2. Visit the root.
3. Traverse the right subtree, i.e., call Inorder(right-subtree)
Implementation of the above algorithm.
// C++ program for Indorder Traversal tree traversals
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout << node->data << " ";
/* now recur on right child */
printInorder(node->right);
}
/* Driver program to test above functions*/
int main()
{
struct Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "Inorder traversal of binary tree is \n";
printInorder(root);
return 0;
}
Output:
Inorder traversal of binary tree is
4 2 5 1 3
Explanation:
- First go to the left most node of the tree therefore recur util the left child of a node becomes null.
- Then print the the data of the current node.
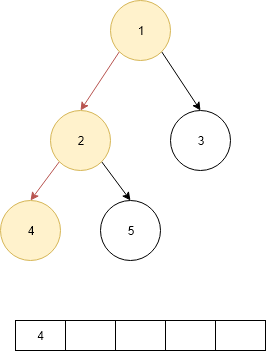
- Then check the right child if it is null go to parent node.
- Now print the data of current node.
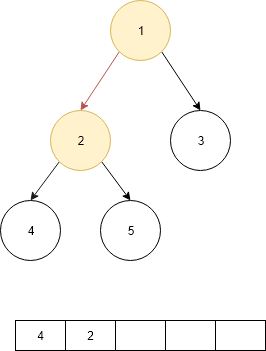
- Now check the right child if it is no null go to that node.
- print that data of current node.
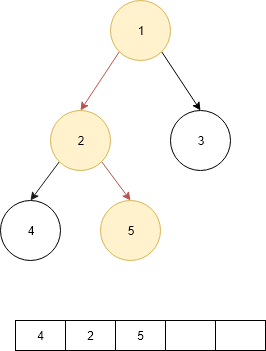
- Now check if the right child is null then go to the parent until the node is not null.
- When Node is not equal to null print the data of the node.
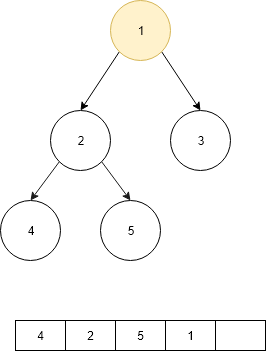
- Then go the right child of the node and if the node is not equal to null the print the data of the node.
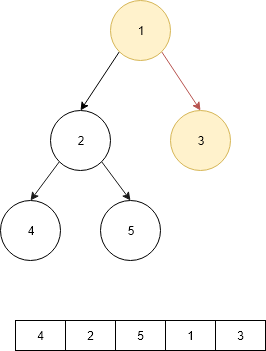
How to find the Minimum Number of Swaps to form the sorted array?
Given an array of n distinct elements, find the minimum number of swaps required to sort the array.
Examples:
Input: {4,2,5,1,3}
Ouput: 2
Explanation : Swap index 0 with 3 and 2 with 4 to
form the sorted array {1, 2, 3, 4, 5}.
This can be easily done by visualizing the problem as a graph. We will have n nodes and an edge directed from node i to node j if the element at i’th index must be present at j’th index in the sorted array.
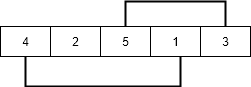
The graph will now contain many non-intersecting cycles. Now a cycle with 2 nodes will only require 1 swap to reach the correct ordering.
Hence,
summation of i 1 to k.
- ans = Σ i =(cycle_size – 1)
where k is the number of cycles
Below is the implementation of the idea.
Approach:
- Create an array of pairs where first element is array element and second element is position of first element.
- Sort the array by array element values to get right position of every element as second element of pair.
- To keep track of visited elements. Initialize all elements as not visited or false.
- Traverse array elements and find out the number of node in this cycle and add in ans and Update answer by adding current cycle.
Implementation of above approach.
// C++ program to find minimum number of swaps
// required to sort an array
#include<bits/stdc++.h>
using namespace std;
// Function returns the minimum number of swaps
// required to sort the array
int minSwaps(int arr[], int n)
{
// Create an array of pairs where first
// element is array element and second element
// is position of first element
pair<int, int> arrPos[n];
for (int i = 0; i < n; i++)
{
arrPos[i].first = arr[i];
arrPos[i].second = i;
}
// Sort the array by array element values to
// get right position of every element as second
// element of pair.
sort(arrPos, arrPos + n);
// To keep track of visited elements. Initialize
// all elements as not visited or false.
vector<bool> vis(n, false);
// Initialize result
int ans = 0;
// Traverse array elements
for (int i = 0; i < n; i++)
{
// already swapped and corrected or
// already present at correct pos
if (vis[i] || arrPos[i].second == i)
continue;
// find out the number of node in
// this cycle and add in ans
int cycle_size = 0;
int j = i;
while (!vis[j])
{
vis[j] = true;
j = arrPos[j].second;
cycle_size++;
}
// Update answer by adding current cycle.
if (cycle_size > 0)
{
ans += (cycle_size - 1);
}
}
return ans;
}
// Driver program to test the above function
int main()
{
int arr[] = {4, 2, 5, 1, 3};
int n = (sizeof(arr) / sizeof(int));
cout << minSwaps(arr, n);
return 0;
}
Output:
2
Now by combing above two methods we will get the minimum number of swaps to convert the binary tree into binary search tree
Approach:
- Do the Inoder Traversal of the binary tree and store the elements of tree in an array.
- Then find the minimum number of swaps require to make the array sorted which is made from above process and store it in result and give as output.
Implementation of the above approach.
// C++ program for Indorder Traversal tree traversals
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
vector<int> arr;
/* Given a binary tree, print its nodes in inorder*/
void InorderTraversal(struct Node* node)
{
if (node == NULL)
return;
/* first recur on left child */
InorderTraversal(node->left);
/* store the data of node in array */
arr.push_back(node->data);
/* now recur on right child */
InorderTraversal(node->right);
}
// Function returns the minimum number of swaps
// required to sort the array
int minSwaps(struct Node* node)
{
InorderTraversal(node);
int n = arr.size();
// Create an array of pairs where first
// element is array element and second element
// is position of first element
pair<int, int> arrPos[n];
for (int i = 0; i < n; i++)
{
arrPos[i].first = arr[i];
arrPos[i].second = i;
}
// Sort the array by array element values to
// get right position of every element as second
// element of pair.
sort(arrPos, arrPos + n);
// To keep track of visited elements. Initialize
// all elements as not visited or false.
vector<bool> vis(n, false);
// Initialize result
int ans = 0;
// Traverse array elements
for (int i = 0; i < n; i++)
{
// already swapped and corrected or
// already present at correct pos
if (vis[i] || arrPos[i].second == i)
continue;
// find out the number of node in
// this cycle and add in ans
int cycle_size = 0;
int j = i;
while (!vis[j])
{
vis[j] = true;
j = arrPos[j].second;
cycle_size++;
}
// Update answer by adding current cycle.
if (cycle_size > 0)
{
ans += (cycle_size - 1);
}
}
return ans;
}
/* Driver program to test above functions*/
int main()
{
struct Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
cout << "Minimum number of swaps required: "<<minSwaps(root);
return 0;
}
Output:
Minimum number of swaps required: 2
Explanation of this code can be also seen from above explained two methods.
