Sum of k smallest elements in Binary Search Tree

Reading time: 30 minutes | Coding time: 10 minutes

Given a binary search tree and a integer k our task is to find out sum of all the elements which is less or equal to the k th smallest element in binary search tree.
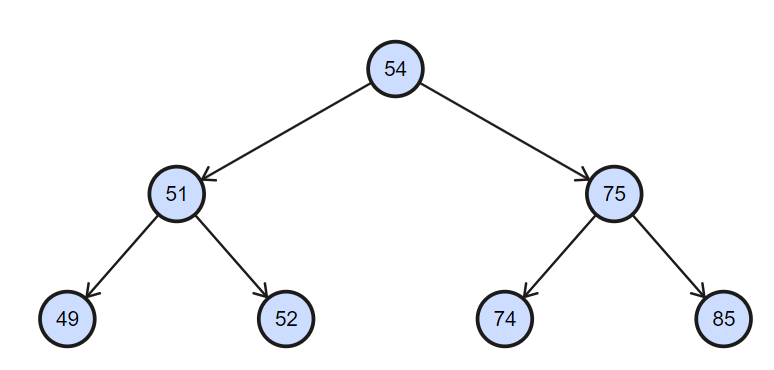
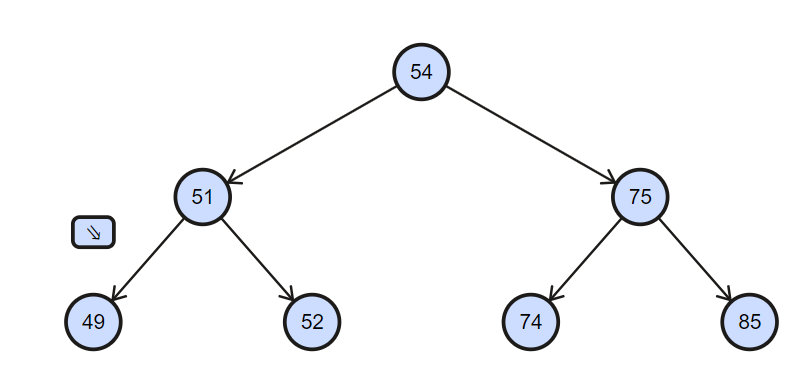
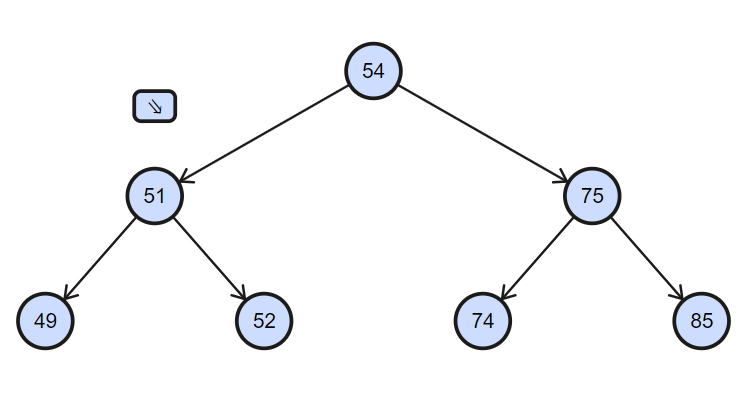
For example for given below binary search tree and k=3.

Explanation: so here in above example k th smallest element is 52 and sum of all the elements which is less or equal to 52 is 152.

We will explore two approaches:

• Naive approach O(N)
• Efficient approach O(log N)

Naive Approach

This is a simple approach this takes O(n) time and O(1) extra space.

Algorithm:

1. Do inorder traversal of binary search tree and and count the visited elements and add all the elements to a variable.
2. when count is equal to k return the variable having sum of all the elements until that point and that is the output.

Implementation of above algorithm is given below.

// c++ program to find Sum Of All Elements smaller 
// than or equal to Kth Smallest Element In BST 
#include <bits/stdc++.h> 
using namespace std; 

/* Binary tree Node */
struct Node 
{ 
	int data; 
	Node* left, * right; 
}; 

// utility function new Node of BST 
struct Node *createNode(int data) 
{ 
	Node * new_Node = new Node; 
	new_Node->left = NULL; 
	new_Node->right = NULL; 
	new_Node->data = data; 
	return new_Node; 
} 

// A utility function to insert a new Node 
// with given key in BST and also maintain lcount ,Sum 
struct Node * insert(Node *root, int key) 
{ 
	// If the tree is empty, return a new Node 
	if (root == NULL) 
		return createNode(key); 

	// Otherwise, recur down the tree 
	if (root->data > key) 
		root->left = insert(root->left, key); 

	else if (root->data < key) 
		root->right = insert(root->right, key); 

	// return the (unchanged) Node pointer 
	return root; 
} 

// function return sum of all element smaller than 
// and equal to Kth smallest element 
int ksmallestElementSumRec(Node *root, int k, int &count) 
{ 
	// Base cases 
	if (root == NULL) 
		return 0; 
	if (count > k) 
		return 0; 

	// Compute sum of elements in left subtree 
	int res = ksmallestElementSumRec(root->left, k, count); 
	if (count >= k) 
		return res; 

	// Add root's data 
	res += root->data; 

	// Add current Node 
	count++; 
	if (count == k) 
	return res; 

	// If count is less than k, return right subtree Nodes 
	return res + ksmallestElementSumRec(root->right, k, count); 
} 

// Wrapper over ksmallestElementSumRec() 
int ksmallestElementSum(struct Node *root, int k) 
{ 
int count = 0; 
ksmallestElementSumRec(root, k, count); 
} 

/* Driver program to test above functions */
int main() 
{ 

	
	Node *root = NULL; 
	root = insert(root, 54); 
	root = insert(root, 51); 
	root = insert(root, 49); 
	root = insert(root, 52); 
	root = insert(root, 75); 
	root = insert(root, 74); 
	root = insert(root, 85); 

	int k = 3; 
    cout <<"Sum of k smallest elements is " << ksmallestElementSum(root, k) <<endl; 
	return 0; 
} 

Output:

Sum of k smallest element is 152

Explanation:

• First of all go to the left most element and add to the a variable is out case it is res and increment the counter by 1. so now res = 49 and count = 1. Now check if count is equal to three no then go the another element.
  
• Now current node is 51 add it to the res and increase counter by 1 now res = 100 and count = 2 check if count if equal to k no then go to the another element.
  
• Now current node is 52 add it to the res and increase counter by 1 now res = 152 and count = 3 check if count if equal to k yes then return res and it is required output.
  

Efficient Approach

Here we use augmented tree data structure to solve this problem efficiently in O(h) time [ h is height of Binary Search Tree ] .

Structure of Augmented Tree

Binary Search Tree Node contain to extra fields : lCount , Sum

For each Node of Binary Search Tree
lCount : store how many left child it has
Sum : store sum of all left child it has

Insertion In Augmented Tree

1. When we insert a node in this tree if key value is less then current node value then add key value to the sum of the current node and increment lcount by 1 of that node. if key value is greater than current node then go to the right similar to binary tree.
2. Do above process to all he nodes which come in the way till you don't reach the insertion point.
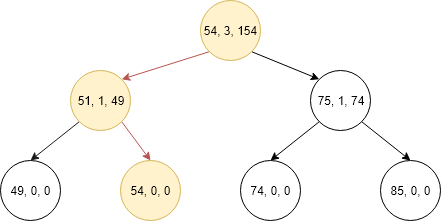
   For example binary search tree given below we want insert 49 in it.
   
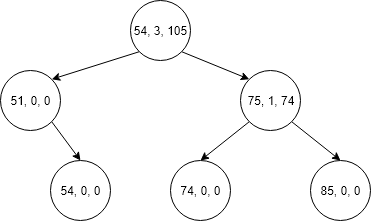
   Now tree becomes as shown below.
   

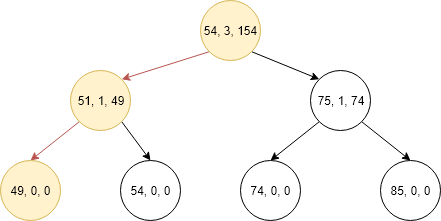
Algorithm for finding sum of k smallest elements in Binary Search Tree

Find Kth smallest element
[ temp_sum store sum of all element less than equal to K ]

ksmallestElementSumRec(root, K, temp_sum)

  IF root -> lCount == K + 1
      temp_sum += root->data + root->sum;
      break;
  ELSE
     IF k > root->lCount   // Goto right sub-tree
        temp_sum += root->data + root-> sum;
        ksmallestElementSumRec(root->right, K-root->lcount+1, temp_sum)
     ELSE
        // Goto left sun-tree
        ksmallestElementSumRec( root->left, K, temp_sum)

Implementation of above algorithm is given below.

// C++ program to find Sum Of All Elements smaller 
// than or equal t Kth Smallest Element In BST 
#include <bits/stdc++.h> 
using namespace std; 

/* Binary tree Node */
struct Node 
{ 
	int data; 
	int lCount; 
	int Sum ; 
	Node* left; 
	Node* right; 
}; 

//utility function new Node of BST 
struct Node *createNode(int data) 
{ 
	Node * new_Node = new Node; 
	new_Node->left = NULL; 
	new_Node->right = NULL; 
	new_Node->data = data; 
	new_Node->lCount = 0 ; 
	new_Node->Sum = 0; 
	return new_Node; 
} 

// A utility function to insert a new Node with 
// given key in BST and also maintain lcount ,Sum 
struct Node * insert(Node *root, int key) 
{ 
	// If the tree is empty, return a new Node 
	if (root == NULL) 
		return createNode(key); 

	// Otherwise, recur down the tree 
	if (root->data > key) 
	{ 
		// increment lCount of current Node 
		root->lCount++; 

		// increment current Node sum by adding 
		// key into it 
		root->Sum += key; 

		root->left= insert(root->left , key); 
	} 
	else if (root->data < key ) 
		root->right= insert (root->right , key ); 

	// return the (unchanged) Node pointer 
	return root; 
} 

// function return sum of all element smaller than and equal 
// to Kth smallest element 
void ksmallestElementSumRec(Node *root, int k , int &temp_sum) 
{ 
	if (root == NULL) 
		return ; 

	// if we fount k smallest element then break the function 
	if ((root->lCount + 1) == k) 
	{ 
		temp_sum += root->data + root->Sum ; 
		return ; 
	} 

	else if (k > root->lCount) 
	{ 
		// store sum of all element smaller than current root ; 
		temp_sum += root->data + root->Sum; 

		// decremented k and call right sub-tree 
		k = k -( root->lCount + 1); 
		ksmallestElementSumRec(root->right , k , temp_sum); 
	} 
	else // call left sub-tree 
		ksmallestElementSumRec(root->left , k , temp_sum ); 
} 

// Wrapper over ksmallestElementSumRec() 
int ksmallestElementSum(struct Node *root, int k) 
{ 
	int sum = 0; 
	ksmallestElementSumRec(root, k, sum); 
	return sum; 
} 

/* Driver program to test above functions */
int main() 
{ 
    Node *root = NULL; 
	root = insert(root, 20); 
	root = insert(root, 8); 
	root = insert(root, 4); 
	root = insert(root, 12); 
	root = insert(root, 10); 
	root = insert(root, 14); 
	root = insert(root, 22); 

	int k = 3; 
    cout<<"Sum of k smallest is " << ksmallestElementSum(root, k) << endl; 
	return 0; 
} 

Output:

Sum of k smallest element is 152

Explanation:

• First of all go to the root and compare k with lcount + 1 if it is equal then temp_sum = 208 and return otherwise if k<lCount then go the left child of the root.
  
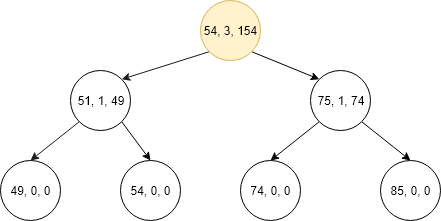
• Now compare the lCount + 1 of current node with k if it is equal then temp_sum = 100 and return if k>lCount the go to right and temp_sum = 100 and k = 1.
  
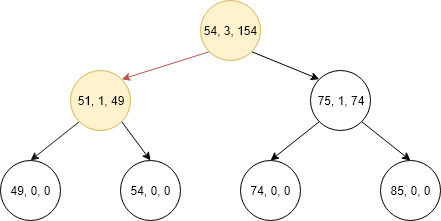
• Now again compare lCount + 1 with k if it is equal then temp_sum = 152 and return.