
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
This article is about the analysis of time and space complexity of queue operations. With this, we will also learn what the time and space complexity are and how we can calculate the time and space complexity of an algorithm.
In this article, we have covered the following:
- Some standard queue operations.
- Implementation of Queue using LinkedList
- Implementation of Queue using Array
- What is algorithm analysis?
- Analyzing the time and space complexity of those implementations (or operations).
- Conclusion
Pre-requisites:
Following is the summary for a quick review:
Time and space complexity using array:
| Operation | Best | Average | Worst | Best | Average | Worst |
|---|---|---|---|---|---|---|
| isEmpty() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| enqueue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| dequeue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| count() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| peek() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| show() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
Time and space complexity using LinkedList:
| Operation | Best | Average | Worst | Best | Average | Worst |
|---|---|---|---|---|---|---|
| isEmpty() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| enqueue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| dequeue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| count() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| peek() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| show() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
Queue Operations:
-
isEmpty(): Check if queue is empty or not.
-
enqueue(): Elements are added form one end (rear/back).
-
dequeue(): Elements are removed from one end.
-
peek() : Get the value of the front of the queue without removing it.
-
count() : Gets count of total items in queue.
-
show() : To show the content of the queue.
Implementation of Queue using LinkedList
#include <stdio.h>
#include <stdlib.h>
struct queue{
int num;
struct queue *next;
};
struct queue *front= NULL;
struct queue *rear= NULL;
int main(){
enqueue(10);
enqueue(20);
printf("Dequeue : %d\n", dequeue());
printf("Dequeue : %d\n", dequeue());
enqueue(30);
enqueue(40);
enqueue(50);
printf("Peek : %d\n", peek());
printf("Size of the queue is : %d\n",count());
show();
return 0;
}
Output
Dequeue : 10
Dequeue : 20
Peek : 30
Size of the queue is : 3
30 40 50
Implementation of Queue using Array
According to the concept of the queue, It follows the FIFO rule. Insertion is from the rear end, and deletion is from the front end. But in the case of the linear queue when the array is full,Then even if we delete some elements, they remain in the array as garbage elements. We can't store any further data in our queue.
when queue is full, rear= queue(size) -1
To overcome this problem, we use a circular queue or we implement the Queue using the circular array.
A circular Array is nothing but a simple array; only the pointer (front/rear) will be reset to its start position when it reaches the end. Treating the array as a circular buffer, pointing the head of the Queue to the next item when one is removed becomes as simple as a single assignment, which is much more performant.
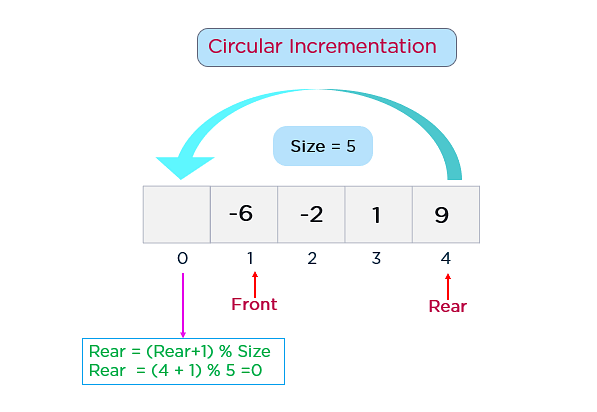
Queue is full, when (rear+1)%size==front
#include <stdio.h>
int queue[8];
int front=-1;
int rear=-1;
int size=8;
int main() {
// Write C code here
enqueue(10);
enqueue(20);
printf("Dequeue : %d\n", dequeue());
printf("Dequeue : %d\n", dequeue());
enqueue(30);
enqueue(40);
enqueue(50);
printf("Peek : %d\n", peek());
printf("Size of the queue is : %d\n",count());
show();
return 0;
}
Output
Dequeue : 10
Dequeue : 20
Peek : 30
Size of the queue is : 3
30 40 50
Let us practice Algorithm analysis by analyzing the complexity of queue operation.
What is Algorithm analysis?
Algorithm analysis is a study to provide theoretical estimation for the required resources of an algorithm to solve a specific computational problem.
Generally, there are multiple approaches or methods, or algorithms to solve one problem statement.
Algorithm analysis is performed to figure out which is the better or optimum approach or algorithm out of the options.
What does a better algorithm mean?
- Faster (Less execution time) - Time complexity
- Less memory - Space complexity
- Easy to read
- Less line of code.
Generally, the efficiency of an algorithm is related to the input length (number of steps), known as time complexity, or volume of memory known as space complexity.
Some facts:
There is a little bit of misconception when it comes to calculating
space complexity.
For any algorithm, memory is required for the following purposes-
I. To store program instructions
II. To store constant values.
III. To store the variable values.
IV. For function calls, jumping statements, etc.
Space complexity is calculated in terms of auxiliary space and
space used by input. But, most of the time, the amount of space
used by the Input is ignored. Because when we say space complexity,
we focus on how much extra space our algorithm needs.
Auxiliary space:
It is the temporary space (excluding the input size) allocated
by your algorithm to solve the problem concerning input size.
Complexity Analysis of Queue Operations
If we break our code into a few fragments, it will be easier to understand.Some instructions are in the whole function that once being executed. So they will take constant time to be complete.
isEmpty() Operation

Time complexity calculation
By looking at these two algorithms, it is clear that each instruction takes constant time to execute. So, its time complexity will always be constant for best, average and worst cases.
Time Complexity : O(1)
Space complexity calculation
Auxiliary space
These two algorithms don't use any auxiliary space.
Space Complexity = K1(constant)
Space Complexity : O(1)
Enqueue operation:

Time complexity calculation
Case 1: Using Array
Here we have broken the code into two fragments (F1, F2).
So looking at the fragments, we understand that the time complexity of each fragment is constant here.
Let us assume,
the execution time for the F1 fragment is K1, F2 fragment is K2.
Where all the K1 and K2 are constant.
In a function call only one fragment is executed.
Total time is taken by the algorithm to complete its work-
Tn= K
So here we see that time complexity does not depend on the input value.
In terms of Big -O notation, the time complexity of this algorithm is O(1).
Case 2: Using LinkedList
The time complexity of each fragments is constant.
Let us assume,
the execution time for the f1 fragment is k1, f2 fragment is k2, f3 is k3.
Where all the k1, k2, k3 are constant.
In a function call only one fragment is executed.
So here we see that time complexity does not depend on the input value.
In terms of Big -O notation, the time complexity of this algorithm is O(1).
So, let's try to find the time complexities in different cases.
Best case:
-
When your queue is empty and you are going to add the first element inside the queue.
-
let us assume, our queue is not empty and you can still put elements in your queue. And you only have one element left to put on. In that case, you will need the enqueue() operation only once to keep that one element.
Suppose we have 7 elements as
7, 6, 8, 9, 11, 5, 23
Out of which we have already inserted some elements in the queue.

So we just have to add 23 to the queue.
In that case Time complexity = O(1)
Worst case:
Array Implementation:
Worst case condition will start when our queue is full. With the help of Circular Array, we have already solved the problem of garbage elements. So now we can dequeue some elements as we need and can put a new element in its place.
Suppose, our queue is full, and it contains N elements.
We have to insert another N element in our queue.
What can we do then?
We have to remove all the N elements from our queue. Then we need to insert the new N elements inside the queue.
One dequeue() operation takes O(1) time.
To remove N elements from the queue will take O(N) time (in total).
Similarly, One enqueue () operation takes O(1) time.
To insert N elements in the queue will take O(N) time (in total).
Then, T(N) = O(N) + O(N) = 2* O(N)
Time complexity = O(N) ( Drop the constant term).
LinkedList Implementation:
The concept will remain the same. Only here we do not have to remove any elements from the queue.
We have to insert another N element in our queue.
One enqueue () operation takes O(1) time.
To insert N elements in the queue will take O(N) time.
Time complexity = O(N) ( Drop the constant term).
Average Case:

Suppose we have n number of elements for our queue. Then maybe we have to insert one element, maybe two or more than two, or we need to insert n elements. Maybe our queue is full, or may not.There is also a possibility that we need not have to add any elements.
Let us assume, each enqueue operation takes k time to complete.
So, total number of possibilities,
(i) n+1 (In case of linked list)
(ii) n+n+1= 2*n+1 (In case of array)
Because in this case, two conditions can occur.
When queue is not full, we can add elements to the queue.
When queue is full, then also we can add a new element by performing a dequeue operation.
Let us assume, One enqueue() operation takes K time to complete and one dequeue() operation takes K1 time to complete.
LinkedList Implementation:

Array Implementation:
We have made the calculations. Here you have to understand all the possibilities.
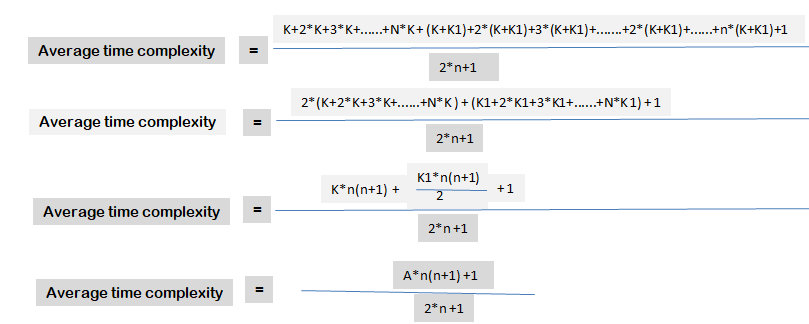
For large value of n,
n+1≈ n and 2*n +1 ≈ 2*n

Average time complexity : O(n) (Drop the constant term)
Space complexity calculation
Case 1: Using Array
Auxiliary space
This algorithm does not use any auxiliary space.
Space Complexity = K1(constant) for best, average, and worst case.
In terms of Big -O notation, the space complexity of this algorithm is O(1).
Case 2: Using LinkedList
Auxiliary space
We have only created another node type variable in the function,no dynamic space is being allocated here.
Space Complexity = K1(constant)
In terms of Big -O notation, the space complexity of this algorithm is O(1).
When the function finally exits, its local storage is deallocated. So, for each enqueue operation, the algorithm will take a constant amount of storage.
The best, average,and worst case complexity is O(1).
Dequeue Operation
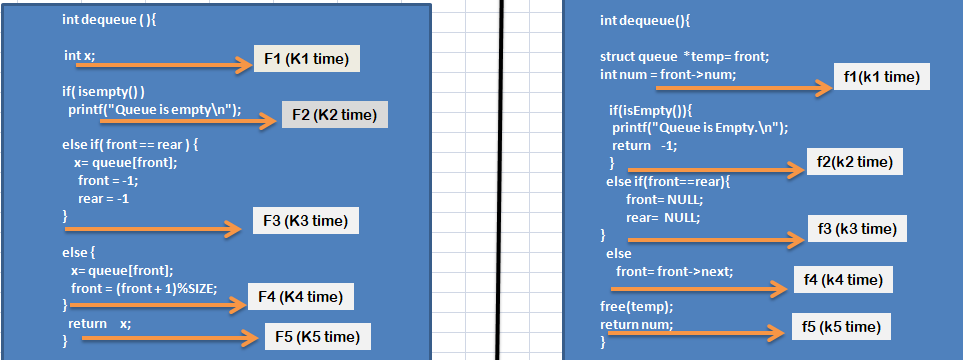
Time complexity calculation
Case 1: Using Array
The execution time for the F1 fragment is K1, F2 fragment is K2, F3 is K3 and F4 is K4 and F5 is K5.
Where all the K1, K2, K3, K4 are constant.
In a function call only one fragment is executed(except F1 and F5).
Total time is taken by the algorithm to complete its work-
Tn= K
In terms of Big -O notation, the time complexity of this algorithm is O(1).
Case 2: Using LinkedList
The time complexity of each fragments is constant.
Execution time for the f1 fragment is k1, f2 fragment is k2, f3 is k3, and f4 is k4 and f5 is k5.
Where all the k1, k2, k3,k4 and k5 are constant.
In a function call only one fragment is executed(except f1 and f5).
In terms of Big -O notation, the time complexity of this algorithm is O(1).
Let's try to find the time complexities in different cases.
Best case:
When the queue is empty, or the queue contains only one element.
To remove that one element from the queue, the algorithm will take constant time.
Time complexity: O(1)
Worst case:
When the queue is full, and we have to remove all elements from that queue one by one.
Let us assume, each dequeue operation takes K times, and our queue size is n.
So, time complexity will be K*n
Time complexity(in terms of big-O): O(n)
Average case:
Suppose we have n number of elements in our queue. Then maybe we have to remove one element, maybe two or more than two, or we need to remove all the n elements. There is also a possibility that we need not have to remove any elements.
Let us assume, each dequeue operation takes k time to complete.

Space complexity calculation
Case 1: Using Array
Auxiliary space
One variable x to store the current front value.No dynamic space is being allocated here.
Space Complexity = K1(constant)
In terms of Big -O notation, the space complexity of this algorithm is O(1).
Case 2: Using LinkedList
Auxiliary space
- A queue type node.
- A variable to store the front of the queue.
No dynamic space is being allocated here.
Space complexity = constant
In terms of Big -O notation, the space complexity of this algorithm is O(1).
These two algorithms have used this auxiliary space.
When the function finally exits, its local storage is deallocated. So, for each enqueue operation, the algorithm will take a constant amount of storage.
The best, average,and worst case complexity is O(1).
Count Operation

Time complexity calculation
Case 1: Using Array
Fragment F1, F2, and F3 will take constant time to execute. Again, F2, F3, and (F4, F5) are not be executed together. But F4 and F5 will execute together.
But, the Complexity of the Algorithm is determined by considering the worst-case scenario.
For F4 and F5, Consider the Image given below.
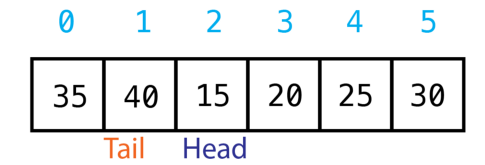
Consider the Tail as rear and consider the Head as the front.
We can see that the elements are arranged in two groups.
i) From front to last index position.
ii) From first index position to rear.
Let us think for the sake of calculation, we have 2n elements.
In the first group, we have n elements. The rest of the n elements are present in the second group.
So from here, we can easily say that the loops present in both F4 and F5 fragments will run n times.
Then, K4= k4*n and K5= k5*n
( k4 and k5 is the time taken to execute the operation inside the loop.)
Total time= K1+K2+K3+K4+K5 = K1+K2+K3+(k4+k5)n = A+ Bn
Time complexity = O(n) (Drop the non-dominant and constant term).
(Please note that Here we describe the worst-case scenario of the
count operation.)
Case 2: Using LinkedList
Fragment F1 and Fragment F2 will take constant time to execute. Again, F2 and F3 are not be executed together.
But, the Complexity of the Algorithm is determined by considering the worst-case scenario.
For F3,
Let us assume,
res++; temp= temp->next; these two instructions take K time to be executed.
and also let us consider the queue size is n.
We can easily say that,This loop will run n times.
while(temp!=NULL)
{
res++;
temp=temp->next;
}
So, K3= K*n
Total time, Tn= K1 +K2+ K3 = K4+K*n
when n>> K4
Tn= K*n= O(n)
Time Complexity: O(n)
Best case:
Array:
- When the queue is empty.
- When
front<=rear
Time complexity: O(1)
LinkedList
When the queue is empty or queue containing only one element(In that case loop will run only once.).
Time complexity: O(1)
Worst case:
Array:
When, front>rear and the front and rear are located side by side.
See the calculation.
Time complexity : O(n)
LinkedList:
When the queue is full and the queue size is very large.
Let us assume queue size is n.(n is very large)
then , T(n)= k3= k*n
T(n)= O(n)
Time complexity : O(n)
Average case:
Array:
Time complexity: O(n) (Usually, The F4 and F5 fragments will execute in the average case).
LinkedList:
Then maybe we have one element, maybe two or more than two, or we need to count n elements. There is also a possibility that queue is empty.
Then the time complexity = time taken by fragment f2 +time taken by fragment f3
time complexity = k2+ k*n
Time complexity= O(n).
Space complexity calculation
Case 1: Using Array
Auxiliary space
1.One counter variable (i)
2.One integer variable to store the result.
Space Complexity = K1(constant) (For the three cases)
Space Complexity : O(1)
When the function finally exits, its local storage is deallocated.
Case 2: Using LinkedList
Auxiliary space
- A queue type node.
- A variable to store the result.
No dynamic space is being allocated here.When the function finally exits, its local storage is deallocated.
Space complexity = constant
Space Complexity: O(1)
Peek Operation

Time complexity calculation
By looking at these two algorithms, it is clear that each instruction takes constant time to execute.
Time Complexity : O(1) (For the three cases)
Space complexity calculation
Auxiliary space
These two algorithms don't use any auxiliary space.
Space Complexity = K1(constant)
Space Complexity : O(1)
Display Operation

Time complexity calculation
Case 1: Using Array
Fragment F1 takes K1 times to execute. Similarly, F2 takes K2, F3 takes K3, F4 takes K4 and F5 takes K5 times to execute.
Fragments F2, F3,(F4 and F5) are not executed together.
Let us find out the execution times of all the fragments to find out the total time complexity.
F1 and F2 will take constant time to execute.
For F3,
Let us think at that moment queue contains n elements.
So there are n elements present in the Queue from front to the rear.
Suppose, The execution times of the operation and instruction present inside the loop is K.
The loop will run n times.
So, K3= K*n
For F4 and F5,
K4= k4*n
K5= k5*n
See the calculation here.
Total time, Tn= K1 + K2 + K3 + K4 + K5 = K1 + K2 + Kn + k4n + k5n = A + Bn
Tn= O(n) (Drop the non-dominant and constant term.)
Time Complexity: O(n)
Case 1: Using LinkedList
Fragment f1 and Fragment f2 will take constant time to execute. Again, f2 and f3 are not be executed together.
For f3,
Suppose there are currently n elements in the queue.
Then, this loop will run n times.
while(temp!=NULL){
printf("%d ",temp->num);
temp= temp->next;
}
Let us assume,
printf("%d ",temp->num);temp= temp->next; these two instructions take K time to be executed.
So, k3= K*n+1
Total time, Tn= k1 +k2+k3 = k4+K*n
when n>> k4
Tn= K*n= O(n)
Time Complexity: O(n)
Best case:
Array:
- When the queue is empty.
- When
front<=rearand queue contains only one elements.
Time complexity: O(1) (The loop will run only once.)
LinkedList:
When queue is empty or queue contains only one element.
Time complexity: O(1) (The loop will run only once.)
Worst case:
Array:
When the array size is very large,
front<= reararray is full with the elements.
for(int i= front; i<=rear; i++)
printf("%d ",queue[i]);
This loop will run n times (where, n is the number of elements)
Time complexity: O(n)
- When,
front>rearand the front and rear are located side by side.
See the calculation.
Time complexity : O(n)
LinkedList:
When the queue is full and the queue size is very large.
Let us assume queue size is n.(n is very large)
then , T(n)= k3= k*n
T(n)= O(n)
Time complexity : O(n)
Average case:
Array:
Time complexity: O(n) (Usually, The F3,F4 and F5 fragments will execute in the average case.).
LinkedList:
Then maybe we have one element, maybe two or more than two, or we need to print n elements. There is also a possibility that queue is empty.
Then the time complexity = time taken by fragment f2 +time taken by fragment f3
time complexity = k2+ k*n
Time complexity= O(n).
Space complexity calculation
Case 1: Using Array
Auxiliary space
One counter variable.
Space Complexity: O(1) (For best, average and worst cases.)
Case 2: Using LinkedList
Auxiliary space
One temporary queue-type node.
Space Complexity: O(1) (For best, average and worst cases.)
These are some basic operations of Queue data structure.
Conclusion
Algorithm analysis does not give you accurate or exact values. However, it gives estimates which can be used to study the behavior of the algorithm.
Time and space complexity using array:
| Operation | Best | Average | Worst | Best | Average | Worst |
|---|---|---|---|---|---|---|
| isEmpty() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| enqueue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| dequeue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| count() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| peek() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| show() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
Time and space complexity using LinkedList:
| Operation | Best | Average | Worst | Best | Average | Worst |
|---|---|---|---|---|---|---|
| isEmpty() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| enqueue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| dequeue() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| count() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
| peek() | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| show() | O(1) | O(N) | O(N) | O(1) | O(1) | O(1) |
With this article at OpenGenus, you must have the complete idea of Time and Space Complexity of Queue operations.
