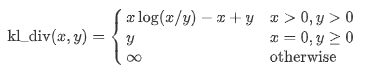Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 15 minutes
Topic Modeling falls under unsupervised machine learning where the documents are processed to obtain the relative topics. It is a very important concept of the traditional Natural Processing Approach because of its potential to obtain semantic relationship between words in the document clusters. In addition that, it has numerous other applications in NLP.
Some of the well known approaches to perform topic modeling are
- Non-Negative Matrix Factorization (NMF)
- Latent Dirichlet Allocation (LDA)
- Latent Semantic Analysis (LSA)
I have explained the other methods in my other articles. Now let us have a look at the Non-Negative Matrix Factorization.
Non-Negative Matrix Factorization
Non-Negative Matrix Factorization is a statistical method to reduce the dimension of the input corpora. It uses factor analysis method to provide comparatively less weightage to the words with less coherence.
For a general case, consider we have an input matrix V of shape m x n. This method factorizes V into two matrices W and H, such that the dimension of W is m x k and that of H is n x k. For our situation, V represent the term document matrix, each row of matrix H is a word embedding and each column of the matrix W represent the weightage of each word get in each sentences ( semantic relation of words with each sentence). You can find a practical application with example below.
But the assumption here is that all the entries of W and H is positive given that all the entries of V is positive.
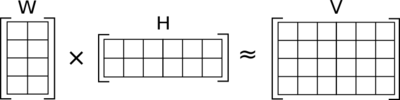
Now let us look at the mechanism in our case. Suppose we have a dataset consisting of reviews of superhero movies. In the document term matrix (input matrix), we have individual documents along the rows of the matrix and each unique term along the columns. In case, the review consists of texts like Tony Stark, Ironman, Mark 42 among others. It may be grouped under the topic Ironman. In this method, each of the individual words in the document term matrix are taken into account. While factorizing, each of the words are given a weightage based on the semantic relationship between the words. But the one with highest weight is considered as the topic for a set of words. So this process is a weighted sum of different words present in the documents.
Math behind NMF
As mentioned earlier, NMF is a kind of unsupervised machine learning. The main core of unsupervised learning is the quantification of distance between the elements. The distance can be measured by various methods. Some of them are Generalized Kullback–Leibler divergence, frobenius norm etc.
1. Generalized Kullback–Leibler divergence
It is a statistical measure which is used to quantify how one distribution is different from another. Closer the value of Kullback–Leibler divergence to zero, the closeness of the corresponding words increases. In other words, the divergence value is less.
Let us look at the difficult way of measuring Kullback–Leibler divergence. Formula for calculating the divergence is given by.
Python Implementation of the formula is shown below.
from numpy import sum
def kullback_leibler_divergence(p, q):
return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))
a=[0.78, 0.25, 0.98, 0.35]
b=[0.58, 0.46, 0.28, 0.17]
kullback_leibler_divergence(a, b)
There is also a simple method to calculate this using scipy package.
from scipy.special import kl_div
a=[0.78, 0.25, 0.98, 0.35]
b=[0.58, 0.46, 0.28, 0.17]
print(kl_div(a,b))
2. Frobenius Norm
The other method of performing NMF is by using Frobenius norm. It is defined by the square root of sum of absolute squares of its elements. It is also known as eucledian norm. The formula and its python implementation is given below.
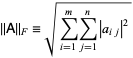
import numpy as np
a=[0.78, 0.25, 0.98, 0.35]
frobenius_norm = numpy.linalg.norm(a)
An optimization process is mandatory to improve the model and achieve high accuracy in finding relation between the topics. There are two types of optimization algorithms present along with scikit-learn package.
- Coordinate Descent Solver
- Multiplicative update Solver
NMF in action
Why should we hard code everything from scratch, when there is an easy way? Packages are updated daily for many proven algorithms and concepts. We have a scikit-learn package to do NMF. We will use the 20 News Group dataset from scikit-learn datasets. We will first import all the required packages.
# Importing Necessary packages
import numpy as np
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import NMF
Now let us import the data and take a look at the first three news articles.
# Importing Data
text_data= fetch_20newsgroups(remove=('headers', 'footers', 'quotes')).data
text_data[:3]
Output of the snippet is shown below.
['I was wondering if anyone out there could enlighten me on this car I saw\nthe other day. It was a 2-door sports car, looked to be from the late 60s/\nearly 70s. It was called a Bricklin. The doors were really small. In addition,\nthe front bumper was separate from the rest of the body. This is \nall I know. If anyone can tellme a model name, engine specs, years\nof production, where this car is made, history, or whatever info you\nhave on this funky looking car, please e-mail.',
"A fair number of brave souls who upgraded their SI clock oscillator have\nshared their experiences for this poll. Please send a brief message detailing\nyour experiences with the procedure. Top speed attained, CPU rated speed,\nadd on cards and adapters, heat sinks, hour of usage per day, floppy disk\nfunctionality with 800 and 1.4 m floppies are especially requested.\n\nI will be summarizing in the next two days, so please add to the network\nknowledge base if you have done the clock upgrade and haven't answered this\npoll. Thanks.",
'well folks, my mac plus finally gave up the ghost this weekend after\nstarting life as a 512k way back in 1985. sooo, i'm in the market for a\nnew machine a bit sooner than i intended to be...\n\ni'm looking into picking up a powerbook 160 or maybe 180 and have a bunch\nof questions that (hopefully) somebody can answer:\n\n* does anybody know any dirt on when the next round of powerbook\nintroductions are expected? i'd heard the 185c was supposed to make an\nappearence "this summer" but haven't heard anymore on it - and since i\ndon't have access to macleak, i was wondering if anybody out there had\nmore info...\n\n* has anybody heard rumors about price drops to the powerbook line like the\nones the duo's just went through recently?\n\n* what's the impression of the display on the 180? i could probably swing\na 180 if i got the 80Mb disk rather than the 120, but i don't really have\na feel for how much "better" the display is (yea, it looks great in the\nstore, but is that all "wow" or is it really that good?). could i solicit\nsome opinions of people who use the 160 and 180 day-to-day on if its worth\ntaking the disk size and money hit to get the active display? (i realize\nthis is a real subjective question, but i've only played around with the\nmachines in a computer store breifly and figured the opinions of somebody\nwho actually uses the machine daily might prove helpful).\n\n* how well does hellcats perform? ;)\n\nthanks a bunch in advance for any info - if you could email, i'll post a\nsummary (news reading time is at a premium with finals just around the\ncorner... :( )\n--\nTom Willis \ twillis@ecn.purdue.edu \ Purdue Electrical Engineering']
Now, we will convert the document into a term-document matrix which is a collection of all the words in the given document.
# converting the given text term-document matrix
vectorizer = TfidfVectorizer(max_features=1500, min_df=10, stop_words='english')
X = vectorizer.fit_transform(text_data)
words = np.array(vectorizer.get_feature_names())
print(X)
print("X = ", words)
Output of the snippet is given below.
(0, 1472) 0.18550765645757622
(0, 278) 0.6305581416061171
(0, 1191) 0.17201525862610717
(0, 411) 0.1424921558904033
(0, 469) 0.20099797303395192
(0, 808) 0.183033665833931
(0, 767) 0.18711856186440218
(0, 484) 0.1714763727922697
(0, 273) 0.14279390121865665
(0, 1118) 0.12154002727766958
(0, 1256) 0.15350324219124503
(0, 128) 0.190572546028195
(0, 1218) 0.19781957502373115
(0, 1158) 0.16511514318854434
(0, 247) 0.17513150125349705
(0, 757) 0.09424560560725694
(0, 887) 0.176487811904008
(0, 506) 0.1941399556509409
(0, 1495) 0.1274990882101728
(0, 672) 0.169271507288906
(0, 707) 0.16068505607893965
(0, 809) 0.1439640091285723
(0, 829) 0.1359651513113477
(1, 411) 0.14622796373696134
(1, 546) 0.20534935893537723
: :
(11312, 1486) 0.183845539553728
(11312, 1409) 0.2006451645457405
(11312, 926) 0.2458009890045144
(11312, 1100) 0.1839292570975713
(11312, 1276) 0.39611960235510485
(11312, 1302) 0.2391477981479836
(11312, 647) 0.21811161764585577
(11312, 1027) 0.45507155319966874
(11312, 1482) 0.20312993164016085
(11312, 554) 0.17342348749746125
(11312, 1146) 0.23023119359417377
(11312, 534) 0.24057688665286514
(11313, 506) 0.2732544408814576
(11313, 950) 0.38841024980735567
(11313, 801) 0.18133646100428719
(11313, 18) 0.20991004117190362
(11313, 666) 0.18286797664790702
(11313, 637) 0.22561030228734125
(11313, 46) 0.4263227148758932
(11313, 1394) 0.238785899543691
(11313, 272) 0.2725556981757495
(11313, 1225) 0.30171113023356894
(11313, 1219) 0.26985268594168194
(11313, 1457) 0.24327295967949422
(11313, 244) 0.27766069716692826
X = ['00' '000' '01' ... 'york' 'young' 'zip']
Defining term document matrix is out of the scope of this article. In brief, the algorithm splits each term in the document and assigns weightage to each words.
Now, let us apply NMF to our data and view the topics generated. For ease of understanding, we will look at 10 topics that the model has generated. We will use Multiplicative Update solver for optimizing the model. It is available from 0.19 version.
# Applying Non-Negative Matrix Factorization
nmf = NMF(n_components=10, solver="mu")
W = nmf.fit_transform(X)
H = nmf.components_
for i, topic in enumerate(H):
print("Topic {}: {}".format(i + 1, ",".join([str(x) for x in words[topic.argsort()[-10:]]])))
Now the topics are listed below.
Topic 1: really,people,ve,time,good,know,think,like,just,don
Topic 2: info,help,looking,card,hi,know,advance,mail,does,thanks
Topic 3: church,does,christians,christian,faith,believe,christ,bible,jesus,god
Topic 4: league,win,hockey,play,players,season,year,games,team,game
Topic 5: bus,floppy,card,controller,ide,hard,drives,disk,scsi,drive
Topic 6: 20,price,condition,shipping,offer,space,10,sale,new,00
Topic 7: problem,running,using,use,program,files,window,dos,file,windows
Topic 8: law,use,algorithm,escrow,government,keys,clipper,encryption,chip,key
Topic 9: state,war,turkish,armenians,government,armenian,jews,israeli,israel,people
Topic 10: email,internet,pub,article,ftp,com,university,cs,soon,edu
For crystal clear and intuitive understanding, look at the topic 3 or 4. In topic 4, all the words such as "league", "win", "hockey" etc. are related to sports and are listed under one topic.
The Factorized matrices thus obtained is shown below.
W matrix can be printed as shown below. For the sake of this article, let us explore only a part of the matrix.
print(W[:10,:10])
[[3.14912746e-02 2.94542038e-02 0.00000000e+00 3.33333245e-03
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[6.20557576e-03 2.95497861e-02 1.07989433e-08 5.19817369e-04
3.18118742e-02 8.04393768e-03 0.00000000e+00 4.99785893e-03
2.82899920e-08 2.95957405e-04]
[6.57082024e-02 6.11330960e-02 0.00000000e+00 8.18622592e-03
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[3.51420347e-03 2.70163687e-02 0.00000000e+00 0.00000000e+00
0.00000000e+00 2.25431949e-02 0.00000000e+00 8.78948967e-02
0.00000000e+00 4.75400023e-17]
[3.43312512e-02 6.34924081e-04 3.12610965e-03 0.00000000e+00
0.00000000e+00 2.41521383e-02 1.04304968e-02 0.00000000e+00
0.00000000e+00 1.10050280e-02]
[1.54660994e-02 0.00000000e+00 3.72488017e-03 0.00000000e+00
2.73645855e-10 3.59298123e-03 8.25479272e-03 0.00000000e+00
1.79357458e-02 3.97412464e-03]
[7.64105742e-03 6.41034640e-02 3.08040695e-04 2.52852526e-03
0.00000000e+00 5.67481009e-03 0.00000000e+00 0.00000000e+00
2.12149007e-02 4.17234324e-03]
[3.82228411e-06 4.61324341e-03 7.97294716e-04 4.09126211e-16
1.14143186e-01 8.85463161e-14 0.00000000e+00 2.46322282e-02
3.40868134e-10 9.93388291e-03]
[6.82290844e-03 3.30921856e-02 3.72126238e-13 0.00000000e+00
0.00000000e+00 0.00000000e+00 2.34432917e-02 6.82657581e-03
0.00000000e+00 8.26367144e-26]
[1.66278665e-02 1.49004923e-02 8.12493228e-04 0.00000000e+00
2.19571524e-02 0.00000000e+00 3.76332208e-02 0.00000000e+00
1.05384042e-13 2.72822173e-09]]
H matrix is given below.
print(H[:10,:10])
[[1.81147375e-17 1.26182249e-02 2.93518811e-05 1.08240436e-02
6.18732299e-07 1.27435805e-05 9.91130274e-09 1.12246344e-05
4.51400032e-69 3.01041384e-54]
[2.21534787e-12 0.00000000e+00 1.33321050e-09 2.96731084e-12
2.65374551e-03 3.91087884e-04 2.98944644e-04 6.24554050e-10
9.53864192e-31 2.71257642e-38]
[0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00]
[6.31863318e-11 4.40713132e-02 1.77561863e-03 2.19458585e-03
2.15120339e-03 2.61656616e-06 2.14906622e-03 2.30356588e-04
3.83769479e-08 1.28390795e-07]
[3.98775665e-13 4.07296556e-03 0.00000000e+00 9.13681465e-03
0.00000000e+00 0.00000000e+00 4.33946044e-03 0.00000000e+00
1.28457487e-09 2.25454495e-11]
[1.00421506e+00 2.39129457e-01 8.01133515e-02 5.32229171e-02
3.68883911e-02 7.27891875e-02 4.50046335e-02 4.26041069e-02
4.65075342e-03 2.51480151e-03]
[0.00000000e+00 0.00000000e+00 2.17982651e-02 0.00000000e+00
1.39930214e-02 2.16749467e-03 5.63322037e-03 5.80672290e-03
2.53163039e-09 1.44639785e-12]
[0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 5.91572323e-48]
[4.57542154e-25 1.70222212e-01 3.93768012e-13 7.92462721e-03
6.35542835e-18 0.00000000e+00 9.92275634e-20 4.14373758e-10
3.70248624e-47 7.69329108e-42]
[0.00000000e+00 0.00000000e+00 0.00000000e+00 1.18348660e-02
1.90271384e-02 0.00000000e+00 7.34412936e-03 0.00000000e+00
0.00000000e+00 0.00000000e+00]]
It is quite easy to understand that all the entries of both the matrices are only positive.
Don't trust me? Go on and try hands on yourself. By following this article, you can have an in-depth knowledge of the working of NMF and also its practical implementation. If you have any doubts, post it in the comments.
When can we use this approach?
- NMF by default produces sparse representations. This mean that most of the entries are close to zero and only very few parameters have significant values. This can be used when we strictly require fewer topics.
- NMF produces more coherent topics compared to LDA.
Source:
- https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html
- https://towardsdatascience.com/kl-divergence-python-example-b87069e4b810
Image Courtesy: