
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Introduction:
AO* algorithm is a best first search algorithm. AO* algorithm uses the concept of AND-OR graphs to decompose any complex problem given into smaller set of problems which are further solved. AND-OR graphs are specialized graphs that are used in problems that can be broken down into sub problems where AND side of the graph represent a set of task that need to be done to achieve the main goal , whereas the or side of the graph represent the different ways of performing task to achieve the same main goal.
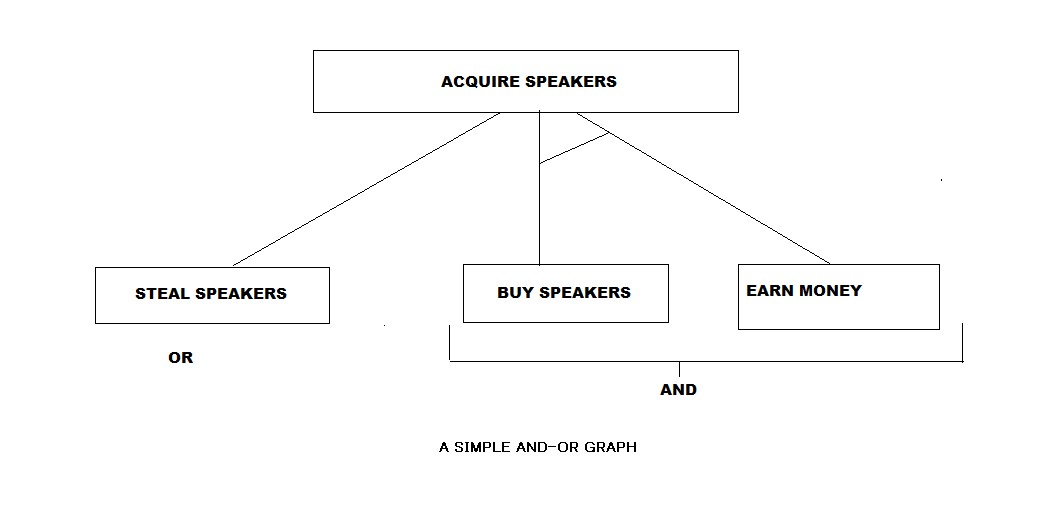
In the abovc figure we can see an example of a simple AND-OR graph wherein, the acquisition of speakers can be broken into sub problems/tasks that could be performed to finish the main goal. The sub task is to either steal speakers which will directly helps us achieve the main goal "or" earn some money "and" buy speakers which helps us achieve the main goal. The AND part of the graphs are represented by the AND-ARCS, referring that all the sub problems with the AND-ARCS need to be solved for the predecessor node or problem to be completed. The edges without AND-ARCS are OR sub problems that can be done instead of the sub problems with And-arcs. It is to be noted that several edges can come from a single node as well as the presence of multiple AND arcs and multiple OR sub problems are possible.
The AO* algorithm is a knowledge-based search technique, meaning the start state and the goal state is already defined , and the best path is found using heuristics. The time complexity of the algorithm is significantly reduced due to the informed search technique.Compared to the A* algorithm , AO* algorithm is very efficient in searching the AND-OR trees very efficiently.
Working of AO algorithm:
The AO* algorithm works on the formula given below :
f(n) = g(n) + h(n)
where,
- g(n): The actual cost of traversal from initial state to the current state.
- h(n): The estimated cost of traversal from the current state to the goal state.
- f(n): The actual cost of traversal from the initial state to the goal state.
Now, to get a better idea of the AO* algorithm lets take a look at an example.
Example-
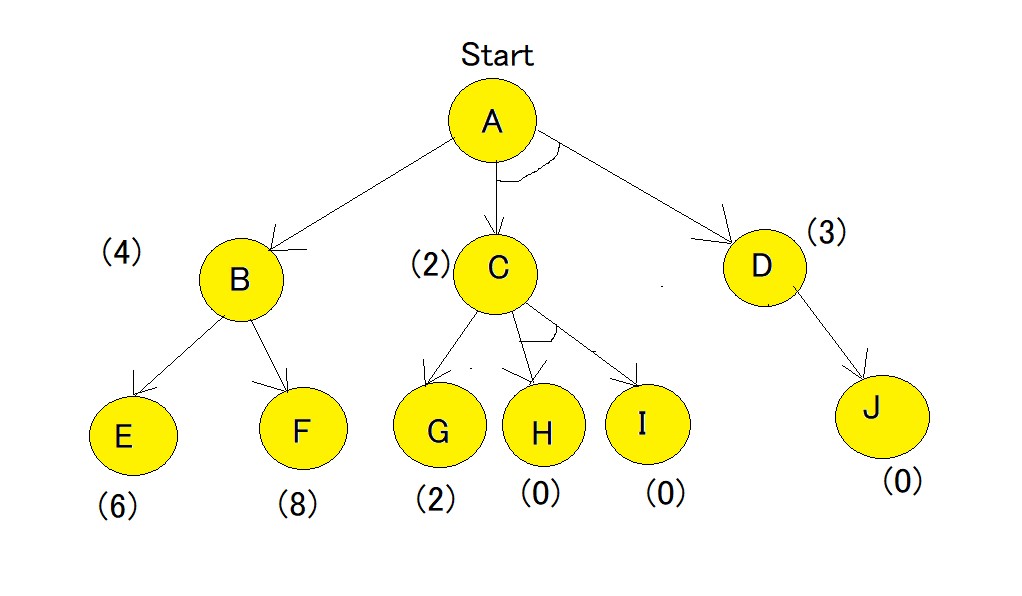
Here, in the above example all numbers in brackets are the heuristic value i.e h(n). Each edge is considered to have a value of 1 by default.
Step-1
Starting from node A, we first calculate the best path.
f(A-B) = g(B) + h(B) = 1+4= 5 , where 1 is the default cost value of travelling from A to B and 4 is the estimated cost from B to Goal state.
f(A-C-D) = g(C) + h(C) + g(D) + h(D) = 1+2+1+3 = 7 , here we are calculating the path cost as both C and D because they have the AND-Arc. The default cost value of travelling from A-C is 1, and from A-D is 1, but the heuristic value given for C and D are 2 and 3 respectively hence making the cost as 7.
The minimum cost path is chosen i.e A-B.
Step-2
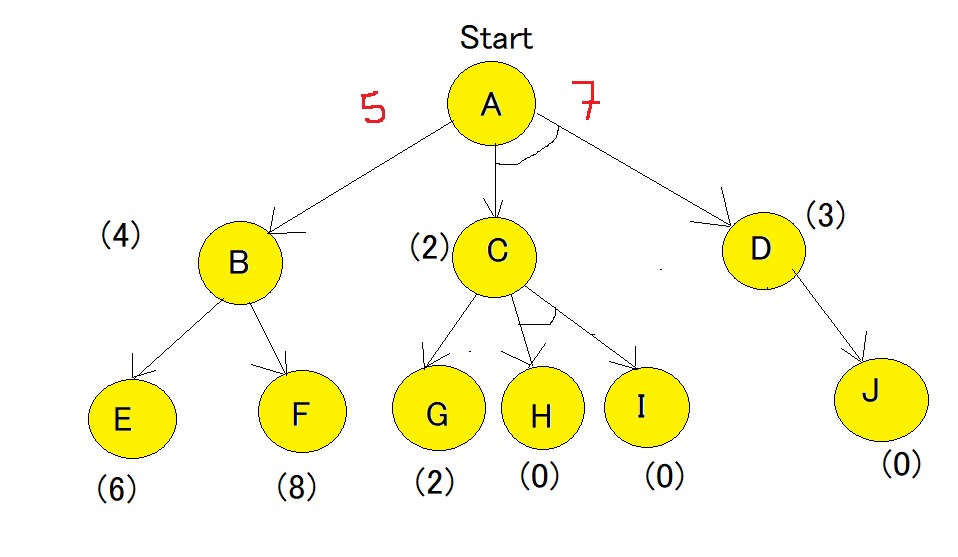
Using the same formula as step-1, the path is now calculated from the B node,
f(B-E) = 1 + 6 = 7.
f(B-F) = 1 + 8 = 9
Hence, the B-E path has lesser cost. Now the heuristics have to be updated since there is a difference between actual and heuristic value of B. The minimum cost path is chosen and is updated as the heuristic , in our case the value is 7. And because of change in heuristic of B there is also change in heuristic of A which is to be calculated again.
f(A-B) = g(B) + updated((h(B)) = 1+7=8
Step-3
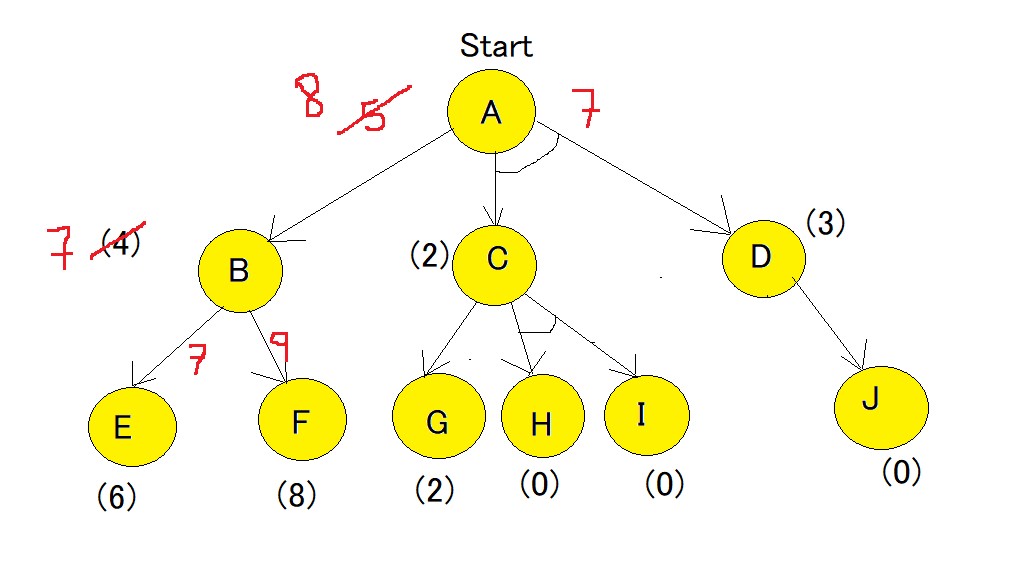
Comparing path of f(A-B) and f(A-C-D) it is seen that f(A-C-D) is smaller. Hence f(A-C-D) needs to be explored.
Now the current node becomes C node and the cost of the path is calculated,
f(C-G) = 1+2 = 3
f(C-H-I) = 1+0+1+0 = 2
f(C-H-I) is chosen as minimum cost path,also there is no change in heuristic since it matches the actual cost. Heuristic of path of H and I are 0 and hence they are solved, but Path A-D also needs to be calculated , since it has an AND-arc.
f(D-J) = 1+0 = 1, hence heuristic of D needs to be updated to 1. And finally the f(A-C-D) needs to be updated.
f(A-C-D) = g(C) + h(C) + g(D) + updated((h(D)) = 1+2+1+1 =5.
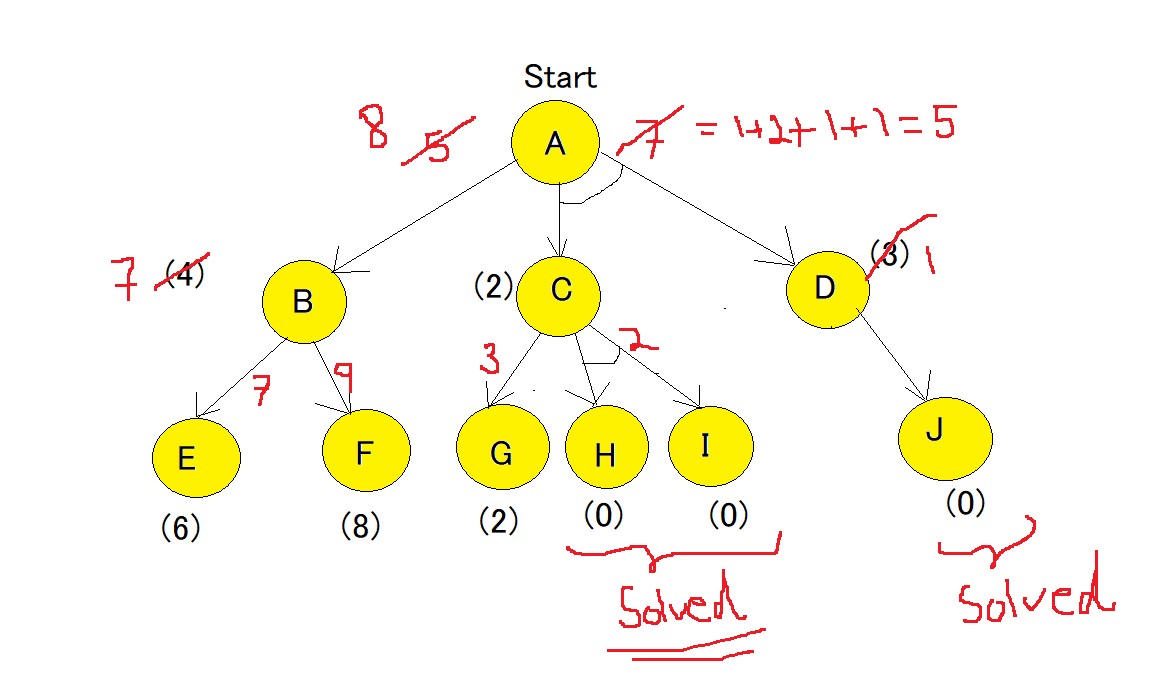
As we can see that the solved path is f(A-C-D).
What is the difference between A* Algorithm and AO* algorithm?
- A* algorithm provides with the optimal solution, whereas AO* stops when it finds any solution.
- AO* algorithm requires lesser memory compared to A* algorithm.
- AO* algorithm doesn't go into infinite loop whereas the A* algorithm can go into an infinite loop.
FAQ's:
Q: What is an informed search?
- Any search where the goal state as well as the path to reach the goal is defined is known as informed search. Generally makes use of heuristics to make the path defined.
Q: What makes the AND-OR graph efficient?
- If the cost function of first branch of AND-graph is more than the calculated cost of OR graph , the Algorithm directly picks the path of the OR graph and continues to traverse, this method is also known as short circuiting.
