Reading time: 30 minutes

Centroid Decomposition is a divide and conquer technique which is used on trees.
The centroid decomposition of a tree is another tree defined recursively as:

• Its root is the centroid of the original tree.
• Its children are the centroid of each tree resulting from the removal of the root(centroid) from the original tree.

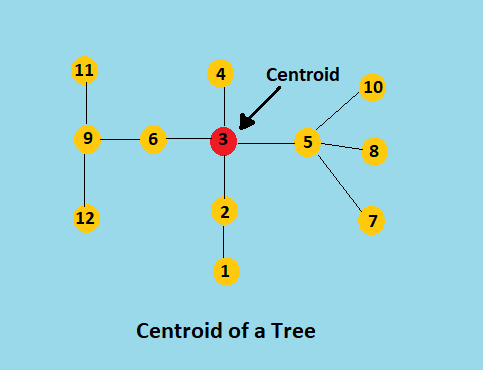
Centroid of a Tree
Given a tree with N nodes, a centroid is a node whose removal splits the given tree into a forest of trees, where each of the resulting tree contains no more than N/2 nodes.

Algorithm

Finding the centroid of a tree
One way to find the centroid is to pick an arbitrary root, then run a depth-first search computing the size of each subtree, and then move starting from root to the largest subtree until we reach a vertex where no subtree has size greater than N/2. This vertex would be the centroid of the tree i.e. Centroid is a node v such that,

maximum(N - S(v), S(u1, S(u2, .. S(um) <= N/2
where ui is ith child of v,
and S(u) is the size(number of nodes in tree) of subtree rooted at u.

Algorithm

1. Select arbitrary node v
2. Start a DFS from v, and setup subtree sizes
3. Re-position to node v (or start at any arbitrary v that belongs to the tree)
4. Check mathematical condition of centroid for v
   1. If condition passed, return current node as centroid
   2. Else move to adjacent node with greatest subtree size, and back to step 4.

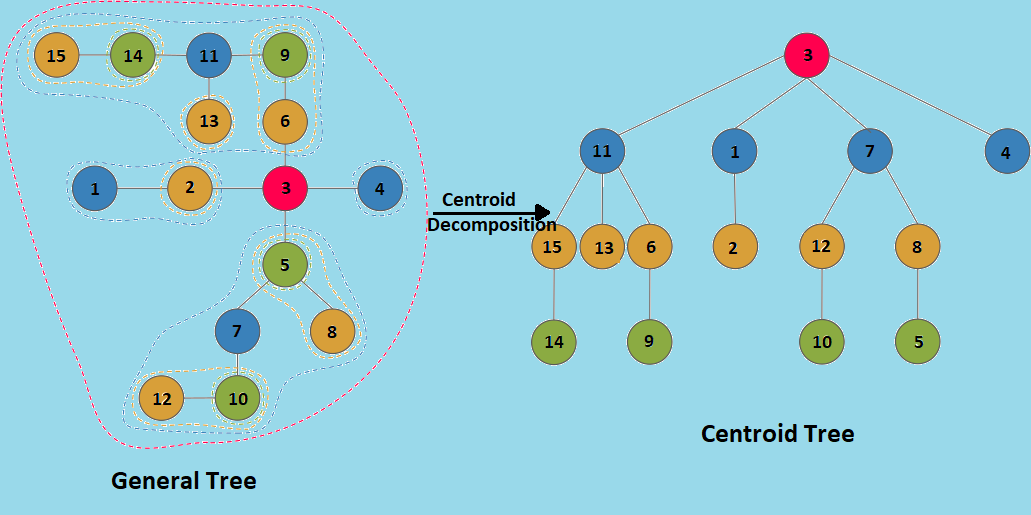
Decomposing the Tree to get the new "Centroid Tree"
On removing the centroid, the original given tree decomposes into a number of different trees, each having no of nodes < N/2 . We make this centroid the root of our centroid tree and then recursively decompose each of the new trees formed and attach their centroids as children to our root. Thus , a new centroid tree is formed from the original tree.

Algorithm

1. Make the centroid as the root of a new tree (which is centroid tree).
2. Recursively decompose the trees in the resulting forest.
3. Make the centroids of these trees as children of the centroid which last split them.

example: For the following tree:

Number of children of any node of a tree can be O(logN) in the worst case. So in each find_centroid operation which takes O(N) time in worst case, we divide the tree into forest of O(logN) subtrees, so we recur at most O(logN) times. So overall centroid decomposition of a tree takes O(N logN) time in the worst case.

Implementation

Code in Python3

import sys

class Tree:
    def __init__(self, n):
        self.size = n + 1
        self.cur_size = 0
        self.tree = [[] for _ in range(self.size)]
        self.iscentroid = [False] * self.size
        self.ctree = [[] for _ in range(self.size)]
    
    def dfs(self, src, visited, subtree):
        visited[src] = True
        subtree[src] = 1
        self.cur_size += 1
        for adj in self.tree[src]:
            if not visited[adj] and not self.iscentroid[adj]:
                self.dfs(adj, visited, subtree)
                subtree[src] += subtree[adj]
    
    def findCentroid(self, src, visited, subtree):
        iscentroid = True
        visited[src] = True
        heavy_node = 0
        for adj in self.tree[src]:
            if not visited[adj] and not self.iscentroid[adj]:
                if subtree[adj] >  self.cur_size//2:
                    iscentroid = False
                
                if heavy_node == 0 or subtree[adj] > subtree[heavy_node]:
                    heavy_node = adj
            
        if iscentroid and self.cur_size - subtree[src] <= self.cur_size//2:
            return src
        else:
            return self.findCentroid(heavy_node, visited, subtree)

    def findCentroidUtil(self, src):
        visited = [False] * self.size
        subtree = [0] * self.size
        self.cur_size = 0
        self.dfs(src, visited, subtree)
        for i in range(self.size):
            visited[i] = False
        centroid = self.findCentroid(src, visited, subtree)
        self.iscentroid[centroid] = True
        return centroid

    def decomposeTree(self, root):
        centroid_tree = self.findCentroidUtil(root)
        print(centroid_tree, end=' ')
        for adj in self.tree[centroid_tree]:
            if not self.iscentroid[adj]:
                centroid_subtree = self.decomposeTree(adj)
                self.ctree[centroid_tree].append(centroid_subtree)
                self.ctree[centroid_subtree].append(centroid_tree)
            
        return centroid_tree

    def addEdge(self, src, dest):
        self.tree[src].append(dest)
        self.tree[dest].append(src)
    

if __name__ == '__main__':
    tree = Tree(15)
    # A tree with 15 nodes
    tree.addEdge(1, 2)
    tree.addEdge(2, 3)
    tree.addEdge(3, 4)
    tree.addEdge(3, 5)
    tree.addEdge(3, 6)
    tree.addEdge(5, 7)
    tree.addEdge(5, 8)
    tree.addEdge(6, 9)
    tree.addEdge(7, 10)
    tree.addEdge(9, 11)
    tree.addEdge(10, 12)
    tree.addEdge(11, 13)
    tree.addEdge(11, 14)
    tree.addEdge(14, 15)

    print("DFS traversal of generated Centroid tree is:")
    tree.decomposeTree(1)

Output

DFS traversal of generated Centroid tree is:
3 2 1 4 7 5 8 10 12 11 9 6 13 14 15

Complexity

Time Complexity

• DFS of tree takes O(N) time.
• Find_Centroid of tree takes O(N) time.
• Centroid Decomposition of tree takes overall O(N logN) time.

Space Complexity

• DFS of tree takes O(N) space.
• Adjacency list of tree takes O(N²) auxiliary space in worst case.
• Overall time space used by Centroid Decomposition algorithm is O(N²)

Application

Centroid Decomposition of tree is a vastly used divide and conquer technique in competitive programming. Here is a list of problems where we use centroid decomposition to solve the problem:

• Xenia and Tree
• BST maintenance
• Prime Distance on Tree

References

• Centroid Decomposition article on cs.ubc.ca.
• Centroid Decomposition page on mit.edu
• Centroid Decomposition blog page on Codeforces