
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 10 minutes
In this article, we have explored the <complex.h> header file in C. The header file complex.h defines macros and functions to carry out operations on complex numbers in C.
#include <complex.h>
The general syntax for any complex number is c=x+iy .
Depending on type of x and y there are three data types in C for complex numbers:
- double complex
- float complex
- long double complex
Example of initialisation of a complex variable:
double complex z1 = 1.0 + 3.0 * I;
double complex z2 = 1.0 - 4.0 * I;
‘I’ is used instead of ‘i’ for the imaginary unit due to the the widespread use of i as counter in loops.
The application can use a different identifier, say j, for the imaginary unit by following the inclusion of the <complex.h> header with:
#undef I
#define j _Imaginary_I
Finally, while compiling the file, do
gcc <file_name> -lm.
Now we shall look at some of the most useful functions in complex.h
Functions and Examples
1. creal :
Returns the real part value of the complex number
Function definitions:
double creal(double complex z);
float crealf(float complex z);
long double creall(long double complex z);
printf("real part of Z1 = %.2f \n", creal(z1));
Output:
real part of Z1 = 1.00
All the following functions can be used for all the three datatypes by adding an ‘f’ to the function name for floating complex numbers and ‘l’ to the function name for long double complex numbers. Since its repetitive the function definition handling double complex numbers are given from hereon.
2. cimag :
Returns the imaginary part value of the complex number
Function definition:
double cimag(double complex z);
printf("Imaginary part of Z1 = %.2f \n", cimag(z1));
Output:
Imaginary part of Z1 = 3.00
For a variable z of type complex:
z == creal(z) + cimag(z)*I
3. conj :
Returns the complex conjugate value
Function definition:
double conj(double complex z);
double complex conjugate = conj(z1);
printf("The conjugate of Z1 = %.2f %+.2fi\n", creal(conjugate), cimag(conjugate));
Output:
The conjugate of Z1 = 1.00 -3.00i
4. cabs:
Returns the complex absolute value (also called norm, modulus, or magnitude) of z
Function definition:
double cabs(double complex z);
double abs = cabs(z1);
printf("The absolute value of Z1 = %.2f \n",abs);
Output:
The absolute value of Z1 = 3.16
5.cpow:
Computes the complex power function x^y, with a branch cut for the first parameter along the negative real axis
Function definition:
double complex cpow(double complex x, double complex y);
double complex power=cpow(z1,z2);
printf("Z1 raised to power Z2 = %.2f %+.2fi\n", creal(power), cimag(power));
Output:
Z1 raised to power Z2 = -456.82 +99.53i
6.cexp:
Computes the complex exponent of z, defined as e^z.
Function definition:
double complex cexp(double complex z);
double complex exp=cexp(z1);
printf("The exp of Z1 = %.2f %+.2fi\n", creal(exp), cimag(exp));
Output:
The exp of Z1 = -2.69 +0.38i
7.clog:
Computes the complex natural (base e) logarithm of z, with a branch cut along the negative real axis.The range is mathematically unbounded along the real axis and in the interval [-i, +i] along the imaginary axis.
Function Definition:
double complex clog(double complex z);
double complex log=clog(z1);
printf("The log of Z1 = %.2f %+.2fi\n", creal(log), cimag(log));
Output:
The log of Z1 = 1.15 +1.25i
8.csqrt:
Computes the complex square root of z, with a branch cut along the negative real axis.The range of the function is the right half-plane (including the imaginary axis).
Function definition:
double complex csqrt(double complex z);
double complex sqrt=csqrt(z1);
printf("The sqrt of Z1 = %.2f %+.2fi\n", creal(sqrt), cimag(sqrt));
Output:
The sqrt of Z1 = 1.44 +1.04i
9.csin:
Computes the complex sine of z
Function definition:
double complex csin(double complex z)
double complex sinP=csin(z1);
printf("The sin of Z1 = %.2f %+.2fi\n", creal(sinP), cimag(sinP));
Output:
The sin of Z1 = 8.47 +5.41i
10. casin:
Returns the complex arc sine value, in the range of a strip mathematically unbounded along the imaginary axis and in the interval [-pi/2, +pi/2] along the real axis.
Function definition:
double complex casin(double complex z);
double complex z4=8.47 +5.41*I;//sin of z1
z3=casin(z4);
printf("The sine inverse of Z4 = %.2f %+.2fi\n", creal(z3), cimag(z3));
Output:
The sine inverse of Z4 = 1.00 +3.00i
- Similarly cxos,cacos, ctan, catan functions can be used.
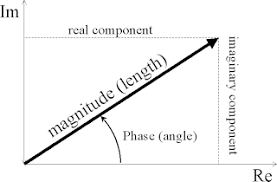
11.carg:
Computes the argument (also called phase angle) of z, with a branch cut along the negative real axis.These functions shall return the value of the argument in the interval [-pi, +pi].
- The phase angle is in radians and not degrees.
Function definition:
double carg(double complex z);
double complex z3=1.0 + 0.0*I;
double phase=carg(z3);
printf("The phase of Z3 = %.2f\n",phase);
Output:
The phase of Z3 = 0.00
Applications
Complex analysis comes up in a lot of areas related to enginering. Being able to perform operations on complex numbers is essential while solving differential and quadratic equations.
Systems such as damped oscillaors and solving fourier transforms and series all require complex analysis.
Programs emulating such systems, if written in C, will require the use of the <
Question
The real part of a complex number z is given by -
With this article at OpenGenus, you must have a complete idea of using complex numbers in C using the complex header file.
