In this article at OpenGenus, we have explained merge sort and implemented a program on the same in C Programming Language.

Table of contents

• What is merge sort?
• How merge sort works
• Approach to write the program
• Implementation
• Output
• Time complexity
• Benefits of merge sort

What is Merge sort?

Merge sort is a sorting algorithm that works by dividing the main array into smaller arrays and sorting each of the smaller arrays and putting them back together.

How Merge sort works

• For example if we have the given array
  
• First we divide the given array in two equal halves.
  
• Now we again divide of the peach portion of the array.
• By dividing this subarray we have 3 single element arrays, so we sort it and all single element arrays are sorted so we now sort the right portion of the subarray(that is the blue portion)
  
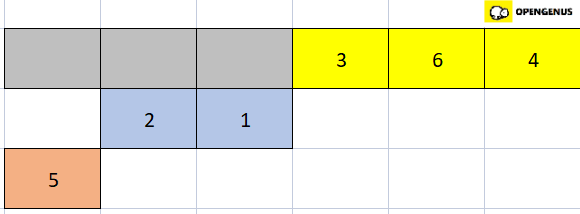
• Now the right portion of the subarray is sorted
  
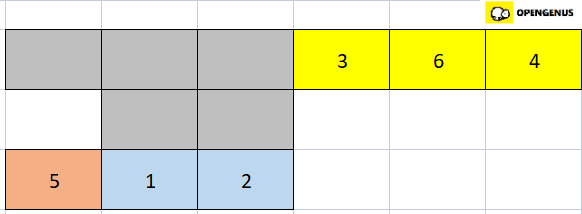
• So now we have to merge the left and right parts(that is the peach and blue part). For that we compare 5 with the first element of the blue array that is 1. Since 1 is smaller than 5 we place 1 at the first position of a new array.
  
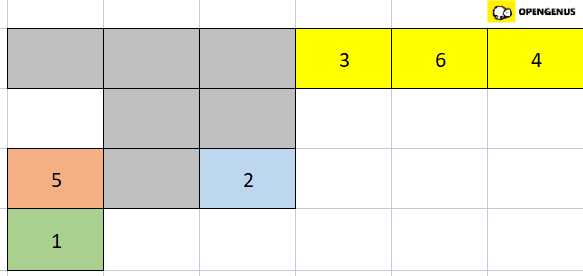
• Now we compare 5 with the second element of the blue array. Since 2 is smaller than 5, we place 2 and 5 in the second and third position of the new array respectively.
  
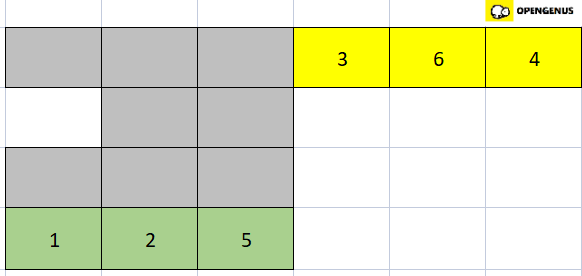
• Now the left half of the array is sorted, so we move to the right half of the array.
• We again divide it into single element arrays and single element arrays are already sorted.
  
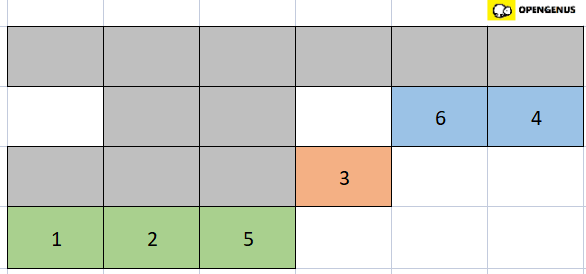
• We now sort the right half of the right half of the array(blue part).
  
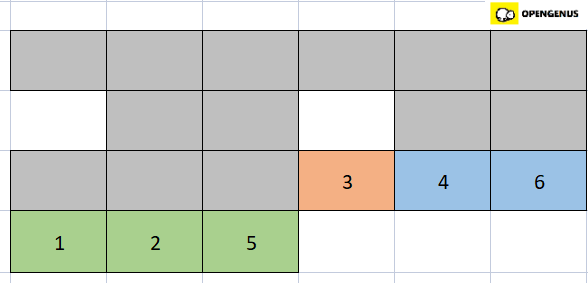
• Now we merge the left and right parts of the right half of the array (that is the peach and blue part).
• Comparing the first element of the peach part(that is 3) with the first element of the blue part(that is 4).3 is smaller so we place it in the first position of a new array and since the right part(blue part) of the right half of the array is already sorted we place the elements as it is in the new array.
  
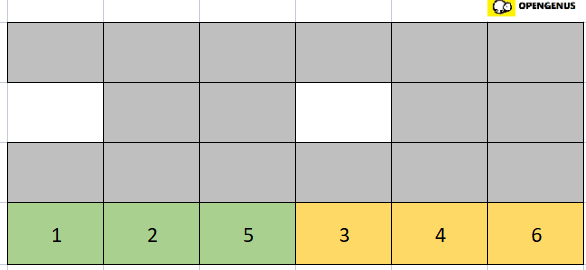
• The left and right halves of the array are now sorted so we merge these two together.
• Comparing the first element of the left half of the array(that is 1) with the first element of the right half of the array(that is 3). 1 is smaller so we place it in the first position(0th index) of a new hypothetical array.
  
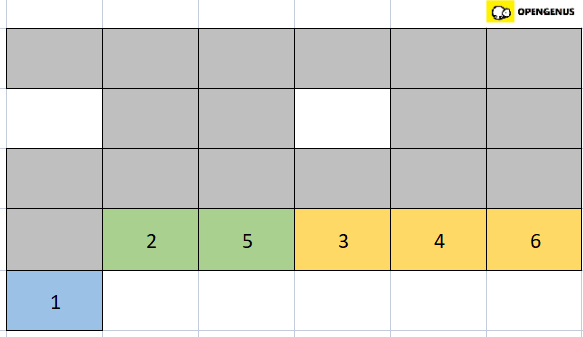
• Comparing the second element of the left half of the array(that is 2) with the first element of the right half of the array(that is 3). 2 is smaller than 3 so we place 2 in the second position(1st index) of the new array.
  
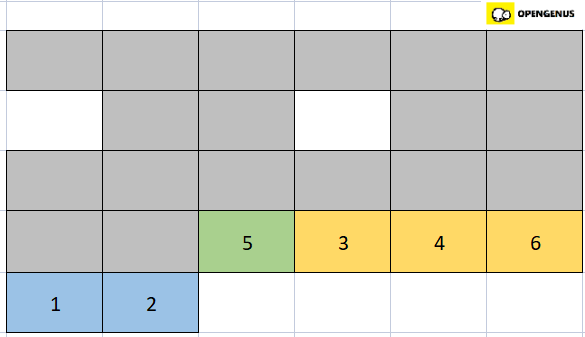
• Comparing third element of the right half of the array(that is 5) with the first element of the right half of the array(that is 3). 5 is greater than 3 so we place 3 in the third position(2nd index) of the new array.
  
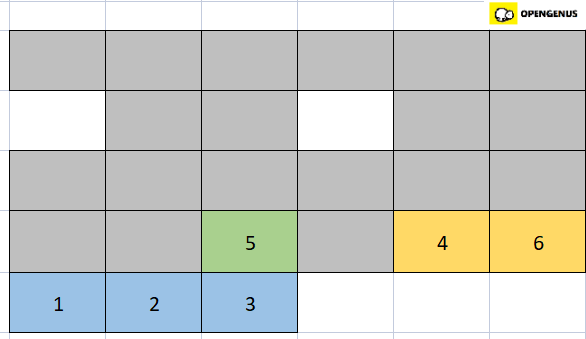
• Comparing third element of left half of the array(that is 5) with the second element of the right half of the array(that is 4). 5 is greater than 4 so we place 4 in the fourth position(3rd index) of the new array.
  
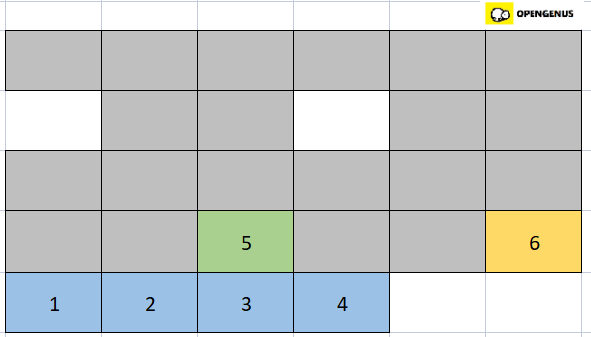
• Comparing third element of left half of the array(that is 5) with the thied element of the right half of the array(that is 6). 5 is smaller than 6 so we place 5 in the fifth position(4th index) of the new array.
  
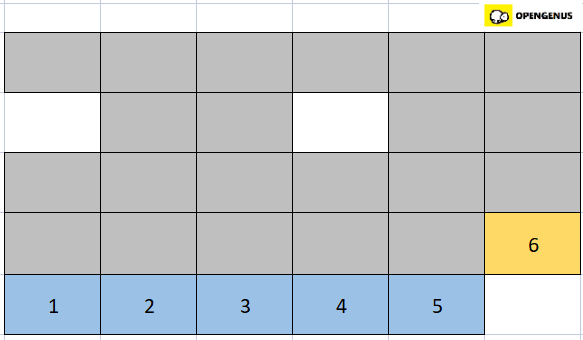
• Now only one element is left so we place it in the last position.
  
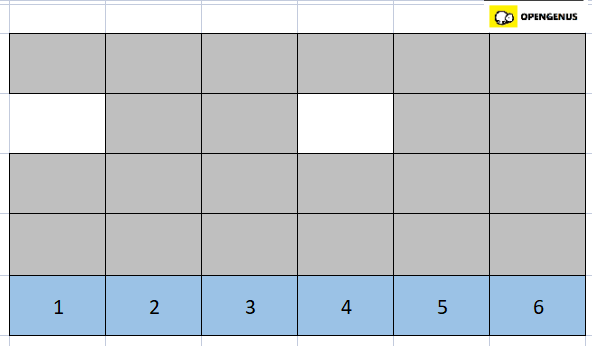
• The array is now sorted.

Approach to write the program

• In the main function, the function mergeSort
• In the function mergeSort we divide the array in two halves and then sort each half.
• Then we call the function merge.
• In merge, we create two temporary arrays and copy the data into it.
• Then we merge the two arrays back together.
• Then the function print is called, and the sorted array is printed.

Implementation

#include <stdio.h>
#include <stdlib.h>
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;
    int L[n1], R[n2];
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
    i = 0; 
    j = 0; 
    k = l; 
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}
//l is for left index and r is for right index
void mergeSort(int arr[], int l, int r)
{
    if (l < r) {
        int m = l + (r - l) / 2;
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
 
        merge(arr, l, m, r);
    }
}
void print(int A[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}
int main()
{
    int arr[] = {5, 2, 1. 3, 6, 4 };
    int arr_size = sizeof(arr) / sizeof(arr[0]);
 
    printf("Given array is \n");
    printArray(arr, arr_size);
 
    mergeSort(arr, 0, arr_size - 1);
 
    printf("\nSorted array is \n");
    print(arr, arr_size);
    return 0;
}

Output

Given array is 
5 2 1 3 6 4 

Sorted array is 
1 2 3 4 5 6

Time complexity

• The time complexity of merge sort algorithm is O(NlogN).

Benefits of Merge Sort

• Merge sort has a worst case time complexity of O(NlogN) which makes it quite suitable to work on large datasets.