
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 15 minutes
In this article, we have explored an insightful approach/ algorithm to find the largest island by changing one 0 to 1 in MxN matrix. This is an extension of Number of Islands in MxN matrix (of 0 and 1)
TABLE OF CONTENTS
- Pre-requisites
- Problem statement definition
- Problem analysis
- Solution analysis (algorithm)
- Psuedocode
- Implementation
- JAVA
- C++
- Complexity Analysis
- Time-Complexity
- Space-Complexity
- Applications
PRE-REQUISITES
Let us get started with Largest Island by changing one 0 to 1. This is similar to Leetcode problem 827, Making A Large Island.
PROBLEM STATEMENT DEFINITION
Imagine we have a 2D matrix of binary values (0s and 1s). We must change at most one 0 to a 1 such that we form the largest possible island of 1s in a sea of 0s.
PROBLEM ANALYSIS
What is an island?
In this particular question an island is a group of connected 1s. Take a look at the image below. Let the green squares represent 1s and the white squares represent 0s. The group of 1s surrounded by the white sea of 0s are an islands. We need to count the number of such clusters.
The program for solving this problem involves getting a 2D matrix of 0s and 1s as input.
For example, let the input be a 10 X 10 matrix: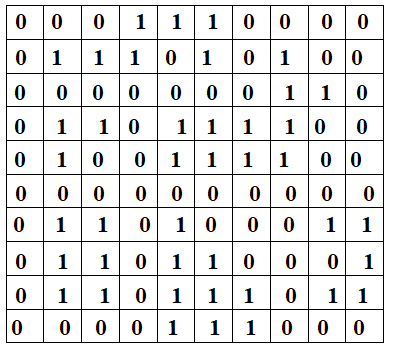
The islands of 1s are:
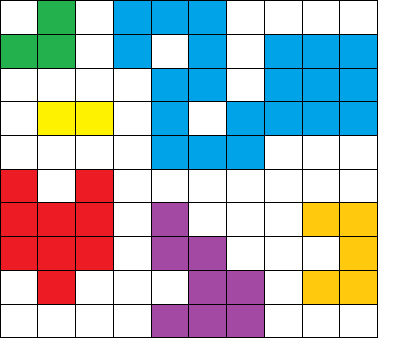
Finding the largest possible island changing one 0 to 1
Let us analyze all possible ways of changing one 0 to 1 to get a larger island.
The largest island is blue. So, intuitively we can see that it has to be part of the larger island(this point is important in the following solution to increase computational efficiency). Let us connect the blue with purple island.
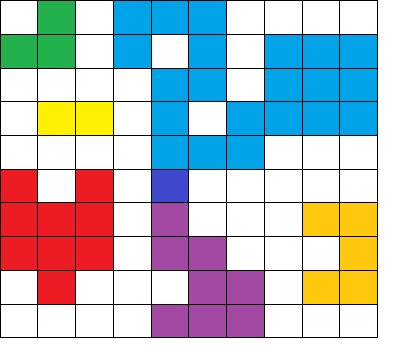
The area (number of 1s in the island) is 30. This is however, not the most efficient solution. We can connect three of the biggest islands (blue, green and red) by changing the 0 in between them to 1.
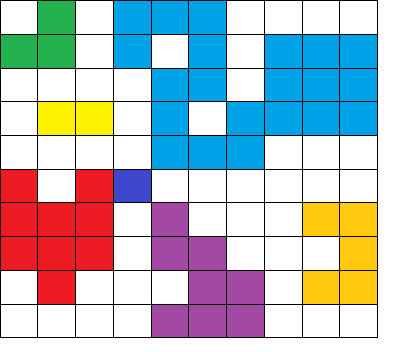
The area now is 39 and this is the largest possible island.
SOLUTION ANALYSIS (ALGORITHM)
The idea is simple. We first need to find all the islands in the matrix provided and paint it (This is an identifier that this island has been visited) using any of the approaches mentioned in the prerequisite article. For each 1 in the grid, we paint all connected 1 with the next available color (2, 3, and so on). We also remember the size of the island we just painted with that color.Then, we analyze all 0 in the grid, and sum sizes of connected islands (based on the island color). Note that the same island can connect to 0 more than once.
We also have to maintain a pointer array which points to the islands in decreasing order of area. For example, in the matrix provided above, the array would be pointing to {blue, red, purple, orange, green, yellow}. This extra storage simplifies our calculations and provides an order for our solution, so that we do not include the same island pair over and over again . We start with the largest island, check if we can connect it to the second largest island and so on. This solution must also tackle cases where it is possible to connect 3 or more islands with only one change.
We must maintain an result variable which is used to com pare the stored area and the current calculated area. If the latter is greater, we replace result with the new value. We then repeat this process for all islands and print the result as the largest possible area obtained after changing one 0 to 1!.
PSUEDOCODE
Solution:
def largestIsland(self, grid: List[List[int]]) -> int:
def valid(i, j):
return 0 if i < 0 or i >= len(grid) or j < 0 or j >= len(grid[0]) else grid[i][j]
def paint(i, j, color):
if valid(i, j) != 1: return 0
grid[i][j] = color
return 1 + paint(i+1, j, color) + paint(i-1, j, color) + paint(i, j+1, color) + paint(i, j-1, color)
# paint all island to different color
island = [0, 0] # color labeling starts from 2
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
island.append(paint(i, j, len(island)))
res = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if not grid[i][j]:
visited = set()
visited.add(valid(i+1, j))
visited.add(valid(i-1, j))
visited.add(valid(i, j+1))
visited.add(valid(i, j-1))
res = max(res, 1 + sum(island[color] for color in visited))
if (!res)
return len(grid)*len(grid[0])
else
return res
IMPLEMENTATION
JAVA Code:
class Solution {
public int largestIsland(int[][] grid) {
final int m = grid.length;
final int n = grid[0].length;
int maxSize = 0;
List<Integer> sizes = new ArrayList<>(Arrays.asList(0, 0));
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j] == 1) {
sizes.add(paint(grid, i, j, sizes.size())); // paint 2, 3, ...
}
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j] == 0) {
Set<Integer> neighborIds =
new HashSet<>(Arrays.asList(getId(grid, i - 1, j), getId(grid, i + 1, j),
getId(grid, i, j + 1), getId(grid, i, j - 1)));
maxSize = Math.max(maxSize, 1 + getSize(grid, neighborIds, sizes));
}
return maxSize == 0 ? m * n : maxSize;
}
private int paint(int[][] grid, int i, int j, int id) {
if (i < 0 || i == grid.length || j < 0 || j == grid[0].length)
return 0;
if (grid[i][j] != 1)
return 0;
grid[i][j] = id;
return 1 + paint(grid, i + 1, j, id) + paint(grid, i - 1, j, id) +
paint(grid, i, j + 1, id) + paint(grid, i, j - 1, id);
}
private int getId(int[][] grid, int i, int j) {
if (i < 0 || i == grid.length || j < 0 || j == grid[0].length)
return 0;
return grid[i][j];
}
private int getSize(int[][] grid, Set<Integer> neighborIds, List<Integer> sizes) {
int size = 0;
for (final int neighborId : neighborIds)
size += sizes.get(neighborId);
return size;
}
}
C++ Code
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int largestIsland(vector<vector<int>>& grid) {
const int m = grid.size();
const int n = grid[0].size();
int maxSize = 0;
vector<int> sizes{0, 0};
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j] == 1)
sizes.push_back(paint(grid, i, j, sizes.size()));
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j] == 0) {
const unordered_set<int> neighborIds{
getId(grid, i + 1, j), getId(grid, i - 1, j),
getId(grid, i, j + 1), getId(grid, i, j - 1)};
maxSize = max(maxSize, 1 + getSize(neighborIds, sizes));
}
if (maxSize == 0){
return m*n;
}
else{
return maxSize;
}
}
private:
int paint(vector<vector<int>>& grid, int i, int j, int id) {
if (i < 0 || i == grid.size() || j < 0 || j == grid[0].size())
return 0;
if (grid[i][j] != 1)
return 0;
grid[i][j] = id;
return 1 + paint(grid, i + 1, j, id) + paint(grid, i - 1, j, id)+ paint(grid, i, j + 1, id) + paint(grid, i, j - 1, id);
}
int getId(const vector<vector<int>>& grid, int i, int j) {
if (i < 0 || i == grid.size() || j < 0 || j == grid[0].size())
return 0;
return grid[i][j];
}
int getSize(const unordered_set<int>& neighborIds, const vector<int>& sizes) {
int size = 0;
for (const int neighborId : neighborIds)
size += sizes[neighborId];
return size;
}
};
int main(){
Solution ob;
vector<vector<int>> v ={{0,0,0,1,1,1,0,0,0},
{0,1,1,1,0,1,0,1,0},
{0,0,0,0,0,0,0,1,1},
{0,1,1,0,1,1,1,1,1},
{0,1,0,0,1,1,1,1,0},
{0,0,0,0,0,0,0,0,0},
{0,1,1,0,1,0,0,0,1},
{0,1,1,0,1,1,0,0,0}};
cout << "The largest island possible is: "<<(ob.largestIsland(v));
OUTPUT
The largest island possible is: 20
COMPLEXITY ANALYSIS
TIME COMPLEXITY
We use two loops to traverse across the matrix. Suppose there are n rows and m columns, then the time complexity is
Worst case time complexity: Θ(n^2)
- Average case time complexity:
Θ(n^2) - Best case time complexity:
Θ(n^2)
SPACE COMPLEXITY
The space complexity is proportional to the number of connected islands in the matrix, but at the worst case we have to store (n * m)/8 islands .
Hence the Space complexity is Θ(|number of connected islands|)
APPLICATIONS
- It is used in computational geometry and optical disproportionation problems
- An extension of this problem is used by photo editing software to fill in pixels in pictures with 'visual holes'.
