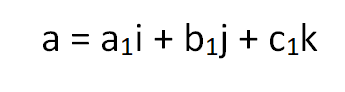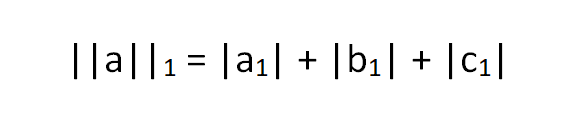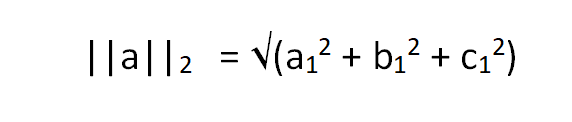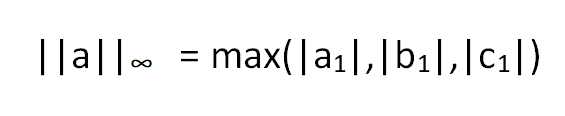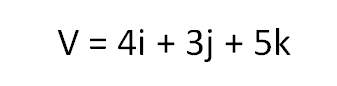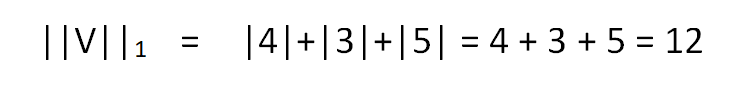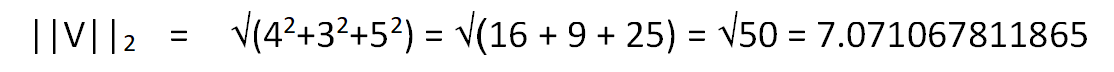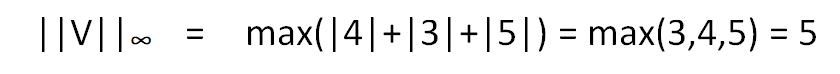In Machine learning, vectors and matrixes are used extensively to represent features, targets and other parameters and hyperparameters. Calculating the length or magnitude of the vector used in a particular model is often required in several matrix operations or direct implementations in regularization methods. The length of a vector is a positive integer, that speaks on the extent of the vector in space.

In this article, you will know about vector norm and the method to apply them in Python by using the Linear Algebra module of the NumPy library.
In general, three types of norms are used,

1. L1 norm
2. L2 norm
3. Vector Max Norm

L1 Norm

This one is also known as "Taxicab Norm" or "Manhattan Norm", represented as
||V||1 ,where V is the representation for the vector. L1 norm is the sum of the absolute value of the scalars it involves, For example,
Suppose you have vector a,

Then the L1 norm can be calculated by,

where |x| is the magnitude of x. Mathematically, it's same as calculating the Manhattan distance of the vector from the origin of the vector space.
In python, NumPy library has a Linear Algebra module, which has a method named norm(), that takes two arguments to function, first-one being the input vector v, whose norm to be calculated and the second one is the declaration of the norm (i.e. 1 for L1, 2 for L2 and inf for vector max).

from numpy import array  
from numpy.linalg import norm 
v = array([1,2,3])
l1 = norm(v,1)
print(l1)

OUTPUT

6.0

L2 Norm

This one is also known as "Euclidian Norm", represented as ||V||2, where V is the representation for the vector. L1 norm is the square root of the sum of the squares of the scalars it involves, For example,
For the same vecor as above, vector, L2 norm can be calculated by,

Mathematically, it's same as calculating the Euclidian distance of the vector coordinates from the origin of the vector space, resulting in a positive value.
You can use NumPy for this purpose too.

from numpy import array  
from numpy.linalg import norm 
v = array([1,2,3])
l2 = norm(v,2)
print(l2)

OUTPUT

3.7416573867739413

Vector Max Norm

Vector Max norm is the maximum of the absolute values of the scalars it involves, For example,
The Vector Max norm for the vector a shown above can be calculated by,

where |x| is the magnitude of x. Mathematically, it's same as calculating the maximum of the Manhattan distances of the vector from the origin of the vector space.

from numpy import array,inf
from numpy.linalg import norm 
v = array([1,2,3])
vecmax = norm(v,inf)
print(vecmax)

OUTPUT

3.0

A Mathematical Illustration

Suppose, we have a vector V, represented with the help of it's unit vectors in the vector space,

where i, j, k are the unit vectors along x-axis, y-axis and z-axis respectively.
So let's calculate norms manually.

For L1 norm, we need to calculate the distance of each component of the vector along x,y,z-direction from the origin of the vector space, i.e. from O(0,0,0).
Hence we get,

Similarly for L2 norm, we need to follow the Euclidian approach, i.e unlike L1 norm, we are not supposed to just find the component-wise distance along the x,y,z-direction. Instead of that we are more focused on getting the distance of the point represented by vector V in space from the origin of the vector space O(0,0,0).
So we get,

Vector Max Norm is an important concept, which is just concerned about the maximum manhattan distance of any conponent of the vector V in the respective directions, from the vector space. Hence we get,

Uses in Machine Learning Models

There are numerous instances in machine learning where we need to represent the entire data set with the help of a singele interger for better comprehension and modeling of the input data. For example,

1. While dealing with data set in multiple dimension, like RGB matrix in image processing or face detection,for a single data point we are supposed to use it's magnitude in many dimensions. In that case norm (especially vector max norm) plays a greater role.
2. Almost all Machine Learning models provide some error, no one can predict the 100% accurate data. For the representations of errors or average error or the maximum possible error in machine learning modeling we use norm for the error matrix.
3. It may be a regression model or a classification model, there always exists some loss function, that calculates the loss of the same model. We use norm to represent the loss of a model too.
4. Most of the time, norm helps in vizualising the model in a proper way and evaluate it.
5. For many input data (like the data used in Reinforcement Learning Models), we use norm to squeeze the information to a single number, that can further take part in prediction. This depends on the data that has been used as input data.

With this article at OpenGenus, you must have the complete idea of .norm() method of Numpy library in Python. Enjoy.