
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes
Given a directed graph, we need to find the number of paths with exactly k edges from source u to the destination v.
We will solve this using three approaches:
- Brute force O(V^K) time
- Dynamic Programming O(V^3 * K) time
- Divide and Conquer O(V^3 * logK) time
The key idea to solve this problem is that we need to begin with the adjacency matrix adj and raising it to a power of K gives the value within adjacency matrix as the path of length K.
We use adjacency matrix of the given graph in which value of adj[i][j] represents if there is an edge from vertex i to vertex j in the graph. If the value is 1 then there is an edge from vertex i to vertex j else, if value is 0 then there is no edges from vertex i to vertex j in the graph.
To understand the problem let's take an example of a graph with 6 vertices {0, 1, 2, 3, 4, 5} and edges. Now let's find number of paths from vertex 0 to vertex 2 with 2 edges. Below a diagram of the graph is given:
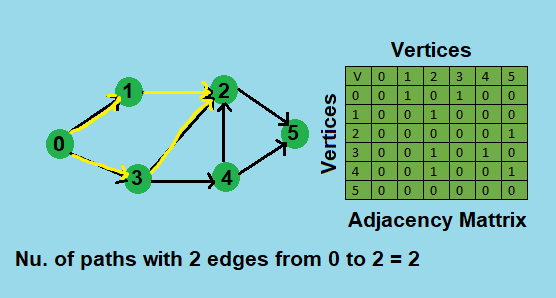
From the above graph we can conclude that there are 2 paths from vertex 0 to vertex 2 with 2 edges, one is 0-->1-->2 and the other is 0-->3-->2. The same we can find by the analysis of adjacency matrix of the graph.
To solve this problem, we will see three approaches.
- First one is naive or brute force approach which takes O(Vk) time
- second one is Dynamic programming approach which takes O(V3k) time
- the last is Divide and Conquer approach which takes O(V3log k) time.
Naive approach (Brute Force)
This is the simple way to start from the source, go to all the adjacent vertices and recur for adjacent vertices for k as k-1, source as adjacent vertices. When k becomes 0 and we reach to the destination, then we count it as one of the solution.
int numberOfPathsNaive(std::vector< std::vector<int> > adj, int u, int v, int k)
{
int __v = adj.size();
if(k == 0 && u == v)
return 1;
if(k == 1 && adj[u][v])
return 1;
if(k <= 0)
return 0;
int res = 0;
for(int i = 0; i < __v; ++ i)
{
if(adj[u][i])
{
res += numberOfPathsNaive(adj, i, v, k - 1);
}
}
return res;
}
The naive approach takes O(Vk) time as in the adjacency matrix we check each and every vertices for a path this takes O(V) time each, and we do the this k times. The worst occurs for a complete graph when for each vertex there are V edges going out from them.
Dynamic Programming approach
In dynamic programing approach we use a 3D matrix table to store the number of paths, dp[i][j][e] stores the number of paths from i to j with exactly e edges.
We fill the table in bottom up manner, we start from e=0 and fill the table till e=k. Then we have our answer stored in dp[u][v][k] where u is source, v is destination and k is number edges between path from source to destination.
Here we use the recurrence as:
if(e>1)
for(int b = 0; b < __v ; ++b)
if(adj[i][b])
dp[i][j][e] += dp[b][j][e - 1];
The time complexity of DP approach is O(V3k).
Implementation
Code in C++11
// C++ Program to find the number of paths
// with k edges from source to dest with DP appraoch.
#include<iostream>
#include<vector>
int numberOfPathsdp(std::vector<std::vector<int>> adj, int u, int v, int k)
{
int __v = adj.size();
int dp[__v][__v][k + 1];
for(int e = 0;e <= k; ++ e)
{
for(int i = 0;i < __v; ++ i)
{
for(int j = 0;j < __v; ++ j)
{
// initialize
dp[i][j][e] = 0;
// base cases
if(e == 0 && i == j)
dp[i][j][e] = 1;
if(e == 1 && adj[i][j])
dp[i][j][e] = 1;
// go to adjacent edges only when number of edges is more than 1
if(e>1)
{
for(int b = 0; b < __v ; ++ b)
{
if(adj[i][b])
{
dp[i][j][e] += dp[b][j][e - 1];
}
}
}
}
}
}
// number of paths from u to v with k edges
return dp[u][v][k];
}
int main()
{
int _v, e;
std::cin >> _v >> e;
std::vector< std::vector<int> > adj(_v, std::vector<int>(_v));
int u, v;
for(int i = 0;i < e; ++ i)
{
std::cin >> u >> v;
adj[u][v] = 1;
}
int k;
std::cin >> u >> v >> k;
int res = numberOfPathsdp(adj, u, v, k);
std::cout << res << "\n";
return 0;
}
Divide and Conquer approach
We can use divide and conquer approach to solve this problem in O(V3log2k) time, to this we use the fact that the number of paths of length k from u to v is the [u][v]th entry in the matrix (adj[V][V])k.
The kth power of a graph G is a graph with the same set of vertices as G and an edge between two vertices iff there is a path of length at most k between them. Since a path of length two between vertices u and v exists for every vertex w such that {u,w} and {w,v} are edges in G, the square of the adjacency matrix of G counts the number of such paths. Similarly, the [u][v]th element of the kth power of the adjacency matrix of G gives the number of paths of length k between vertices u and v.
To find (adj[V][V])k we use the divide and conquer approach of finding power(x, y) in O(log2y) time, i.e. this algorithm is an application of fast matrix exponentiation.
// Function to compute adj raise to power k.
int power(std::vector<std::vector<int>> adj, int u, int v, int k)
{
int __v = adj.size();
std::vector<std::vector<int>> res(__v, std::vector<int>(__v));
for(int i = 0; i < __v; ++i)
res[i][i] = 1;
while (k > 0)
{
if (k % 2 == 1)
res = multiply(res, adj);
adj = multiply(adj, adj);
k /= 2;
}
// number of paths from u to v with k edges
return res[u][v];
}
Implementation
Code in C++11
// C++ Program to find the number of paths
// with k edges from source to dest with Divide and Conquer appraoch.
#include <iostream>
#include <vector>
// A utility function to multiply two matrices
// a[][] and b[][]. Multiplication result is
// stored back in a[][]
std::vector<std::vector<int>> multiply(std::vector<std::vector<int>> a,
std::vector<std::vector<int>> b)
{
// Creating an auxiliary matrix to store elements
// of the multiplication matrix
int __v = a.size();
std::vector<std::vector<int>> mul(__v, std::vector<int>(__v));
for (int i = 0; i < __v; ++i)
{
for (int j = 0; j < __v; ++j)
{
mul[i][j] = 0;
for (int l = 0; l < __v; ++l)
mul[i][j] += a[i][l] * b[l][j];
}
}
return mul;
}
// Function to compute adj raise to power k.
int power(std::vector<std::vector<int>> adj, int u, int v, int k)
{
int __v = adj.size();
std::vector<std::vector<int>> res(__v, std::vector<int>(__v));
for(int i = 0; i < __v; ++i)
res[i][i] = 1;
while (k > 0)
{
if (k % 2 == 1)
res = multiply(res, adj);
adj = multiply(adj, adj);
k /= 2;
}
// number of paths from u to v with k edges
return res[u][v];
}
// function to find total number of paths
// with k edges.
int numberOfPathsDivideConquer(std::vector<std::vector<int>> adj, int u, int v, int k)
{
return power(adj, u, v, k);
}
int main()
{
int _v, e;
std::cin >> _v >> e;
std::vector<std::vector<int>> adj(_v, std::vector<int>(_v));
int u, v;
for (int i = 0; i < e; ++i)
{
std::cin >> u >> v;
adj[u][v] = 1;
}
int k;
std::cin >> u >> v >> k;
int res = numberOfPathsDivideConquer(adj, u, v, k);
std::cout << res << "\n";
return 0;
}
Complexity
Time Complexity
- Brute force approach takes O(Vk) time.
- DP approach takes O(V3k) time.
- Divide and Conquer approach takes O(V3log2k) time.
Space Complexity
- Brute force approach takes O(V2) auxiliary space and O(Vk) stack space.
- DP approach takes O(V2k) auxiliary space.
- Divide and conquer takes O(V2) auxiliary space.
