
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 10 minutes
A treap is a height balanced binary tree. It is used to store a sequence in a tree, which allows for various applications like searching. A Cartesian tree, in case of a sorted sequence, would be basically a linked list, making tree virtually useless. Treap is used to solve such cases by using random priority for each node.
Thus treap is a balanced binary tree with heap properties.
A treap node stores 2 values:
- Key (Sequence element)
- Priority
A treap is built in such a way that it is essentially a binary search tree for Keys, i.e. the sequence elements and a heap for priorities. So a treap follows following properties:
- Priority of a node is always greater than its children.
- The key of a node is greater than the key stored in its left child.
- The key of a node is lower than the key stored in its right child.
The priority for each sequence element is chosen randomly. The insertion process is essentially to create a node as leaf with random priority and perform tree rotations to repair any violations of heap property.
Tree rotation operation:
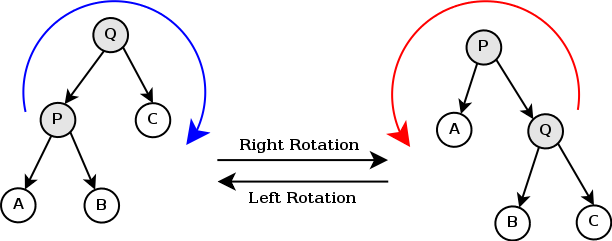
In the above image, A, B, C are subtrees, while P and Q are two nodes that are target of rotation. The left image shows right rotation of node P while image on right shows right rotation of node Q. These two operations are inverse of each other.
A treap is expected to perform three major operations:
- Search
- Insert
- Delete
Inorder traversal of a treap would give the sorted sequence.
Algorithm
Insert operation
Insert operation is done for the whole sequence to build the tree.
1. Create new node with the given key value x and random priority value.
2. Start from root and perform search for x by using key values to perform
a binary search. When a leaf node is reached, insert new node at the
leaf. This is basically a binary search tree insertion.
3. Rotate up to make sure heap property is satisfied with respect to
priority values.
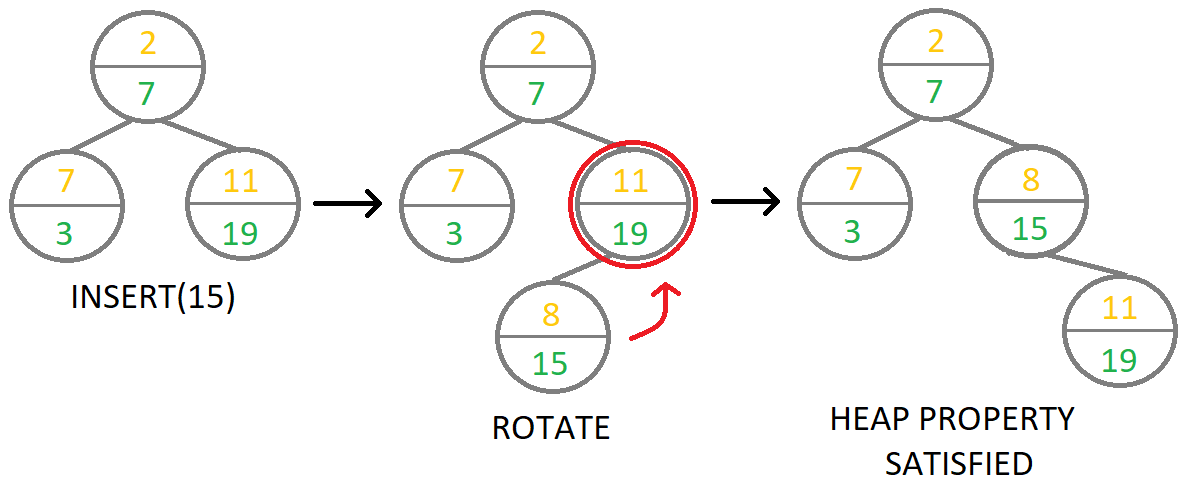
The image above shows insert operation for key 15. Green values in nodes are keys and orange values are priorities. Priority of 8 is assigned to node with key 15 randomly.
Search operation
Search operation is same as search in binary search tree since rotation maintains BST property.
1. Start from root to search for a key x.
2. Compare key of the node. If key is equal to x, return the node.
3. If key is less than x go to right child and repeat step 2.
4. If key is greater than x go to left child and repeat step 2.
5. If key is not equal to x and node has no children, then x is not
present in tree.Delete operation
1. Search for the node to be deleted.
2. If the node is at leaf, delete it directly.
3. Otherwise, set the node to lowest priority and perform rotations until
heap property of tree is satisfied.
4. Delete the node when it is at leaf.
For step 3, if tree is a max heap, set node's priority to negative infinity and
if tree is a min heap, set priority to infinity.
Complexity
$\bf{Space \hspace{1mm }complexity:}\hspace{1mm} O(N)$
$\bf{Time\hspace{1mm }complexities:}$
- $\bf{Search:} \hspace{1mm} O(log_2{N})$
- $\bf{Insert:} \hspace{1mm} O(log_2{N})$
- $\bf{Delete:} \hspace{1mm} O(log_2{N})$
Implementations
C++ 11
/*
* c++ 11 code to construct a Treap. Inorder traversal gives a sorted array.
*/
#include <iostream>
#include <vector>
#include <climits>
#include <cstdlib>
struct Node{
int key, priority;
Node *left, *right;
Node(int x){
key = x;
priority = rand() % 10000;
left = right = NULL;
}
};
class Treap{
private:
Node *root;
Node * rotateLeft(Node *p){
Node *q = p->right;
p->right = q->left;
q->left = p;
return q;
}
Node * rotateRight(Node *q){
Node *p = q->left;
q->left = p->right;
p->right = q;
return p;
}
Node * insert(Node *sub_tree, int key){
// If leaf is reached
if(sub_tree == NULL)
return new Node(key);
if(sub_tree->key < key){
// Run insert for right sub-tree
sub_tree->right = insert(sub_tree->right, key);
// Check if right subtree satisfies min-heap property
if(sub_tree->right->priority < sub_tree->priority){
// Perform left rotate
sub_tree = rotateLeft(sub_tree);
}
}
else{
// Run insert for left sub-tree
sub_tree->left = insert(sub_tree->left, key);
// Check if left subtree satisfies min-heap property
if(sub_tree->left->priority < sub_tree->priority){
// Perform right rotate
sub_tree = rotateRight(sub_tree);
}
}
return sub_tree;
}
Node * search(Node *sub_tree, int key){
if(sub_tree == NULL)
return NULL;
if(sub_tree->key == key)
return sub_tree;
else if(sub_tree->key < key){
return(search(sub_tree->right, key));
}
else return(search(sub_tree->left, key));
}
void inorderTraversal(Node *node){
if(node == NULL)
return;
inorderTraversal(node->left);
std::cout << node->key << ' ';
inorderTraversal(node->right);
}
public:
Treap(){
root = NULL;
}
void insert(int x){
root = insert(root, x);
}
void Search(int x){
Node *temp = search(root, x);
if(temp == NULL)
std::cout << "Key not found\n";
else
std::cout << "Key found with priority " << temp->priority
<< '\n';
}
void inorderTraversal(){
inorderTraversal(root);
}
};
int main() {
std::vector<int> ar = {5, 4, 3, 2, 1};
Treap tree;
for(auto x : ar)
tree.insert(x);
tree.inorderTraversal();
std::cout << '\n';
}Applications
- Treap is used as a self balancing binary tree.
- Treap is used to solve connectivity problems.
References/ Further reading
- Wikipedia article on Treap
- Read about red-black tree: a simpler data structure that does the same task as a treap.
