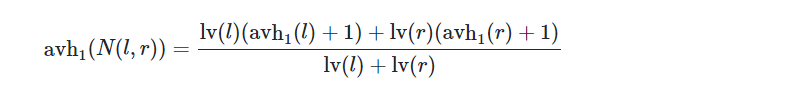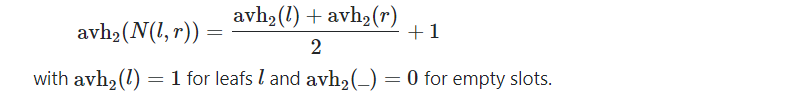Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 25 minutes
In this article, we have explored an insightful approach/ algorithm to find the average height of nodes in the given Binary Tree. This will strengthen our understanding of binary trees and their applications.
Pre-requisite: Average height of Random Binary Tree
Before we move further into the topic of discussion, let us revise the basics of a binary tree!
TABLE OF CONTENTS
- Points to recall
- Size of a binary tree
- Height in a binary tree
- Understanding the problem
- Approach-1
- Algorithm
- Implementation
- Time-Complexity Analysis
- Space-Complexity analysis
- Approach-2
- Algorithm
- Implementation
- Time-Complexity Analysis
- Space-Complexity analysis
- Comparison of approaches
- Test your Understanding
1) POINTS TO RECALL
This article only brushes over concepts of a binary tree that are required in the solution of the problem statement. Learn more from the Binary Tree article from OpenGenus.
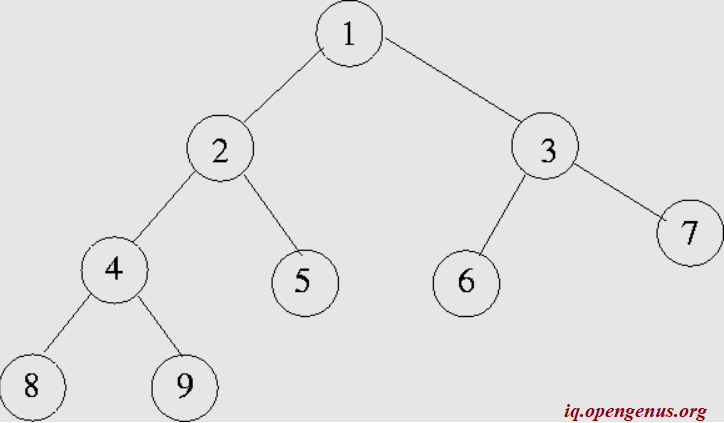
A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.
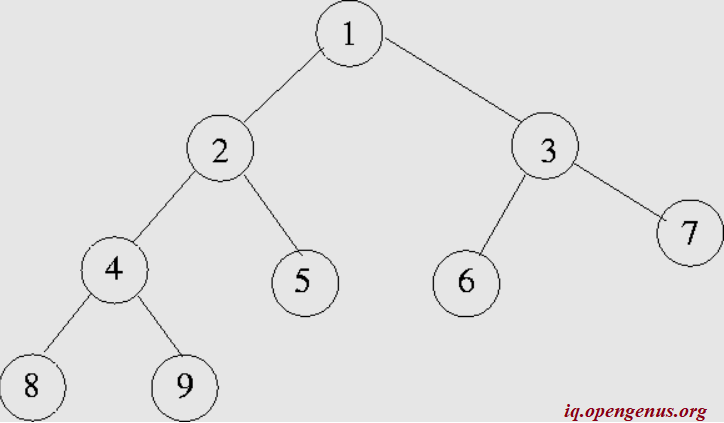
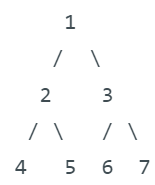
In the above example, node 1 is the root. There are 9 nodes in all and each node has either 0 or 2 child nodes.
1.1) Size of a binary tree:
The size of a binary tree is simply the number of nodes present. In the above example, the number of nodes are 9 and it is the size of the binary tree.
1.2) Height in a binary tree:
With respect to a binary tree, height can be defined at two level - node and the entire tree.
- Height of a node: The height of a node is defined by the following relation:
height(leaf_nodes) = 1
height(internal_nodes) = 1 + max{(height(t1), height(t2)},
where t1 = left_subtree and t2 = right_subtree.
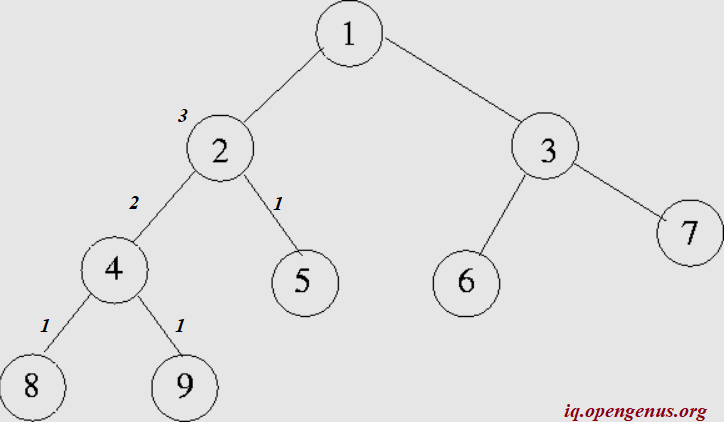
Let us consider an example. In the above figure, let us find the height of node 2.
Node 2 is not a leaf node, so condition 2 is applied. THe left and right sub_tree are defined:
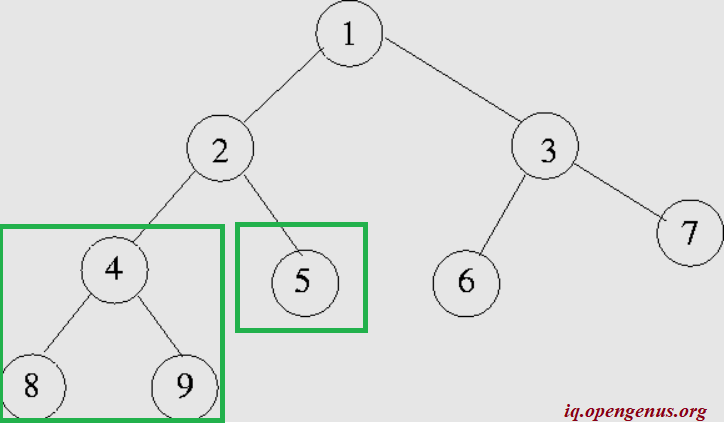
The root of the left-subtree(node 4) is not a leaf-node, so it is further split:
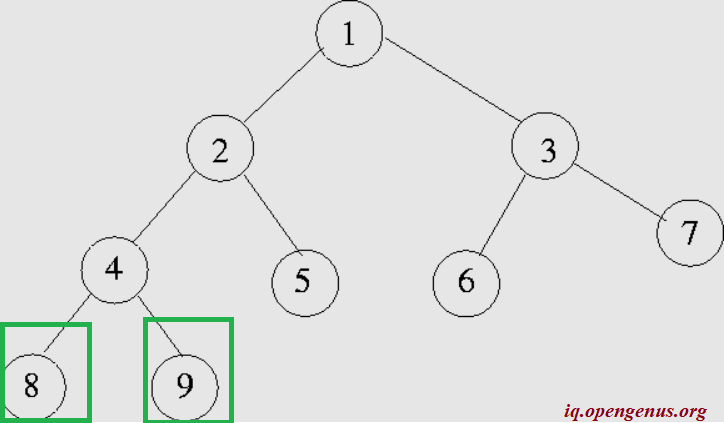
Now, we have the leaf_node, let us mark their height.
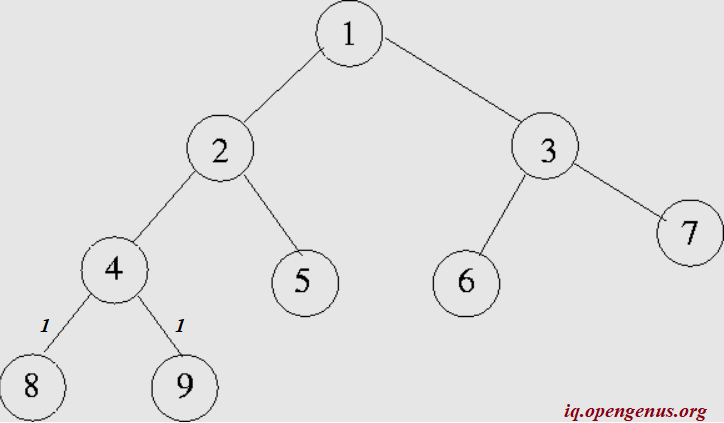
From this the height of the node 4 is 1+max(1,1) = 2.Similarly the height of node 5 is 1. Since we have the height of pre-requisite nodes, the height of node 2 can be calculated as
1+ max(height(left_subtree), height(right_subtree)
1+ max ( 2,1)
1+ 2 = 3
- Height of the binary tree: The height of a binary tree is the height of the root node in the whole binary tree. In other words, the height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.
Let us find the height of the example binary tree by first applying condition 2.
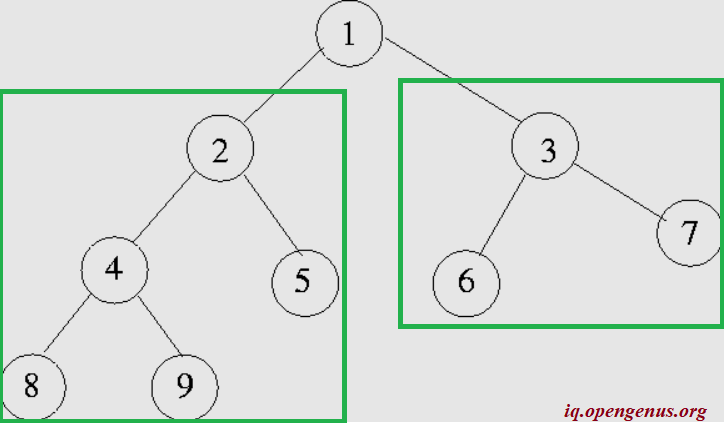
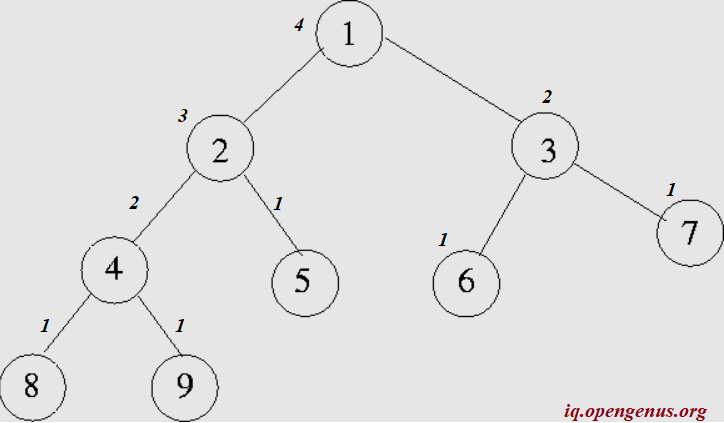
We are aware from our previous section that the height of the left_subtree is 3. Let us calculate the height of the right sub_tree (node 3). It is = 1+ max (1,1) =2
Hence, the height of the binary tree is
1 + max (3,2) =
1 + 3 = 4
Note: If all that we know about a binary tree is that there are n nodes in it, the tree can be constructed in many ways such that the height of the tree ranges from n-1 to floor(log n).
i.e maximum height of the binary tree of n nodes is n-1 and minimum height is floor(log2n)
Now that we understand how to calculate the height, let us move on to the problem at hand!
2) UNDERSTANDING THE PROBLEM:
The problem statement is simple: We need to find the Average height of the Binary Tree. The structure of the problem looks like this:
Input: The binary tree is given as the input
Output: We need to print the average height of that particular tree
Computation Involved: Finding the average height of all nodes in the tree
Let us take an example to understand this problem.
Let us consider the same example as before.
We know the heights of all the node:
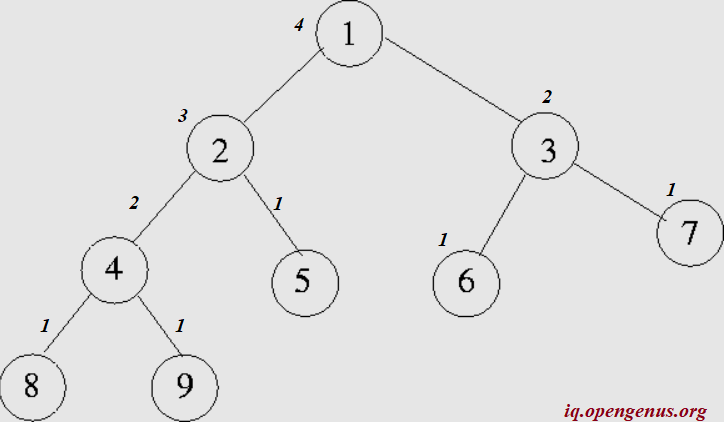
This problem involves calculating the average height of all nodes in the tree. Quantitatively, it is (1+1+1+1+1+2+2+3+4)/9 = 1.78.
This problem can be easily solved using two approaches:
3) APPROACH-1
Algorithm:
The natural solution might be to take the average length of all possible paths from the root to a leaf, that is:
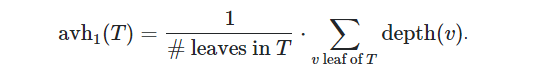
Implementation
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node* left;
struct Node* right;
Node(int val)
{
data = val;
left = NULL;
right = NULL;
}
};
double avg_ht(Node root, int visited){ // visited is an array which marks the leaf nodes initialized with 0s
double ht = 0.0;
int n = sizeof(visited)/sizeof(visited[0]);
if (root == NULL)
return ht/n;
else if (root->left!=NULL){
ht++;
visited[root->left.data]=1
avg_ht(root->left, visited);
}
else if (root->right!=NULL){
ht++;
visited[root->right.data]=1
avg_ht(root->tight, visited);
}
else{
return ht/n;
}
}
Time-Complexity
It takes logn time at the worst case for the recursive function to generate the height of a node and there are n nodes in all.
- Worst case time complexity:
Θ(n * log n) - Average case time complexity:
Θ(n * log n) - Best case time complexity:
Θ(n * log n)
Space-Complexity
We do not use any auxiliary space in this algorithm. Hence,
- Space complexity:
Θ(1)
4) APPROACH-2
Algorithm
Another option is recursive definition, that is the average height for a node is the average over the average heights of the subtrees plus one, that is
This method eliminates inefficient recursive cycles to calculate the height of each node.
Implementation:
namespace AverageHeight
{
public class tree
{
public tree left;
public tree right;
}
class Program
{
static int count = 1;
static void Main(string[] args)
{
var tree = new tree()
{
left = new tree() { left = new tree(), right = new tree() },
right = new tree() { left = new tree(), right = new tree() }
};
var avg = (decimal)Height(tree, 0) / count;
}
static int Height(tree t, int l)
{
if (t.left != null) count++;
if (t.right != null) count++;
return l + (t.left != null ? Height(t.left, l + 1) : 0) +
(t.right != null ? Height(t.right, l + 1) : 0);
}
}
}
Time-Complexity
It takes logn time at the worst case for the recursive function to generate the height of all nodes
- Worst case time complexity:
Θ(log n) - Average case time complexity:
Θ(log n) - Best case time complexity:
Θ(log n)
Space-Complexity
We do not use ant auxiliary space in this algorithm. Hence,
- Space complexity:
Θ(1)
4) COMPARISON OF APPROACHES
| APPROACH | TIME-COMPLEXITY | SPACE-COMPLEXITY |
|---|---|---|
| Approach-1 | n * logn | 1 |
| Approach-2 | logn | 1 |
5) TEST YOUR UNDERSTANDING
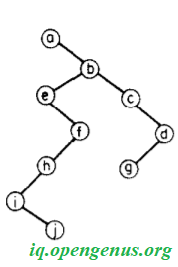
What is the height of the binry tree given below?
Thus the average height = (4+4+3)/7
= 11/7
= 1.57
With this article at OpenGenus, you now know how to find the average height of the given binary tree!