Consistent Hashing is a distributed hashing scheme that operates independently of the number of servers in a distributed hash table.

Table of contents:

1. Hashing
2. Hash Table
3. Consistent Hashing

Prerequisite: Distributed hash table, Hashing

Prior to discussing Consistent Hashing, let us describe what Hashing is.

Hashing

Hashing is the process of transforming a given key into a code with a hash function. A more specific definition of hashing is the practice of taking a string or input key, a variable used to store narrative data, and constructing a hash value. This is typically determined by an algorithm, and yields a shorter string than the original.
Hash Tables use hashing internally.Data in hash tables is stored as key-value pairs. The key, which identifies the data, is used as input to the hashing function.The hash code, which is an integer, is then mapped to the fixed size we have.

Hash Table

Hash tables are data structures that implement an associative array abstract data type, a structure that maps keys to values. Hash tables use a hash function to calculate an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.Hash tables are known for their constant lookup times.

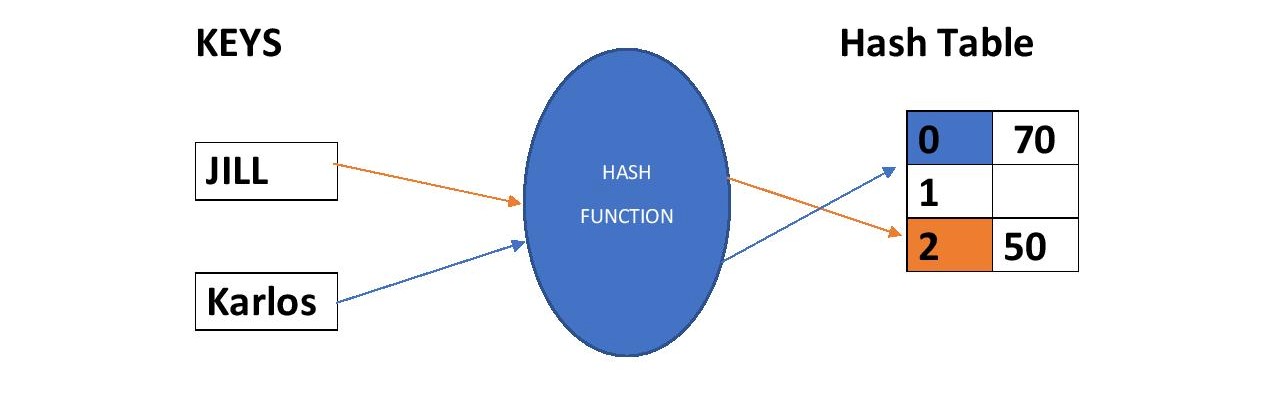
Let's consider the above image , we can clearly see that when the Hash Function is applied on those keys , it gives the index at which the value for that key is stored. If we want to add new Key , Value pair in this Hash Table , First the key is supplied to the Hash Function which generates its HashCode , this HashCode can be used to store the value.

Consistent Hashing

Before we talk on Consistent Hashing , Let's talk about how can hashing be used to map user or program requests over a network of servers. Consider we have 3 servers, these servers serve user requests for say a social media website like Facebook etc.
Now let's consider user requests to be u0 , u2 , u3 .... ,u8. The question that arises now is that how would you map these requests to these servers?. One could say we could use a hashing function to map these requests to each server.let's use modulo(%) Operator as our Hashing Function.

Hash Function H(ui) = i % N (N being the Number of servers)
Using the Hashing Function we get the following mapping:(N = 3)

u0 , u3 , u6 --- Server 0
u1 , u4 , u7 --- Server 1
u2 , u5 , u8 --- Server 2

What if a server goes down? Speaking realistically , we don't know when a server might go down. What if we want to add more servers? Let's see what will happen to all the request mappings if we change the number of servers. When we add or remove a new server , the value of N will change. This will result in our old hash function also changing. New Mappings when a server is added.

u0 , u4 , u8 --- Server 0
u1 , u5      --- Server 1
u2 , u6      --- Server 2
u3 , u7      --- Server 3

To the naked eye everything seems relatively well distributed, but on a close examination , we see that the mapping for most of the requests have changed. This will result in huge amount of work to reshuffle all the data around the servers.
What typically happens in servers is that we know which user might send requests to this server via the user request id , we can optimize the performance of the server by locally caching the data for regular users thus reducing the time to serve each request. This caching of data becomes useless and the load upon each server increases. Thus simple Hashing in Load balancing is not idea. This is where Consistent Hashing steps in.

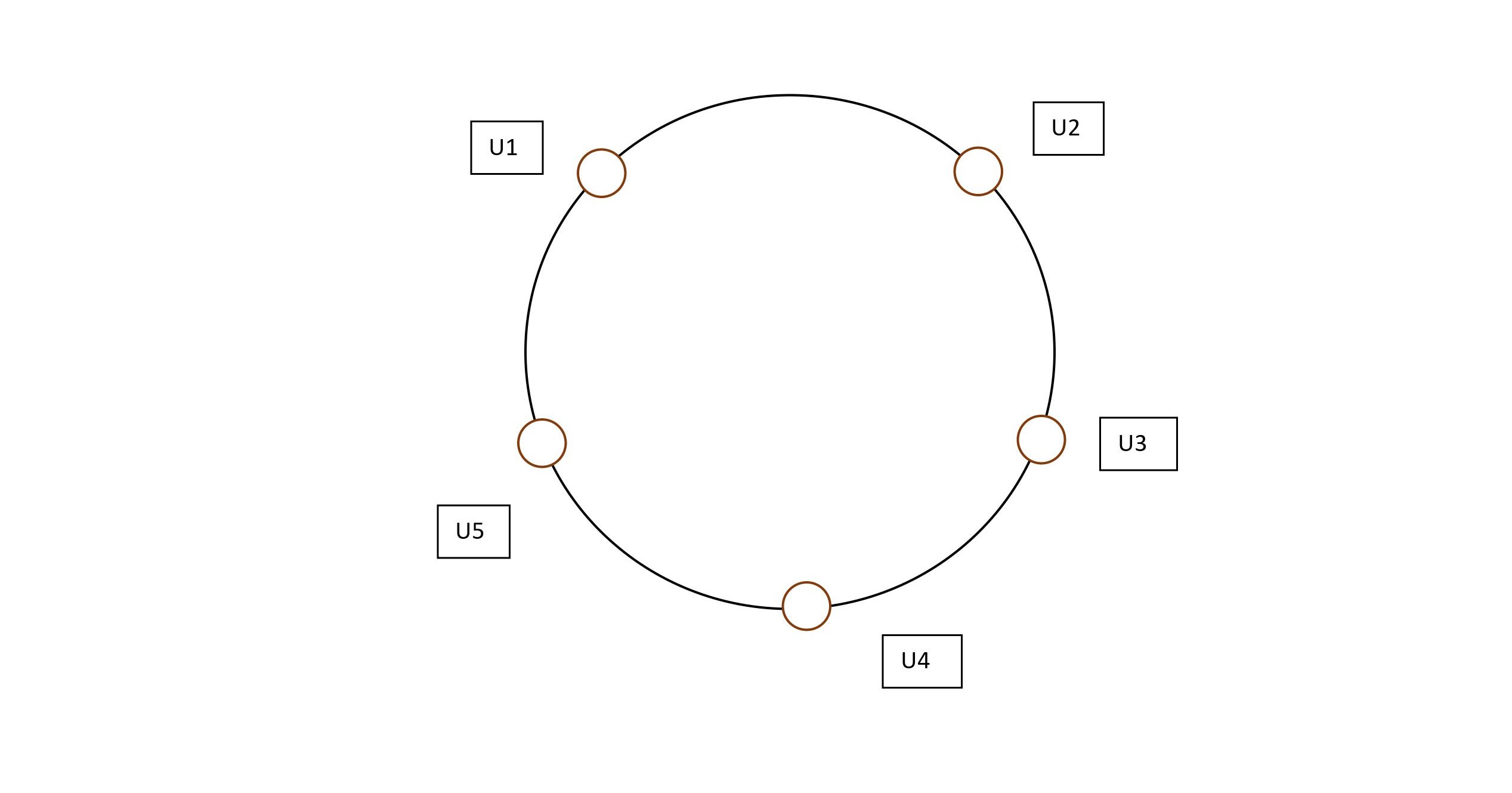
Consistent Hashing was designed to mitigate the problem where each request had to be mapped again. It is a distributed hashing scheme that operates independently of the number of servers in a distributed hash table. Imagine we map the hash output range onto the edge of a circle. Our minimum possible hash would be Zero , it shall correspond to angle zero and the maximum hash is dependent on the number of requests we have , which would in a real world scenario be a large number but for the simplicity's sake let's consider this to be a small number.

No of Servers -> 3 (S1 , S2 , S3)
No of Users -> 5 (U1 , U2 , U3 , U4 , U5)
let's place these users on the edge of the circle. The Resultant figure would look like :

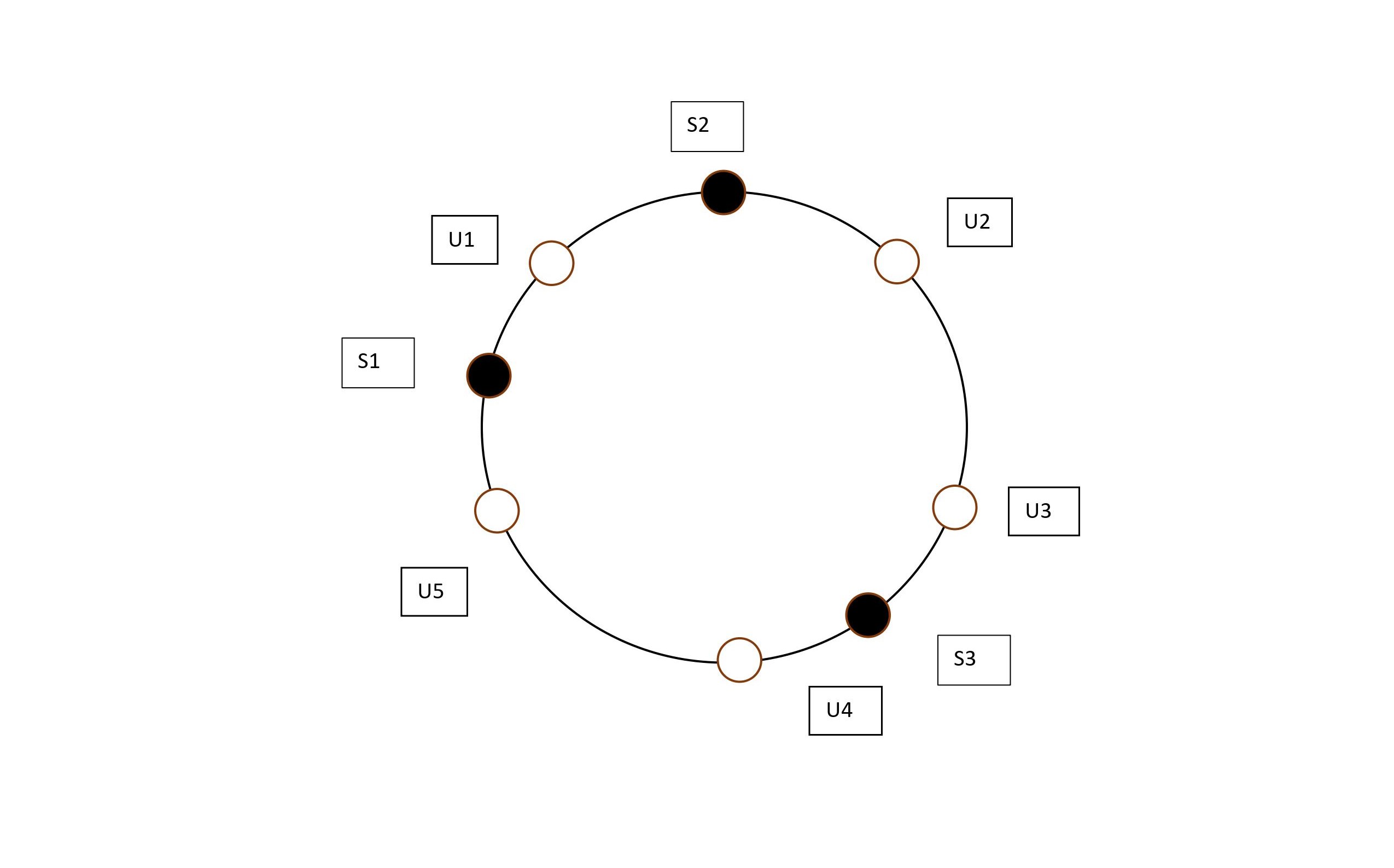
Now imagine we're placing these servers onto the edge of the circle , by assigning them pseudo-random angles. A easy way would be just to hash the server number .
After placing the servers, the diagram would look like:

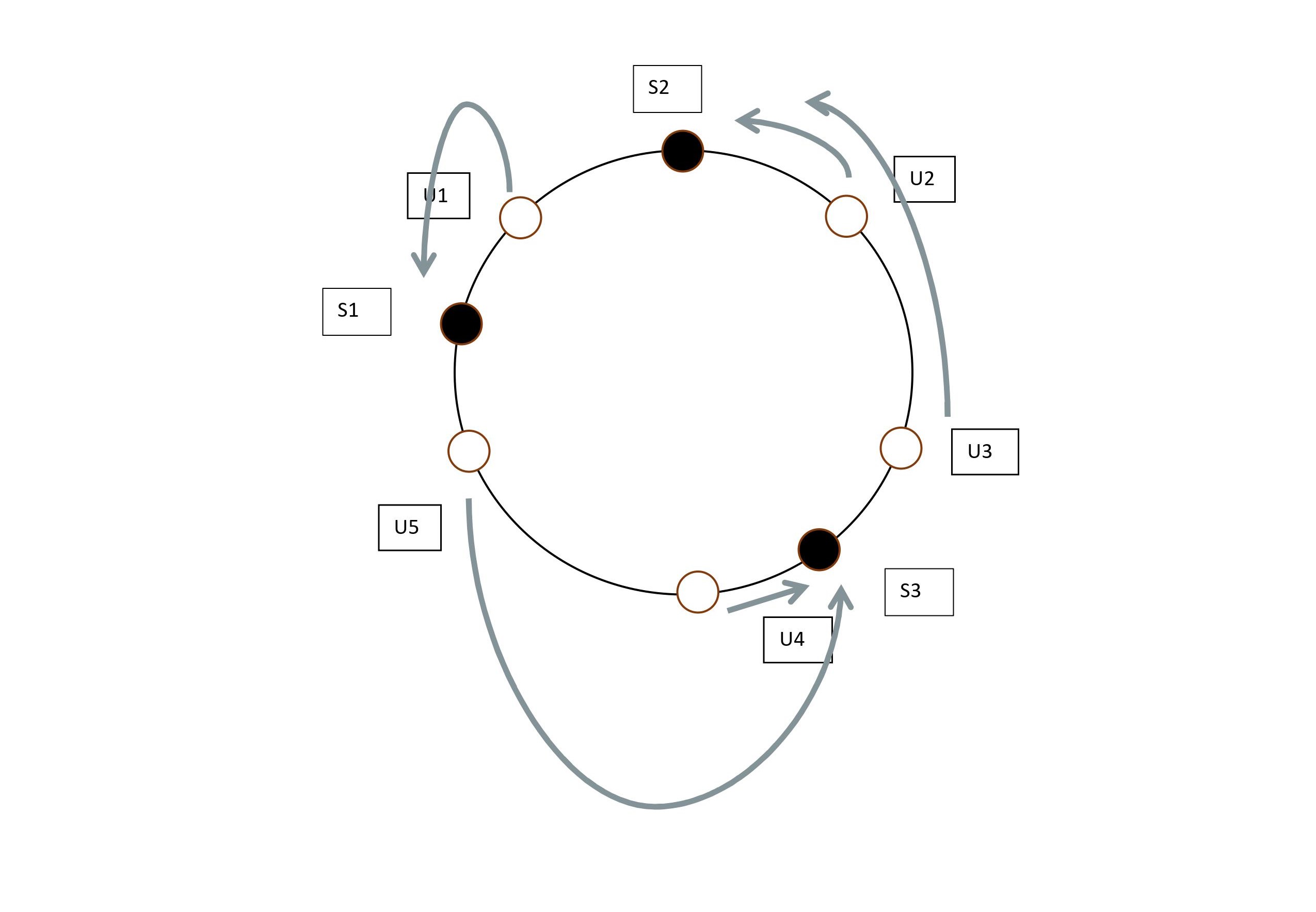
Now we've got both the users and the servers on the same diagram , we could map the users to the servers using association rule. Each user will belong to the closest server in the anti-clockwise direction (Clockwise could also be used). The Resultant figure would look like:

To Ensure that all users are distributed evenly among servers , we could use a simple trick like assigning more than one labels to each server.For example instead of using S1 , we could use S1₁ , S1₂ ,S1₃.S1 , S2 , S3 are replaced by these labels. The weight of each server is the factor by which we need to increase the number of labels. In our example we consider the weight of all servers to be equal. If say S3 was twice as powerful as S2 and S1 , then we would add twice as many labels for S3 when compared to labels added for S1 and S2. After replacing the servers with these labels , we get

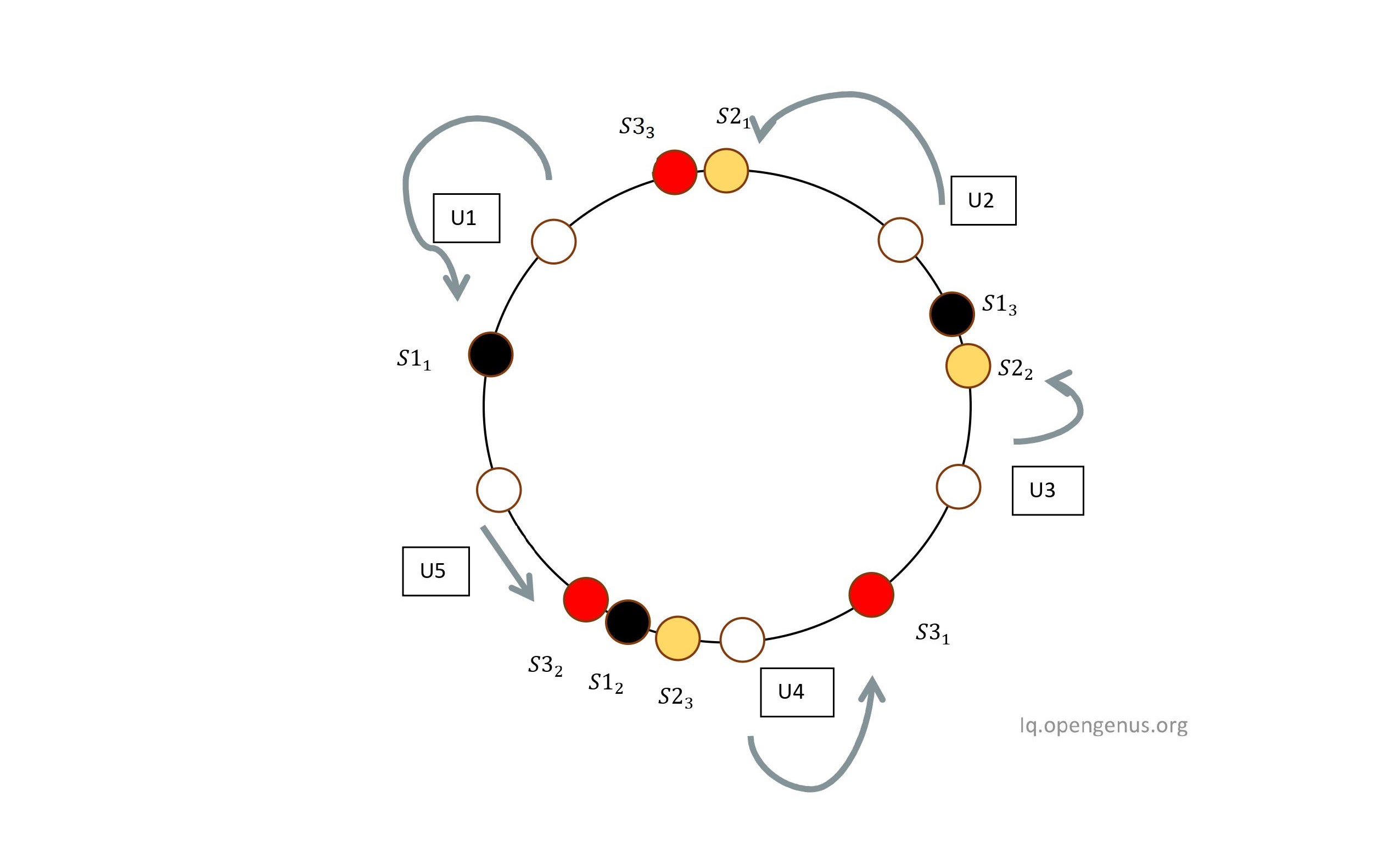
So you might ask , why bother adding so many labels , what's do we gain adding these labels? Well yes , we do. Remember that when we used servers directly without these labels , if we removed or added a server , all the users had to be remapped , but using this multiple labels trick helps us avoid remapping. Let's remove Server S1 with all its labels. What happens to users assigned to S1 , and are the others remapped? The users assigned to the S1 are assigned to the nearest server to them in counterclockwise direction. As U1 belonged to S1, after complete removal of S1 , going from counterclockwise direction from U1 yields S3₂ as it's nearest server , thus the user U1 is assigned to S3.

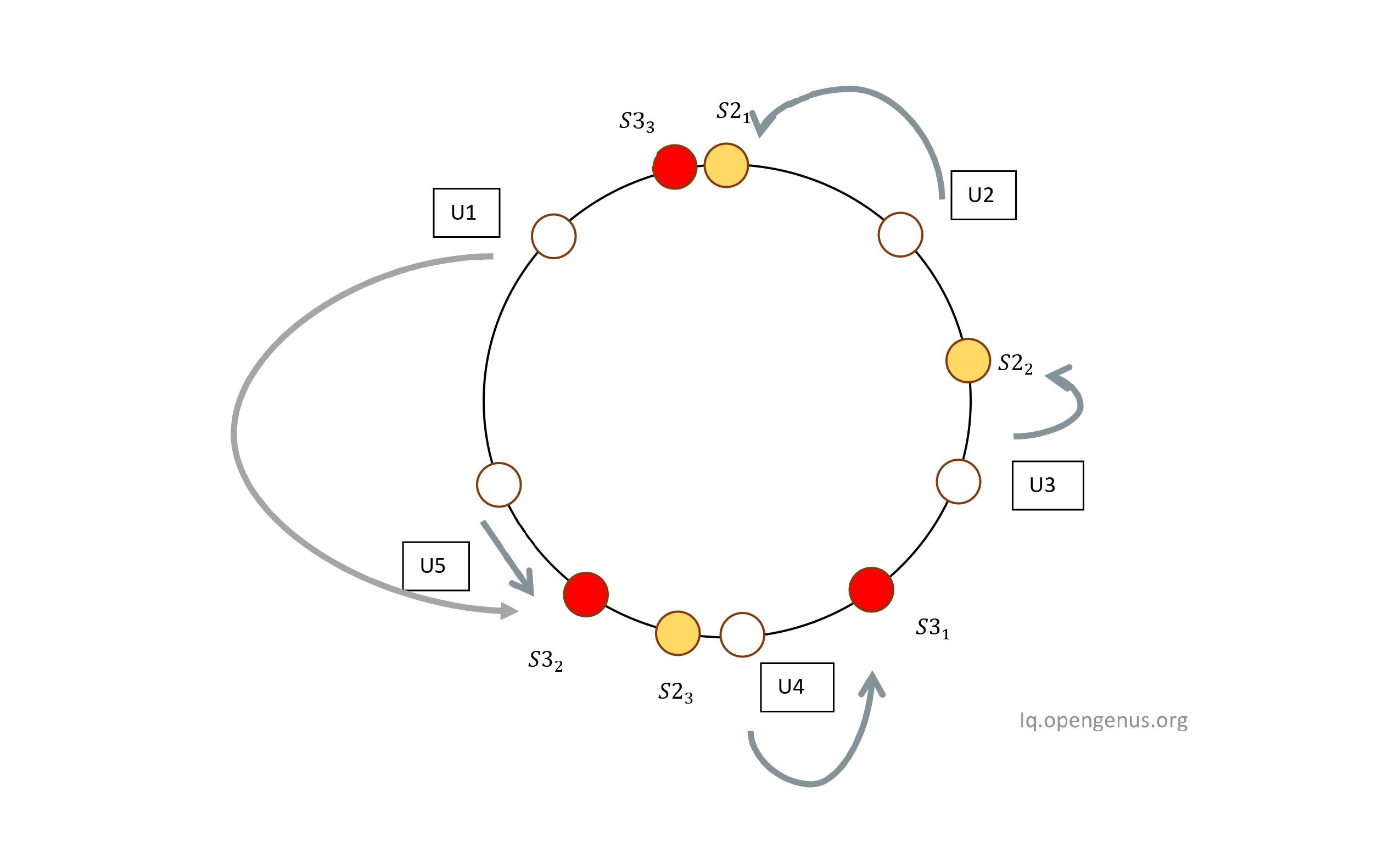
From the above diagram we can clearly see that U1 has now been assigned to another server but the real magic of consistent hashing is that the other users were untouched.

What if we wanted to add another server? Well the same benefit carries over but roughly a third of the users would be reassigned , and the rest would be untouched.

Generally, when we have N servers and K users(keys) , only K/N users(keys) would need to be remapped.