Pick’s Theorem in Computational Geometry

In this post, we dicuss Pick's theorem, its proof and example use cases where its application would be efficient to solve a problem. Using Pick's Theorem, we can compute the area of simple polygons.

Table of contents:

1. Pick's Theorem
2. Example 1
3. Example 2
4. Example 3: Proof for rectangles
5. Some applications of pick's theorem

Pick's Theorem

Pick's theorem allows us to easily compute the area of simple polygons (a polygon without holes) whose vertices are on points of an evenly spaced grid.

To compute area of such a polygon we need to know the number of interior points(points of the grid that are inside the polygon) and the number of boundary points(points of the grid that lie exactly on the boundary of the polygon).

To prove this theorem we show an additive factor whereby to come up with a proof for a polygon A, we use proofs from polygons b and c of which pick's theorem works.
That is, if we prove that picks theorem works for a 3-sided lattice polygon, then it can work for a 4-sided polygon and if it works for a 4-sided polygon, it works for a 5-sided polygon and et cetera.

Before we get to the proofs we first check to see if such a result can exist if the only things we have to take into account to calculate area of a polygon are its interior points and its boundary points

We will start by proving that three polygons with same number of interior points and boundary points have the same area.

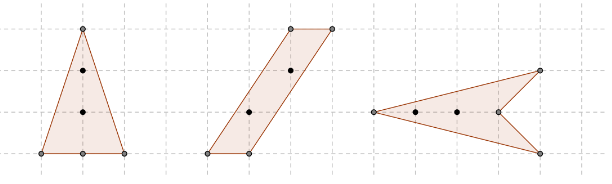
The above polygons have an 2 interior points and 4 boundary points an all have an area of 3.

Now we try to find that formula to compute this based solely on boundary points and interior points.

Let A denote area, B denote boundary points, I denote interior points.

We want to find a formula that looks like this
A = some dependant of B and I
$A=a\mathcal{I}+b\mathcal{B}+c$, we want to find a, b and c.

We use the the following polygons below to create sample data which we shall use to derive a formula.

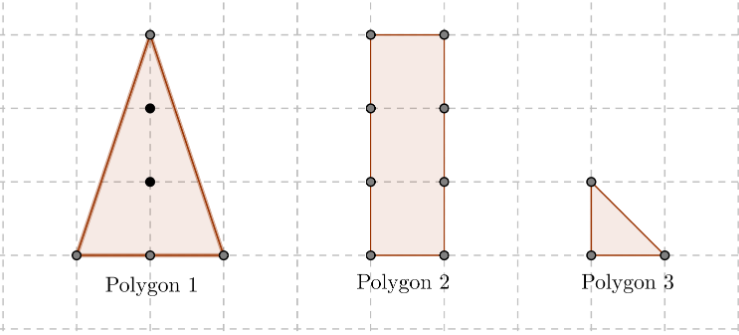
Data collected is the following

	polygon1	polygon2	polygon3
I	2	0	0
B	4	8	3
A	3	3	1/2

We plug the numbers into the formula $A=a\mathcal{I}+b\mathcal{B}+c$ and we have the following 3 equations.

3 = 2a + 4b + c
3 = 8b + c
$\frac{1}{2}$ = 3b + c

Solving the last two equation yields b = $\frac{1}{2}$c = -1 and when we replace b and c in equation 1 we get a = 1.

Therefore we have the following general equation a = I + $\frac{\mathcal{B}}{2}$ - 1.

Pick's theorem: The area of every simple polygon whose vertices lie line on the points of a grid is
$A=\mathcal{I}+\frac{\mathcal{B}}{2}-1$.

Example 1

Given the polygon below

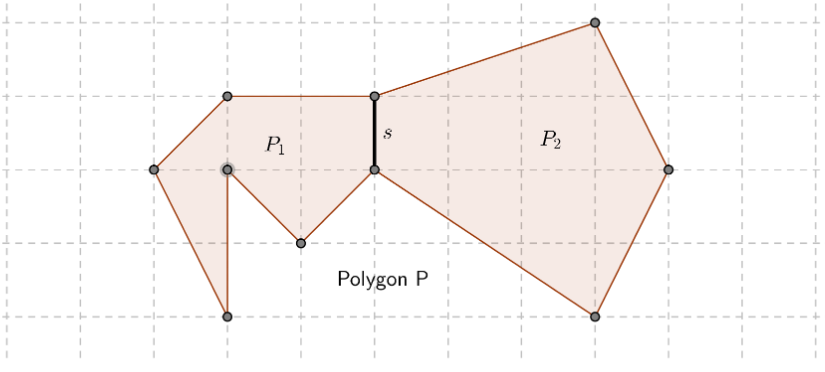
Let P1 and P2 be two polygons joined by a common side S, and P be the big polygon.
We denote picks theorem by $F=\mathcal{I}+\frac{\mathcal{B}}{2}-1$
We prove want to prove that $F_p=F_{p1}+F_{p2}$

Proof 1.

The interiors of polygon P are the union of the interior points of P1, the interior points of P2 and points of the grid that lie in the interior of the common side s.
That is $I_p=I_{p1}+I_{p2}+I_s$

Boundary points
If we sum up $B_{p1}$ and $B_{p2}$, we would have counted the boundary points of S twice whereas we need to count them once and we will also have counted the interior points twice whereas we need not include them at all since they are not a boundary.
Therfore we shall subtract interior points and boundaries that we have counted twice.
We have the following equation $B_p=B_{p1}+B_{p2}-2I_s-2$

Combining the two formulas we get the following,

$F_p=(I_{p1}+I_{p2}+I_s)+\frac{1}{2}(B_{p1}+B_{p2}-2I_s-2)-1$
$= (I_{p1}+\frac{1}{2}{B}_{p1}-1)+(I_{p2}+\frac{1}{2}{B}_{p2}-1) =$
$= F_{p1}+F_{p2}$

Example 2

Suppose picks theorem holds for P1 and P2 joined by S in example 1,
$A_{p1}=F_{p1}$ and $A_{p2}=F_{p2}$.

We prove that picks theorem also holds for the polygon P that is $A_p=F_p$.
The area of P is the sum of the areas of P1 and P2 that is $A_p=A_{p1}+A_{p2}$ and by proof 1 $F_p=F_{p1}+F_{p2}$.
That is, $A_{p1}=F_{p1}$ and $A_{p2}=F_{p2}$ therefore $A_p=F_p$.

We have shown that given a polygon we can join common polygons using common sides to construct the whole, that is combining the areas from two interior polygons of a whole will give the area of the whole.

We state that every polygon can be decomposed into triangles.
By this statement we have to come up with a proof for pick's theorem for triangles after which it goes to show that pick's theorem is true all polygons.

To come up with a proof of pick's theorem for triangles we are going to use the proof from rectangles with horizontal and vertical sides.

Example 3: Proof for rectangles

We prove that picks theorem is true for rectangles with vertical and horizontal sides.

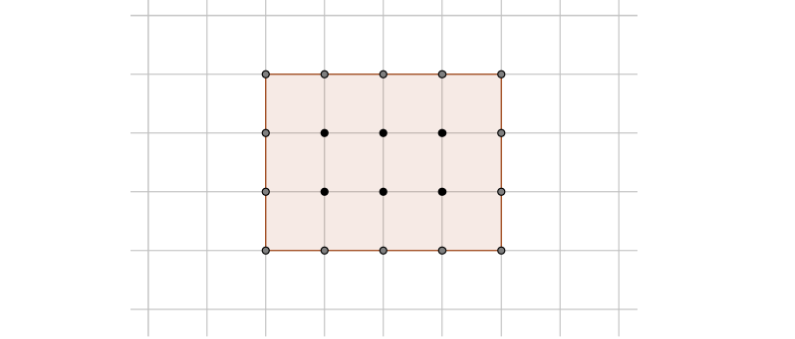
Proof 3.

Let R be the rectangle.
We can see the rectangle as a union of squares of side of 1.
From the result of example 2, we just have to prove the theorem for the smaller squares formed by the grid.
The squares have an area of 1, 4 boundary points and no interior points hence we have the following,

1 = 0 + $\frac{4}{2}$ - 1

We will use the proof from this example to prove picks theorem for triangles.

We classify triangles into 3 groups.

1. Right angle triangles with horizontal and vertical side.

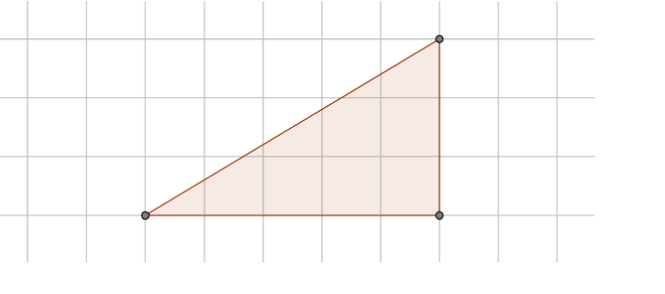
We inscribe the triangle in a rectangle

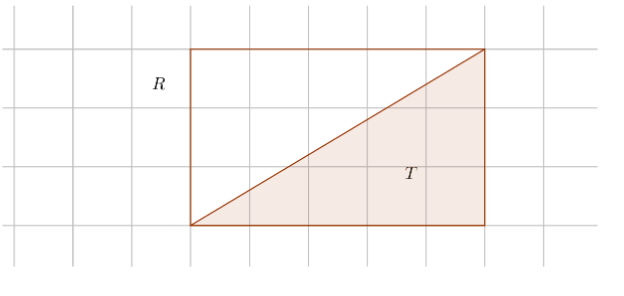
Proof 4.

We see that rectangle R is a union of triangle T and and another triangle like T. And by using proof 1 we have, $F_R=2F_T$.

The area of R is twice the area of T $A_R=2{\mathrm{A}}_T$

By proof 3, picks theorem holds true for R that is, $A_R=F_R$

By substituting $A_R$ and $F_R$ and dividing by 2 we have $A_T=F_T$
and with that we have proved that it holds true for triangle T.

2. Triangles with one horizontal or vertical side.

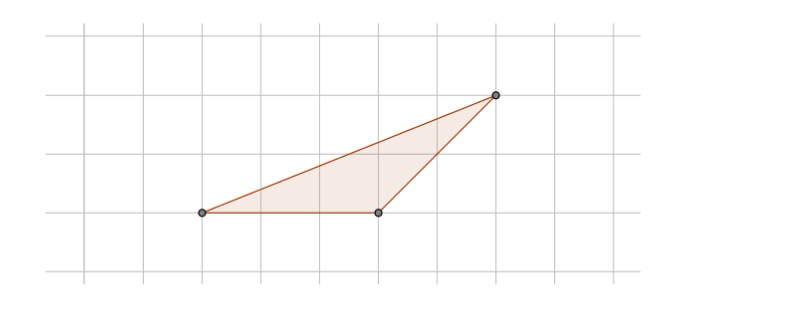
We inscribe the triangle in a rectangle

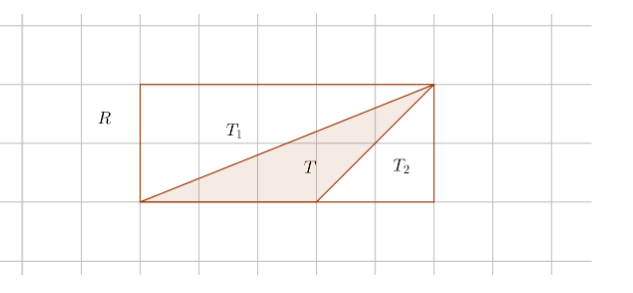
Proof 5.

We see rectangle R is a union of triangles T, T1, and T2 where T1 and T2 are triangles of type 1 which we have proved in 1 above.
Using proof 1, $F_R=F_T+F_{T1}+F_{T2}$

By proof 4 $A_{T\mathit{1}}=F_{T\mathit{1}}$

By proof 3 $A_R=F_R$

By combining the four four inequalities we have $A_T=F_T$

Therefore picks theorem holds for the triangle T.

3. Triangles without any vertical and horizontal sides.

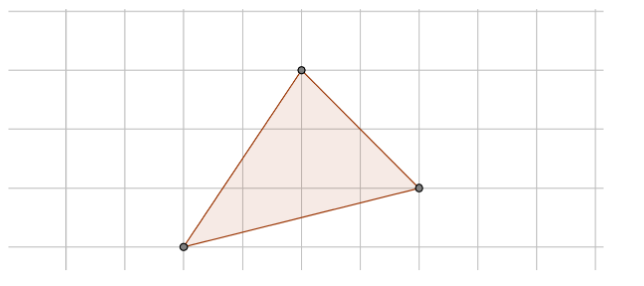
We inscribe the triangle in a rectangle

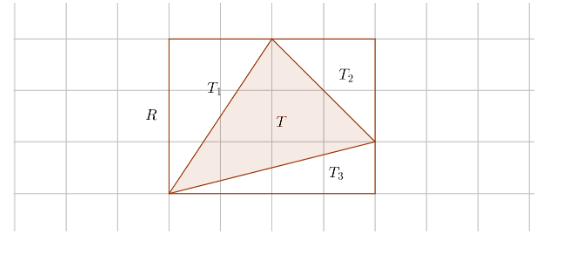
Another example,

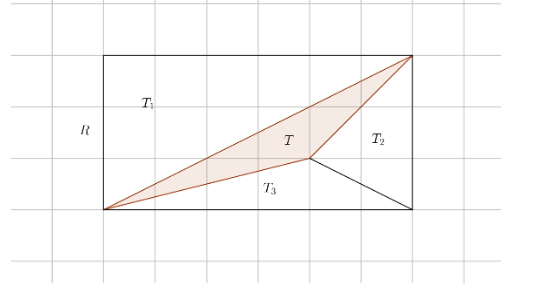
In the above diagram we see that only two vertices lie in the boundary of R.

Proof 6.

We see that rectangle R is a union of triangles T, T1, T2 and T3 where T1, T2 and T3 are triangles of type 1 or 2 as discussed in the two above cases.

In proof 3, 4 and 5 we have proved the theorem holds for R, that is T1, T2 and T3 respectively, with the same argument from proof 4 and 5, we find picks theorem must hold true for T too.

With that we are done, we have proved the lemma for triangles and said that we can decompose any polygon to triangles and proved pick's theorem for triangles.

Some applications of pick's theorem

1. We can use pick's theorem to determine area of a polygonal portion of a map, by counting the number of nodes inside the map and boundaries of the map region. We use pick's formula with a selected scale to come up with the area.
2. We want to plant trees in rows and columns on an island to form a rectangular grid, however the island is not rectangular. Using picks theorem we can find a polygon area with vertices lying on the grid points and plant the trees strictly inside this polygon.