Many applications of ConvNets require higher accuracy, and higher accuracy requires more parameters to learn and bigger networks, while the current SOTA (State of the art) Convnet have hit the memory limit it is time to look for more efficient ways to improve the accuracy. For that, we introduce in this article the EfficientNet model that suggests an efficient way for improving the performance of Convnets.

Table of content

1. Scaling a Convnet
2. Compound Scaling
3. EfficientNet architecture
4. EfficientNet performance
5. Conclusion

1. Scaling a Convnet

The process of scaling a Convnet is not yet well understood and there are many ways to do it. Based on the most common ways, it can be defined as adjusting the network's dimensions to achieve better performance. The dimensions of a Convnet are:

• Depth: it is the number of layers in the network. The deeper the network, the more likely it is to be more performant.
• Width: It is the number of channels in a convolutional layer.The wider the network the more it tend to capture fine-grained features and the easier it is to train.
• Resolution: is the resolution of the input images (width x height). As stated in [1], bigger images tend to help with accuracy with the overhead of more FLOPS.

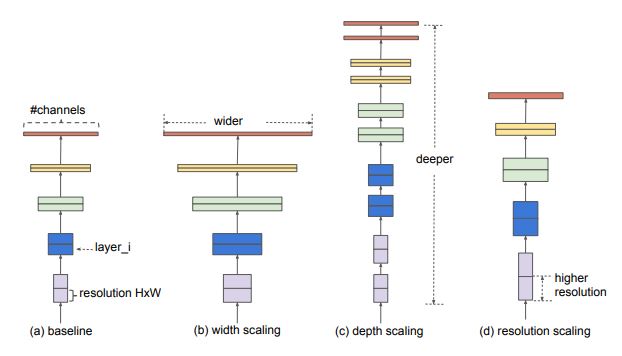
Usually, to scale a convnet, researchers tend to scale only one dimension. However, it is possible to arbitrary scale two or more dimensions, the only problem is that it requires tedious manual fine tuning and still often yields sub-optimal accuracy and efficiency. The authors of EfficientNet [1] showed that for a better scaling, it is necessary to balance all the dimensions of the network (width, depth and resolution) by uniformly scaling each one of them using a constant ratio, this method is called compound scaling.

2. Compound scaling

Instead of the regular method of trying to find the best layer architecture to get a better accuracy, the authors of EfficientNet suggest to start with a baseline network (N) and try to expand the length of the network (L), the width of the network (C) and the resolution (W,H) without changing the baseline architecture. Thus, the optimization problem can be defined as : finding the best coefficients for width (w),depth (d) and resolution(r) that maximizes the accuracy of the network under the constraints of the available resources (memory and number of possible operations (FLOPS)).

In order to further reduce the search space <L,C,W,H>, the authors also suggested to restrict that all layers must be scaled uniformly using a constant ratio. Thus, the dimensions of the network are defined as:

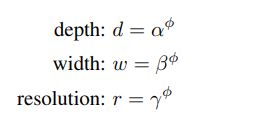
Where Φ is called the compound coefficient and α,β and γ are constants that can be found by a small grid search.

Φ is a coefficient specified by the user to control the amount of available resources. While α,β and γ assign these resources to the network's depth, width and resolution respectively.

It is also important to mention that the authors noticed that the FLOPS of a regular convolution operation are proportional to d, w², r². Since convolution operations dominate the computation cost in Convnets, using compound scaling on a Convnet increases the number of FLOPS by (α.β².γ²)^Φ, thus the constraint α.β².γ²≈2, to increase the total FLOPS by 2^Φ.

3. EfficientNet architecture

As mentioned earlier compound scaling does not change the operations used inside a layer of the network, instead it expands the network's width, depth and resolution. Hence, it is critical to have a good baseline network. The authors designed a mobile-size baseline network called EfficientNet-B0, that works by using a multi-objective neural architecture that optimizes accuracy and FLOPS. The model was inspired by Mnas-Net and has the following architecture.

EfficientNet-B0 architecture [2]

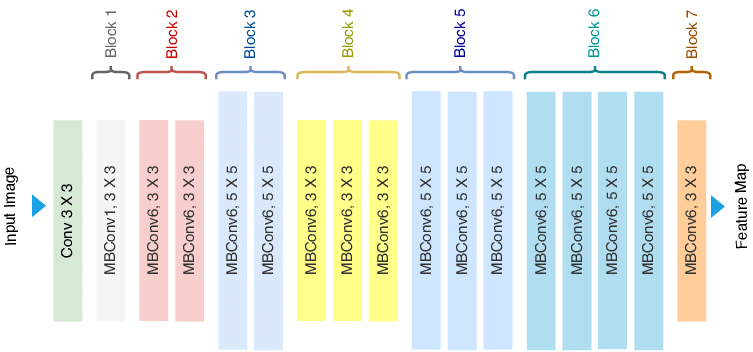
The building block of this architecture is the mobile inverted bottleneck MBConv that is also called inverted residual block with an additional SE (Squeeze and Excitation) block. These two blocks are explained bellow.

From the baseline network EfficientNet-B0, the authors applied the compound scaling method. First, they set Φ=1 and did a grid search to find the parameters α,β and γ based on the equations given in the previous section and under the constraint α.β².γ²≈2. The results were as follow α=1.2 , β=1.1 and γ=1.15.
In the next step, the founded parmeters were fixed, and the network's dimension equation was used to obtain a family of neural networks EfficientNet-B1 to B7 that they called EfficientNet.

MBConv

In order to make the information flows in deep neural networks, we usually use residual blocks. Residual blocks connect the beginning and the ending of a convolutional block with skip connections. The channels start being wide in the beginning of the convolutional block, then they get narrower along the depth of the block till the end where they become wide again because of the added information. Thus the pattern for a normal residual block in terms of channels number is wide->narrow->wide.

Structure of a normal residual block [3]

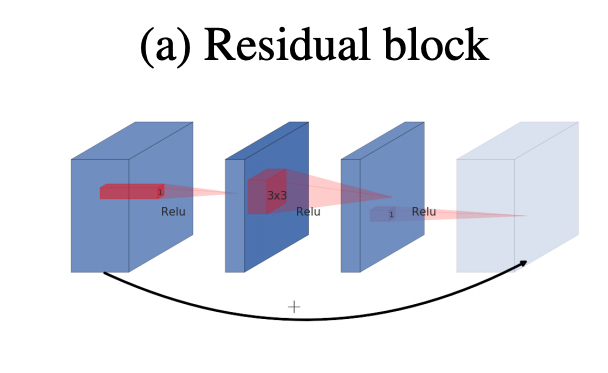
However, inverted residual block follows the inverse pattern of normal residual blocks, it means narrow->wide->narrow.

Structure of an inverted residual block (MBconv) [3]

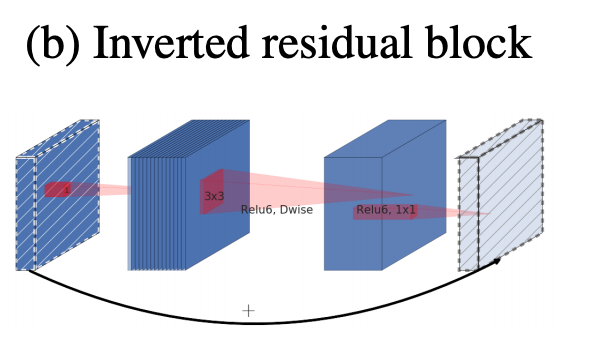
To understand the intuition behind it, we must mention that the aim of an MBConv is to make CNNs more efficient and adaptable for small platforms like mobiles. To do so, MBConv uses Depth-wise Separable Convolution [4]. First, the channels will be widened by a point-wise convolution (conv 1x1) then uses a 3x3 depth-wise convolution that reduces significantly the number of parameters and finaly it use a 1x1 convolution to reduce the number of channels so the beginning and the end of the block can be added. It is important to mention that before the addition operation, we apply a linear function to prevent non-linearities to destroy too much information as mentioned by the authors of MobileNetv2.

Squeeze and Excitation (SE) Block

SE is a building block for CNNs to improve the interdependencies between the channels by performing dynamic feature channel-wise recalibration, this means that instead of equally weighting all the channels, the network will dynamically assign high weight for the most important channels. The figure bellow shows the components of this block.

Architecture of an SE block.

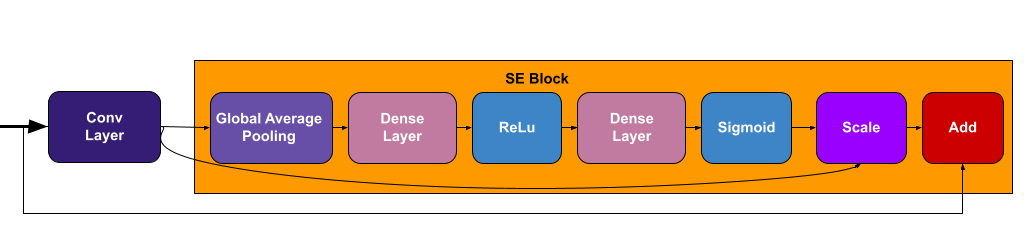
For a better understanding of this block, I highly suggest reading this article that explains it very well.

Coming back to our topic, EfficientNet applies the SE block along the way with the MBConv block which results in the following structure.

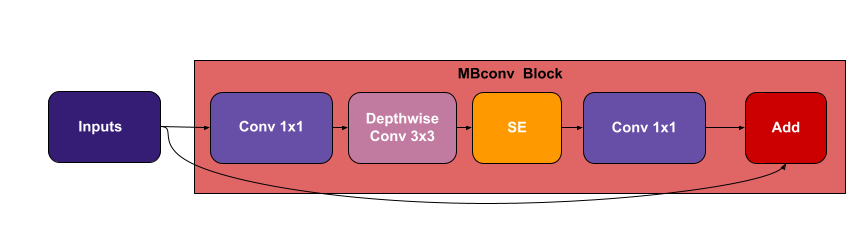
4. EfficientNet Performance

In order to evaluate the performance and the efficiency of EfficientNet, many benchmarks have been used. First, EfficientNet-B0 was scaled using different scaling methods.

Scaling up EfficientNet-B0 with different methods [1].

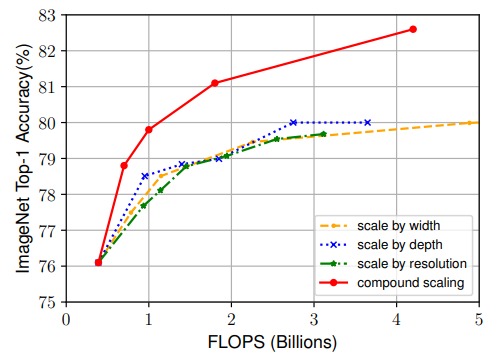
The compound scaling method outperformed the other methods as shown in the figure. Then the EfficientNet family has been tested on ImageNet dataset and it outperformed state of the art models in terms of efficiency and accuracy.

Comparison of EfficientNet family and other state of the art models on ImageNet dataset. (FLOPS vs Top accuracy) [1].

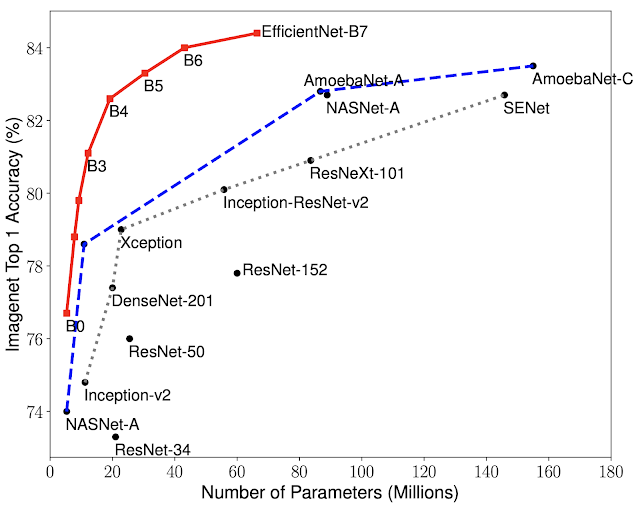
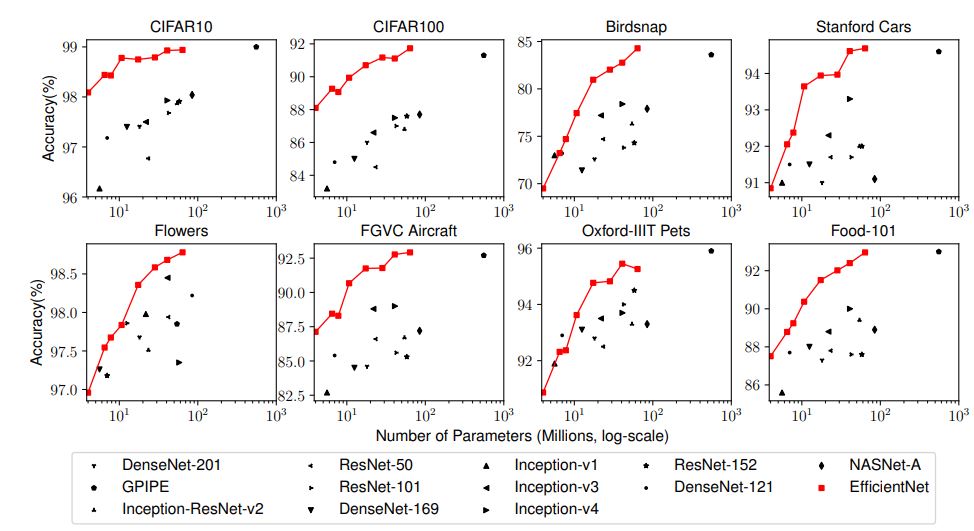
Finally, to further test the method's performance, the authors also performed benchmarks on transfer learning datasets, and the results also showed that EfficientNet transfer well.

Model parameters vs Transfer Learning Accuracy. (all models was trained on ImageNet and fine tuned on new datasets) [1].

5. Conclusion

As a wrap up, EfficientNet is a CNN that uses a scaling method called compound scaling that aims to improve the efficiency of an existing ConvNet based on the available resources (memory and FLOPS). The resulted networks proved to be both more efficient and more performant than many state of the art networks. Finally, the authors believe that the model can serve as new foundation for new computer vision models which is why they open sourced the TPU training code that can be found here.

References

[1] TAN, Mingxing et LE, Quoc. Efficientnet: Rethinking model scaling for convolutional neural networks. In : International conference on machine learning. PMLR, 2019. p. 6105-6114.
[2] Classification and understanding of cloud structures via satellite images with EfficientUNet - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Architecture-of-EfficientNet-B0-with-MBConv-as-Basic-building-blocks_fig4_344410350
[3] SANDLER, Mark, HOWARD, Andrew, ZHU, Menglong, et al. Mobilenetv2: Inverted residuals and linear bottlenecks. In : Proceedings of the IEEE conference on computer vision and pattern recognition. 2018. p. 4510-4520.
[4] CHOLLET, François. Xception: Deep learning with depthwise separable convolutions. In : Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. p. 1251-1258.