How many labeled and unlabeled binary tree can be there with N nodes?

In this article, we see how many labeled and unlabeled binary trees we can have with N nodes. This is related to the Catalan Numbers.

Binary Tree : A tree whose elements have 0 or 1 or 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

A Binary Tree node contains following parts:

1. Data
2. Pointer to left child
3. Pointer to right child

Labeled Binary tree - A Binary Tree is labeled if every node is assigned a label
Example:

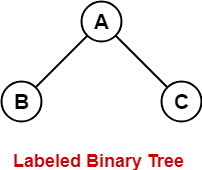
Unlabeled Binary Tree - A Binary Tree is unlabeled if nodes are not assigned any label.
Example:

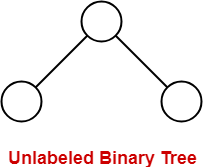
Unlabeled Binary tree

We have to count the total number of trees we can have with n nodes.
So for n=1 , Tree = 1
n=2 , Tree = 2
n=3, Tree = 5
n=4 , Tree = 14

Actually what we are doing is considering all possible pair of counts for nodes in left and right subtrees and multiplying the counts for a particular pair and then adding the results of all pairs.
But if we observe the pattern resembles the Catalan Numbers. The nth Catalan Number is given by:

T(n) = (2 n ) ! / [(n+1) ! n !]

Labelled Binary Tree

Here we can use the count of the unlabeled trees. Every unlabeled tree with n nodes can create n! labeled trees by assigning different permutations of labels to all nodes.

T(n) = [ (2 n ) ! / (n+1) ! n ! ] * n !