Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Given an array of N elements, our task is to find the least frequent element present in it. There are many ways to do this. In this article, we are going to talk about 3 of those methods along with their implementation.

Table of Contents

Different ways to find the least frequent element in an array
Naive Algorithm
Optimized algorithm with array sorting
Optimized algorithm with mapping

Different ways to find the least frequent element

We are going to be exploring three methods through which we will be able to find the least frequent element in an array and then print it. If there are multiple elements that appear the least number of times in the array, then we can print any one of them.

The three methods are:

Naive algorithm
Optimized algorithm with array sorting
Optimized algorithm with mapping

(1) Naive Algorithm

This is a very simple and straight-forward solution to this problem that doesn't really take the efficiency and complexity of the algorithm into account. It is a brute force algorithm.

The steps of Naive algorithm to find the least frequent element are as follows:

NOTE: Here arr is our main input array

Initialize the values of leastCtr and leastElement as the length of the input array and -99 respectively.
for i from 0 to length of arr do
2.1 Initialize the value of currentCtr as 0
2.2 for j from 0 to length of arr do
2.2.1 if (arr[i] == arr[j]) do
2.2.1.1 Increment the value of currentCtr by 1
2.3 if currentCtr < leastCtr do
2.3.1 Replace the values of leastCtr and leastElement with currentCtr and arr[i] respectively
By the time we reach this point, we will already have the least frequent element of the array stored in the leastElement variable and its count will be stored in the leastCtr variable.

Question

The time complexity of this algorithm should be:

O(n²)

O(logn)

O(n)

O(nlogn)

Correct! The time complexity of this algorithm is O(n²) as we have used nested loops here.

(a) Explanation

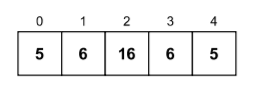
Let us consider the following array as our input.

naive algorithm

For each element of the outer loop i, the inner loop j checks if the element present at the ith index is equal to the element present at the jth index. If they are equal, then the currentCtr variable is incremented by 1.
When the control comes out of the inner loop, the algorithm then checks if the value of currentCtr is lesser than the value of leastCtr. If it is, then the value of leastCtr is replaced with the value of currentCtr.
The size of the given array is 5.
When i = 0 and the inner loop j has finished completely, the values of currentCtr, leastCtr, leastElement are updated to 2, 2 and 5 respectively because the value of currentCtr (2) was lesser than the value of leastCtr (5).
When i = 1 and the inner loop j has finished completely, the value of currentCtr is updated to 2. However, the value of leastCtr (2) and leastElement (5) remain the same as the value of currentCtr (2) is not less than leastCtr (2).
When i = 2 and the inner loop j has finished completely, the values of currentCtr, leastCtr, leastElement are updated to 1, 1 and 16 respectively because the value of currentCtr (1) was lesser than the value of leastCtr (2).
When i = 3 and the inner loop j has finished completely, the value of currentCtr is updated to 2. However, the value of leastCtr (1) and leastElement (16) remain the same as the value of currentCtr (2) is not less than leastCtr (1).
When i = 4 and the inner loop j has finished completely, the value of currentCtr is updated to 2. However, the value of leastCtr (1) and leastElement (16) remain the same as the value of currentCtr (2) is not less than leastCtr (1).
Finally, after the completion of the loops, the least frequent element in the array (leastElement) is found to be 16 and its count was found to be 1.

(b) Implementation in Python

Following is the implementation of our Naive approach in Python:

def findLeastFreqElementNaive(arr):
    leastCtr, leastElement = len(arr), -99
    for i in range(len(arr)):
        currentCtr = 0
        for j in range(len(arr)):
            if (arr[i] == arr[j]):
                currentCtr += 1
        if (currentCtr < leastCtr):
            leastCtr, leastElement = currentCtr, arr[i]
    return leastElement, leastCtr
    
if __name__ == "__main__":
    arr = [5, 6, 16, 6, 5]
    leastFreqElementNaive, ctr1 = findLeastFreqElementNaive(arr)
    print("====NAIVE ALGORITHM====")
    print("Given array:", arr)
    print("The least frequent element in the array is:", leastFreqElementNaive)
    print("Count of", leastFreqElementNaive,":", ctr1)

====NAIVE ALGORITHM====
Given array: [5, 6, 16, 6, 5]
The least frequent element in the array is: 16
Count of 16 : 1

(d) Complexity
Time complexity: O(N²)
Space complexity: O(1)

(2) Optimized algorithm with array sorting

This is an optimized algorithm which is much more efficient than the naive algorithm in terms of computational complexity. Firstly, we sort the array and then traverse through each element linearly while keeping a track of the frequency of the elements.

The steps of our optimized algorithm using sorting to find the least frequent element are as follows:

NOTE: Here arr is our main input array

Copy the contents of the input array to a new variable temp_arr. The motivation behind this step is so that the original order of the input array is maintained and we can perform the required operations on the temporary array.
Initialize the values of leastCtr, leastElement and currentCtr as the length of the input array, -99 and 1 respectively.
Perform the sorting operation on temp_arr. For example, it will be temp_arr.sort() on Python.
for i from 0 to (length of temp_arr) - 1 do
4.1 if temp_arr[i] == temp_arr[i + 1] do
4.1.1 Increment the value of currentCtr by 1
4.2 else do
4.2.1 if currentCtr < leastCtr do
4.2.1.1 Replace the values of leastCtr and leastElement with currentCtr and temp_arr[i] respectively
4.2.2 Reset the value of currentCtr to 1
if currentCtr < leastCtr do
5.1 Replace the values of leastCtr and leastElement with currentCtr and temp_arr[len(temp_arr) - 1] respectively. We are performing this extra check because this check would not be performed for the last element in the array in our main loop. This is why we have to explicitly check if the last element in the input array is the least frequent element in the array or not.
By the time we reach this point, we will already have the least frequent element of the array stored in the leastElement variable and its count will be stored in the leastCtr variable.

Question

The time complexity of this algorithm should be:

O(n)

O(n + nlogn)

O(n²)

O(nlogn)

Correct! The time complexity of this algorithm is O(nlogn).

(a) Explanation

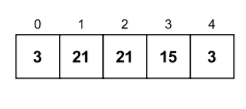
Let us consider the following array as our input.

sortExplanation1

Firstly, the array is sorted.
After sorting, for each i from 0 to the size of the array minus 1, i.e., 4, we check if the value of temp_arr[i] is equal to the value of temp_arr[i + 1]. If it is, then we increment the value of currentCtr and go back to the loop.
However, if the value of temp_arr[i] is not equal to the value of temp_arr[i + 1], then we check if the value of currentCtr is lesser than the value of leastCtr. If it is, then we update the values of leastCtr and leastElement to currentCtr and temp_arr[i] respectively.
When i = 0, the values of leastCtr and leastElement remain 5 and -99 respectively. Since the value of temp_arr[i] (3) is equal to the value of temp_arr[i + 1] (3), the value of currentCtr is incremented by 1 (becomes 2) and then the control goes back to the start of the loop.
When i = 1, the value of temp_arr[i] (3) is not equal to the value of temp_arr[i + 1] (15), and the value of currentCtr is lesser than the value of leastCtr, therefore the values of leastCtr is set to the value of currentCtr (2) and the value of leastElement becomes temp_arr[i] (3). After that, the value of currentCtr is reset to 1 and the control goes back to the start of the loop.
When i = 2, since the value of temp_arr[i] (15) is not equal to the value of temp_arr[i + 1] (21), the values of leastCtr (2) and leastElement (3) are set to 1 and 15 respectively. The control then goes back to the main loop.
When i = 3, the value of temp_arr[i] (21) is equal to the value of temp_arr[i + 1]. The value of currentCtr (1) is incremented and becomes 2 and then the loop finally stops.
One final check is performed to check if the last element is the least frequent element in the array. However, that is not the case in our input array, so we simply return the values of leastElement (15) and leastCtr (1).

(b) Implementation in Python

Following is the implementation of our Optimized algorithm with array sorting in Python:

def findLeastFreqElementSorting(arr):
    temp_arr, leastCtr, leastElement, currentCtr = arr.copy(), len(arr), -99, 1
    temp_arr.sort()
    for i in range(len(temp_arr) - 1):
        if (temp_arr[i] == temp_arr[i + 1]):
            currentCtr += 1
        else:
            if (currentCtr < leastCtr):
                leastCtr, leastElement = currentCtr, temp_arr[i]
            currentCtr = 1
    if (currentCtr < leastCtr):
        leastCtr, leastElement = currentCtr, temp_arr[len(temp_arr) - 1]
    return leastElement, leastCtr
    
if __name__ == "__main__":
    arr = [3, 21, 21, 15, 3]
    leastFreqElementSorting, ctr2 = findLeastFreqElementSorting(arr)
    print("====OPTIMIZED ALGORITHM WITH SORTING====")
    print("Given array:", arr)
    print("The least frequent element in the array is:", leastFreqElementSorting)
    print("Count of", leastFreqElementSorting,":", ctr2)

(c) Output

====OPTIMIZED ALGORITHM WITH SORTING====
Given array: [3, 21, 21, 15, 3]
The least frequent element in the array is: 15
Count of 15 : 1

(d) Complexity

Time complexity: O(N logN)
Space complexity: O(N) (because of the usage of the sort() method)

(3) Optimized algorithm with hash mapping

This is another optimized algorithm which is much more efficient than the naive algorithm in terms of computational complexity. Since we are using the python language, we will make use of the dictionary data structure to implement this algorithm with mapping.

The algorithm is illustrated below:-

NOTE: Here arr is our main input array
1. Declare dictMap as an empty dictionary. We will map the elements and their frequencies here.
2. for i from 0 to length of arr do
2.1 if arr[i] is present in dictMap as a key do
2.1.1 Increment the value corresponding to the key arr[i] by 1 in dictMap
2.2 else do
2.2.1 In dictMap, initialize the key arr[i] with its value as 1
3. Put the least value present in dictMap in the leastElementCtr variable. For example, in python, it can be simply done by calling the min method as min(dictMap.values())
4. for every key i in dictMap do
4.1 if dictMap[i] == leastElementCtr do
4.1.1 Initialize the value of the variable leastElement as i
4.1.2 break the loop
5. By the time we reach this point, we will already have the least frequent element of the array stored in the leastElement variable and its count will be stored in the leastCtr variable.

Question

The time complexity of this algorithm should be:

O(n)

O(n + k)

O(n²)

O(nlogn)

Correct! The time complexity of this algorithm is O(n).

(a) Explanation

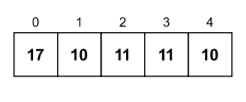
Let us consider the following array as our input.
mapExplanation1-1

For each index i (0 to 4) in the array, if arr[i] is not present in our dictionary dictMap, we make an addition to dictMap with the key being arr[i] and the value being 1. If the the value arr[i] is present in our dictMap, then we simply increment the value by 1 that corresponds to the key dictMap[arr[i]].
After all the values (frequencies) have been mapped to their respective keys (elements), we then run a final loop to find the key (element) with the minimum value (frequency). After this loop, we can simply return the least frequent element and its frequency as well.
In the first loop, when i = 0, we insert the key-value pair of 17: 1 to dictMap.
dictMap = {17: 1}
When i = 1, we insert the key-value pair of 10: 1 to dictMap.
dictMap = {17: 1, 10: 1}
When i = 2, we insert the key-value pair of 11: 1 to dictMap.
dictMap = {17: 1, 10: 1, 11: 1}
When i = 3, since arr[i] (11) is present in dictMap, we increment the value by 1 in dictMap where the key is arr[i].
dictMap = {17: 1, 10: 1, 11: 2}
When i = 4, since arr[i] (10) is present in dictMap, we increment the value by 1 in dictMap where the key is arr[i].
dictMap = {17: 1, 10: 2, 11: 2}
The key (element) with the minimum frequency is found to be 17 with a frequency of 1. We can return these values now as the final result has been computed.

(b) Implementation

Implementation of our Optimized algorithm with hash mapping in Python:

def findLeastFreqElementMapping(arr):
    dictMap = {}
    for i in range(len(arr)):
        if (arr[i] in dictMap.keys()):
            dictMap[arr[i]] += 1
        else:
            dictMap[arr[i]] = 1
    leastElementCtr = min(dictMap.values())
    for i in dictMap:
        if dictMap[i] == leastElementCtr:
            leastElement = i
            break
    return leastElement, leastElementCtr
    
if __name__ == "__main__":
    arr = [17, 10, 11, 11, 10]
    leastFreqElementMapping, ctr3 = findLeastFreqElementMapping(arr)
    print("====OPTIMIZED ALGORITHM WITH MAPPING====")
    print("Given array:", arr)
    print("The least frequent element in the array is:", leastFreqElementMapping)
    print("Count of", leastFreqElementMapping,":", ctr3)

(c) Output

====OPTIMIZED ALGORITHM WITH MAPPING====
Given array: [17, 10, 11, 11, 10]
The least frequent element in the array is: 17
Count of 17 : 1

(d) Complexity

Time complexity: O(N)
Space complexity: O(1)

Summary

As a summary of our three methods for finding the least frequent element are:

Naive algorithm O(N^2) time, O(1) space.
Optimized algorithm with array sorting O(N logN) time, O(1) space.
Optimized algorithm with mapping O(N) time, O(N) space.

With this article at OpenGenus, you must have the complete idea of different efficient approaches to find the Least frequent element in an array.

Least frequent element in an array

Algorithms Sorting Algorithms hash map Interview Problems on Array

Different ways to find the least frequent element

(1) Naive Algorithm

Question

The time complexity of this algorithm should be:

(a) Explanation

(b) Implementation in Python

(2) Optimized algorithm with array sorting

Question

The time complexity of this algorithm should be:

(a) Explanation

(b) Implementation in Python

(c) Output

(d) Complexity

(3) Optimized algorithm with hash mapping

Question

The time complexity of this algorithm should be:

(a) Explanation

(b) Implementation

(c) Output

(d) Complexity

Summary

THANK YOU!

Number of palindromic substrings in a string

What Java Programmers Should Learn In 2021?