Local response normalization (LRN)

In this article, we have explained the concept of Local response normalization (LRN) in depth along with comparison with Batch Normalization.

Table of contents:

1. Introduction to Normalization
2. Local response normalization (LRN)
3. Local response normalization (LRN) in TensorFlow
4. Batch Normalization vs Local response normalization (LRN)

Pre-requisite:

• Normalization in Machine Learning: A Breakdown in detail
• Batch Normalization

Introduction to Normalization

Normalization is used in deep neural networks to compensate for the unbounded nature of activation functions like ReLU, ELU, and others. These activation functions' output layers are not limited to a finite range (like [-1,1] for tanh), but can rise as far as the training allows. To save you unbounded activation from elevating the output layer values, normalization is used simply earlier than the activation function.

Local response normalization (LRN)

Local Response Normalization (LRN) become first utilized in AlexNet architecture, with ReLU serving because the activation function rather than the more common tanh and sigmoid. In addition to the reasons described above, LRN was used to enhance lateral inhibition.

Local Response Normalization is a normalization layer that makes use of lateral inhibition to put in force the notion. Lateral inhibition is a neurobiological concept that outlines how stimulated neurons repress nearby neurons, intensifying the sensory experience and producing maximal form spikes that create contrast in the area. You can normalize within or between channels when using LRN to normalize a convolutional neural network.

The LRN primitive conducts forward and backward normalization of local responses.
Inter-Channel LRN:

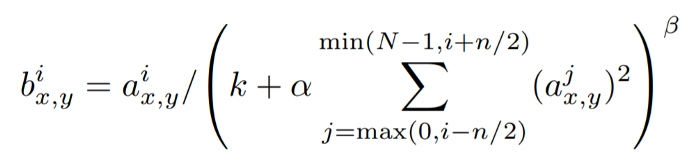
The pixel values at (x,y) location before and after normalization are i,a(x,y), and b(x,y), respectively, and N is the total number of channels. (k,α,β,n) are hyper-parameters that are constants. k is a normalization constant and a contrasting constant that is used to avoid any singularities (zero division). The n constant specifies the neighborhood length, or how many consecutive pixel values must be considered during normalization. (k,α,β,n) is the traditional normalization formula (0,1,1,N).

First, the activation is contained within the sum operator; we square it to cancel out the positive-negative effects. Let's look at what the range of the sum operator is. Given an n, it iterates n/2 to the left and n/2 to the right, while keeping the boundaries, 0 and N-1, in mind.This is then multiplied by a factor, to reduce its value in comparison to the numerator, in order to preserve the value of the activation in the numerator (if is too high, the activation in the numerator will be diminished, resulting in vanishing gradients; if is too low, exploding gradients will result). k is added to avoid a division by zero error.

Finally, β is used as an index to determine the effect of this local response on problem activation. The higher the beta value, the higher the penalty for adjacent activations, but the lower beta value has little effect on the activation in question.

Intra-channel LRN: Neighborhood is extended only within the same channel of intra-channel LRN. The formula is:

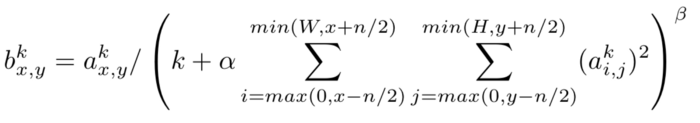
where (W,H) is the width and height of the feature map.

The neighborhood for normalization is the only variation between Inter and Intra Channel LRN.A 2D neighborhood is defined around the pixel under consideration in Intra-channel LRN (as opposed to a 1D neighborhood in Inter-Channel LRN).

Local response normalization (LRN) in TensorFlow

Tensorflow The implementation is as follows ：

import tensorflow as tf
import numpy as np
x = np.array([i for i in range(1, 33)]).reshape([2, 2, 2, 4])
y = tf.nn.lrn(input=x, depth_radius=2, bias=1, alpha=1, beta=0.75)
print("input:\n", x)
print("output:\n", y)


input:
 [[[[ 1  2  3  4]
   [ 5  6  7  8]]

  [[ 9 10 11 12]
   [13 14 15 16]]]


 [[[17 18 19 20]
   [21 22 23 24]]

  [[25 26 27 28]
   [29 30 31 32]]]]
output:
 tf.Tensor(
[[[[0.13119929 0.15223296 0.22834945 0.3120463 ]
   [0.14621021 0.1247018  0.14548543 0.18664722]]

  [[0.1239255  0.1028654  0.11315194 0.14340706]
   [0.10845583 0.08916934 0.09553858 0.12041976]]]


 [[[0.09743062 0.079716   0.08414467 0.10572015]
   [0.08913988 0.07271773 0.07602308 0.09531549]]

  [[0.08263378 0.06727669 0.06986426 0.08746313]
   [0.07735948 0.06289289 0.06498932 0.08126954]]]], shape=(2, 2, 2, 4), dtype=float32)

Batch Normalization vs Local response normalization (LRN)

Batch normalization is a supervised learning technique for transforming the middle layer output of neural networks into a common form. This effectively "reset" the distribution of the output of the previous layer, allowing it to be processed more efficiently in the next layer. This technique speeds up learning because normalization prevents activation values from being too high or too low and allows each layer to learn independently of the other layers.

Normalizing the input reduces the "dropout" rate or data loss between processing layers. This greatly improves the accuracy of the entire network..

To boom the steadiness of the deep learning network, batch normalization influences the output of the preceding activation layer via way of means of subtracting the batch normalization imply and dividing it via way of means of the batch standard deviation.

This shift or scaling of the output with randomly initialized parameters reduces the accuracy of the weights of the next layer, so if the loss function is too large, use stochastic gradient descent to do this normalization.

Batch normalization provides the layer with two more trainable parameters. The gamma (standard deviation) and beta (mean) parameters are multiplied by the normalized result. This allows stack normalization and gradient descent to work together to "denormalize" the data by simply changing two weights per output. By adjusting all other related weights, data loss was reduced and network stability was improved.

Batch normalization, on the other hand, can only be done in one way, but local response normalization has different directions for performing normalization between or within channels.

With this article at OpenGenus, you must have the complete idea of Local response normalization (LRN).