In this article, we will learn how to find the mirror image position of a point in a 2D plane along with C++ implementation of the approach.

Table of contents

1. Problem Statement
2. Mirror Equation
3. Implementation
4. Code

Problem Statement

Given a point P(x1,y1) in 2-D plane, find the image of the point P(x1,y1) formed due to the mirror.

Sample input :
(5,1)
Sample output :
Image -> (1,5)

Mirror Equation

In order to get mirror image we must have a mirror first.
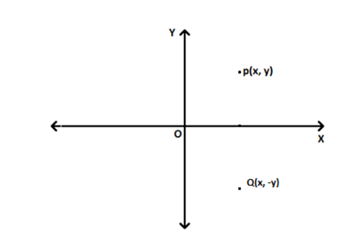
You can observe in this image that mirror image of point P(x,y) is Q(x,-y) when we take x-axis as mirror.
Mirror image is always equidistant from the mirror, in this case the distance from x-axis(mirror) to point P and distance from x-axis to point Q is same that is |y|.

Formula for line equation (mirror equation) -> ax+by+c=0
where x and y is the middle point of mirror image and actual point.

In this image we can observe that the mirror used here is y-axis and both the points are equidistant from the mirror.

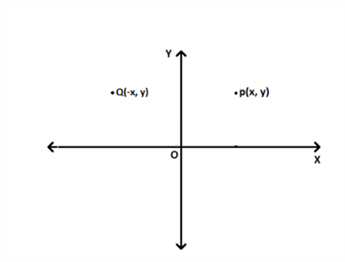
Now, for simplicity we will take our mirror in the first quadrant where x and y are both positive. Imagine a line from the origin at 45 degrees from both x-axis and y-axis.

For this line mirror equation will be -> (-1)x + (1)y + 0 = 0

Now, when we have a mirror equation, we can use this formula below to get mirror image of a actual point with respect to the mirror (-1)x +(1)y + 0 = 0

Formula to get mirror image :-

(x-x1)/a = (y-y1)/b = -2(ax1+by1+c)/(a²+b²)

Implementation

1. Make a function which applies the above formula and returns the value of x and y cordinate of mirror image in a pair of double integer (x,y).
2. Initialize coefficient of mirror equation.
3. Take input from user , the actual point (x1,y1)
4. Run the function and output the mirror image position.

->Note that we can use any line as mirror, but in this we will use this mirror equation because it is symmetric through both the axis.

Code :

   #include <iostream>
   using namespace std;
 

   pair<double, double> mirrorimage(double x1, double y1)
   {
    //coefficients of mirror equation
    double a = -1.0;
    double b = 1.0;
    double c = 0.0;
    
    //Formula used for mirror image 
    double temp = -2 * (a * x1 + b * y1 + c) / (a * a + b * b);
    
    //mirror image of (x1,y1)
    //kept x one side and sent a and -x1 to other side to get this equation , same for y.
    double x = temp * a + x1;
    double y = temp * b + y1;
    return make_pair(x, y);
   }
 
int main()
{
   double x1,y1;
   cout<<"Enter the point x1 : ";
   cin>>x1;
   cout<<"Enter the point y1 : ";
   cin>>y1;
   pair<double,double> image;
   image = mirrorimage(x1,y1);
   cout<<"Mirror image of ("<<x1<<","<<y1<<") is : ("<<image.first<<","<<image.second<<")";
 
    return 0;
}

Sample output

Enter the point x1 : 10
Enter the point y1 : 9 
Mirror image of (10,9) is : (9,10)

With this article at OpenGenus, you must have the complete idea of Finding mirror image of point in 2D plane.