Number of closed islands [2 solutions]

In this article, we have explored how to find the Number of closed islands in a graph. We have presented two approaches using the concept of BFS/ DFS and Union Find.

Pre-requisites:

• BFS and DFS
• Union Find

Problem Statement

Given a 2-D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example:

Output: 2

Explanation: Here the 0s which are marked inside the box are only considered to be closed islands as they are completely surrounded by 1s and follows the rest of the conditions

Observations

So from the question and the example we can say the following:

• we can't connect 0s or 1s diagonally in any case.
• connection can happen only in the four fundamental directions.
• the 0s in the border will never be an island as they are not covered by 1s from all sides.
• the 0s joining the 0s in the border can never be a part of a closed island.

Now lets solve it.

Approach 1

In this approach we will discuss a way to solve this problem using BFS/DFS. We will follow the following steps to solve it.

• We will start our iteration from grid[1][1] as we don't have to consider the border elements.
• Once we encounter a 0 we will first change it to another number lets say -1 to keep track of the visited grounds.
• Then we will change all 0s neighbors horizontally or vertically from the current ground using a recursive function.
• The recursive function will return true if that cell is visited or if its a 1
• If its a ground not visited then it will return false if its out of boundary.
• Then it would change the cells value to -1 as we have visited it and then call the recursive function in all four direction.
• Then it would return the && value of all directions.

Let's look at the code it understand it better.

#include <iostream>
#include <vector>

using namespace std;

bool isClosedIsland(vector<vector<int>> &grid, int i, int j, int r, int c)
{
    if (grid[i][j] == 1 || grid[i][j] == -1)
        return true;
    if (i <= 0 || i >= r - 1 || j <= 0 || j >= c - 1)
        return false;
    grid[i][j] = -1;

    bool top = isClosedIsland(grid, i - 1, j, r, c);    // Top
    bool bottom = isClosedIsland(grid, i + 1, j, r, c); // Bottom
    bool left = isClosedIsland(grid, i, j - 1, r, c);   // Left
    bool right = isClosedIsland(grid, i, j + 1, r, c);  // Right

    return top && bottom && left && right;
}

int closedIsland(vector<vector<int>> &grid)
{
    if (grid.size() == 0)
        return 0;
    int cnt = 0, r = grid.size(), c = grid[0].size();
    for (int i = 1; i < r - 1; i++)
    {
        for (int j = 1; j < c - 1; j++)
        {
            if (grid[i][j] == 0)
            {
                if (isClosedIsland(grid, i, j, r, c))
                {
                    cnt++;
                }
            }
        }
    }
    return cnt;
}

int main()
{
    int r, c;
    cin >> r >> c;
    vector<vector<int>> grid(r, vector<int>(c));
    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            cin >> grid[i][j];
        }
    }
    cout << closedIsland(grid) << endl;
    return 0;
}

The time and space complexity of the above approach will be O(r*c), where r is the number of rows and c is the number of columns in the matrix.

Approach 2

Here in this approach we will taking an insightful approach using union find.

First we would accept the vector and then numIslands() is called. Inside numsIsland first we will make all the lands or 0s in the border, and the ones having connection to those in horizontal and vertical direction of the grid will be converted to 1s or any other number as you wish. We will be doing this with changeCorner() and recursively calling change() inside it. The reason why we are doing this is in the observation section, ie, those elements will never be a part of a closed island. So the remaining zeros after this step will be a part of a closed island or itself be one.

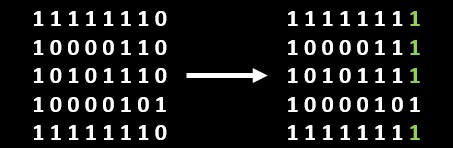
So after this we will initialize a vector of pairs edges, we will use this to store all the connections a particular ground or 0 have with adjacent cells in right and downward direction.
Now we will iterate through the grid again, this time when we encounter a 0 we will calculate a unique id for that cell using the formula i*n+j and will check if the cells in both direction are 0s or not, if its there then we will calculate an id for both of them and will push id, right_id and id, down_id into the vector. For the above grid the following will be the edges vector.

                                1 1 1 1 1 1 1 1               9  10
                                1 0 0 0 0 1 1 1               9  17
                                1 0 1 0 1 1 1 1    --->      10  11
                                1 0 0 0 0 1 0 1              11  12
                                1 1 1 1 1 1 1 1              11  19
                                                             17  25
                                                             19  27
                                                             25  26
                                                             26  27
                                                             27  28

Now we will form another vector of size r*c where r and c are the rows and columns of the grid. This vector would act as a hash vector, so we will call it a hashSet. We will initialize the value of hashSet with the values of i. Then we will iterate through the edges vector and use Union() for each of the pair. In Union() we will use find() for each element in the pair. The find() uses the passed value and the hashSet to find the root or starting of the island chain. If the value and the hashSet value are equal then it would return the same value else it uses the while() loop to find the starting of the chain. If the root value of both the edges are different then we change the values in the hashSet, this is done from the Union() itself, since they are adjacent and part of the same chain. By the end of this step the starting node id's index inside the hashSet will have same value as its index and the rest of them will have the index value of other nodes which would connect them with these starting nodes. The following is the hashSet value for the given grid.

0 1 2 3 4 5 6 7 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
0 1 2 3 4 5 6 7 8 10 17 12 19 13 14 15 16 11 18 25 20 21 22 23 24 27 28 26 28 29 30 31 32 33 34 35 36 37 38 39

Now we will count the elements, for this we will traverse through the grid again and for each 0 we encounter we will check if the hashSet[i]==i if it is that means that 0 is the starting point of the island chain and we will increment the value by one. Here we use an interesting technique to iterate through the grid and the hashSet at the same time. By the end of this step we will have the count of closed islands in the given grid.

Note: If you check carefully if one 0 is being surrounded by 1s in all sides then it was not considered in the hashSet, but in this step we will count all those type of 0s.

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

void change(vector<vector<int>> &grid, int x, int y, int c, int r)
{
    if (x < 0 || y < 0 || x > r - 1 || y > c - 1 || grid[x][y] == 1)
        return;

    grid[x][y] = 1;

    change(grid, x + 1, y, c, r);
    change(grid, x, y + 1, c, r);
    change(grid, x - 1, y, c, r);
    change(grid, x, y - 1, c, r);
}

void changeBorder(vector<vector<int>> &grid)
{
    int r = grid.size();
    int c = grid[0].size();

    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            if (i * j == 0 || i == r - 1 || j == c - 1)
            {
                if (grid[i][j] == 0)
                {
                    change(grid, i, j, c, r);
                }
            }
        }
    }
}

int findRoot(vector<int> &hashSet, int val)
{
    while (val != hashSet[val])
    {
        val = hashSet[val];
    }

    return val;
}

void Union(vector<int> &hashSet, int first, int second)
{
    int first_root = findRoot(hashSet, first);

    int second_root = findRoot(hashSet, second);

    if (first_root != second_root)
        hashSet[first_root] = second_root;
}

int closedIslands(vector<vector<int>> &grid)
{

    if (grid.size() == 0)
        return 0;

    int r = grid.size();
    int c = grid[0].size();

    changeBorder(grid);

    vector<pair<int, int>> edges;

    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {

            if (grid[i][j] == 0)
            {
                int id = i * c + j;

                if (j + 1 < c)
                {

                    if (grid[i][j + 1] == 0)
                    {
                        int right = i * c + j + 1;
                        edges.push_back({id, right});
                    }
                }
                if (i + 1 < r)
                {

                    if (grid[i + 1][j] == 0)
                    {
                        int down = (i + 1) * c + j;
                        edges.push_back(make_pair(id, down));
                    }
                }
            }
        }
    }

    vector<int> hashSet(r * c, 0);
    for (int i = 0; i < r * c; i++)
    {
        hashSet[i] = i;
    }

    for (auto edge : edges)
    {
        Union(hashSet, edge.first, edge.second);
    }

    int numComponents = 0;

    for (int i = 0; i < r * c; i++)
    {
        if (grid[i / c][i % c] == 0 && hashSet[i] == i)
            numComponents++;
    }

    return numComponents;
}

int main()
{
    int r, c;
    cin >> r >> c;
    vector<vector<int>> grid(r, vector<int>(c));
    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            cin >> grid[i][j];
        }
    }

    cout << closedIslands(grid);
    return 0;
}

The time and space complexity of the above program will be O(r*c)

By now you would have a complete understanding of how to solve this problem.