In this article, we have explored an insightful approach/ algorithm to find the number of interior integral points of a triangle. This is an important concept in the field of computational geometry.

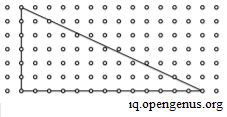
TABLE OF CONTENTS

• Problem Statement Definition
• Intuition
• Pick's Theorem
  • Mathematical Formulation
• Solution Analysis
  • Area of a triangle
  • Integral points on a line segment
    • Naive approach
    • Optimized approach
• Algorithm
• Implementation
  • Python
  • C++
• Time-Complexity analysis
• Space-Complexity analysis
• Applications

Reading time: 25 minutes | Coding time: 15 minutes

Let us dive right into the solution!

PROBLEM STATEMENT DEFINITION

To put the problem in simpler words- We are given the x and y coordinates of the three vertices of a triangle. We need to find the number of integral coordinates inside the triangle.

Let us understand this with an example:
Suppose we have are given the cooridinates as (0,0) , (0,7) and (4,5). Let us plot the points.

Let us construct the triangle:

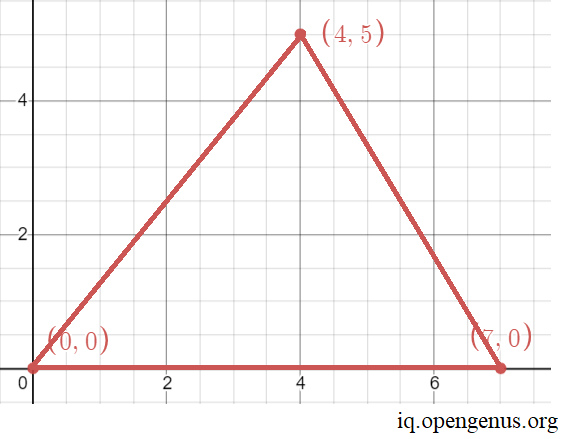
Now, let us plot the interior integral coordinates,

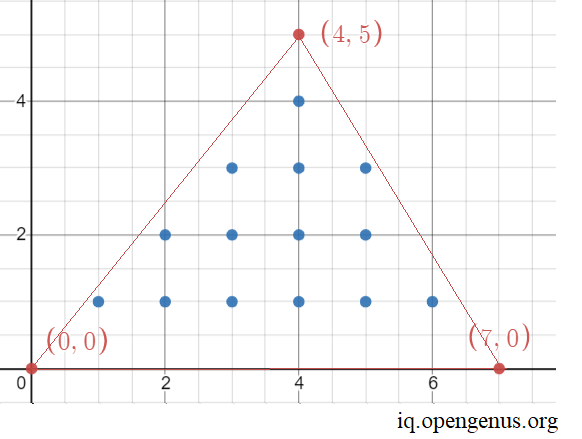
Thus, we can plot 14 points which are integers. Thus the solution for the points: (0,0) , (0,7) and (4,5) is 14.

INTUITION

Intuitively, it is not an easy task to implement a program to calculate the interior integral points. There are no naive methods for solving this problem. If only there was a simple formula that could easily give us the answer we are looking for!

PICK'S THEOREM

Austrian mathematician Georg Alexander Pick, in 1899, gave us a formula to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.

For any general polygon, Pick's theorem provides a way to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.

Since a triangle is a polygon, the formula can be applied for our problem statement.

Mathematical Formulation

We are given a certain polygon with non-zero area. We denote its area by A, the number of points with integer coordinates lying strictly inside the polygon by I and the number of points lying on polygon sides by B.

Thus, the Pick's formula states that:
i.e, Area of a polygon = (Integral interior points)+((Integral points on the edges)/2)−1

A = I + B/2 -1

You can go through the proof for the theorem here

SOLUTION ANALYSIS (identifying sub-problems)

From pick's theorem, we can deduce that the number of interior integral points

I = (2A - B + 2) / 2.

Thus the two sub-problems are to find the:

1. Area of the triangle
2. Number of interior integral points

Let us find their optimal solutions!

1. Area of a triangle

This is a standard middle school formula:

Expanding the determinant, we get:
A = (1/2) [x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3(y1 – y2)]

Note: For floating point to integer precision however, to get the correct value we find d_area (i.e [x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3(y1 – y2)] ). We then divide by 2 (i.e area = d_area/2)

2. Number of integral points on the edges of the triangle

Let us reduce the problem to Number of integral points on a line. To understand, let us take an example. Consider two points (-1,4) and (6,4). Let us plot the points.

Let us visually note and plot the integral points on the line.

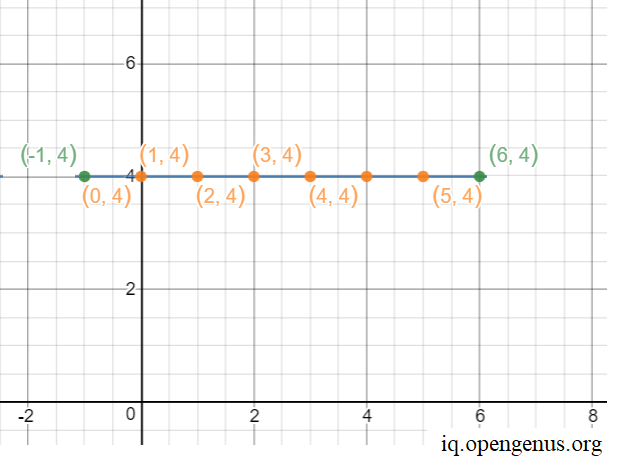
Thus, there are 6 points on the line.

To solve this sub-problem, here are two approaches.

Naive approach

• Read the input of two points.
• Initialize a count variable to zero.
• Consider any one of the two given points.
• Reach the other end point by using a loop incrementing by 1.
• For every point inside the loop, check if it lies on the line that joins given two points.
• If yes, then increment the count by 1.

Optimized (GCD) approach

The line can be divided into one of three distinct categories

• If edge is parallel to the Y-axis, then the number of integral points in between is : abs(p.x - q.x)-1
• If the edge formed by joining p and q is parallel to the X-axis, then the number of integral points between the vertices is : abs(p.y - q.y)-1
• Else, we can find the integral points between the vertices using below formula: GCD(abs(p.x - q.x), abs(p.y - q.y)) - 1

The above formula is a well known and can be proved using simple geometry. This approach works on the idea that shifting the edge such that one of the vertex lies at the origin does not change the characteristics that make the calculation of its intgral points.


In other words, it is easier to calculate the answer when coefficients a, b and c in the equation:
ax + by +c = 0 become co-prime. This can be achieved by calculating the GCD (greatest common divisor) of a, b and c. This converts the coefficients to the simplest form.Then, the answer will be y2-y1/(a-1) because after calculating ax + by + c = 0, for different y values, x will be number of y values which are exactly divisible by a.

Below is the psuedocode for this approach.

int gcd(int a, int b)
{
    if (b == 0)
       return a;
    return gcd(b, a%b);
}
 
int getCount(Point p, Point q)
{
    if (p.x==q.x)
        return abs(p.y - q.y) - 1;
    if (p.y == q.y)
        return abs(p.x-q.x) - 1; 
    return gcd(abs(p.x-q.x), abs(p.y-q.y))-1;
}

Now that we have identified the sub-problems and their optimal solutions, let us move onto the bigger picture - finding the number of Integral points inside a triangle using pick's formula.

ALGORITHM

• Read the input points as three sets of x and y coordinates (namely x1,y1 , x2,y2 and x3,y3)
• Find the area of the traingle using the formula mentioned previously and assign it to A
• Find the number of integral points on the three line-segments connecting the vertices using the algorithm mentioned above and intialize it to B.
• Find the number of interior integral points (I) by applying the formula mentioned above.

IMPLEMENTATION

1. Python code:

class Point:
 
    def __init__(self, x, y):
        self.x = x
        self.y = y
         

def gcd(a, b):
 
    if (b == 0):
        return a
         
    return gcd(b, a % b)
 

def Integral_points_on_line(p, q):
     
    
    if (p.x == q.x):
        return abs(p.y - q.y) - 1
    if (p.y == q.y):
        return abs(p.x - q.x) - 1
 
    return gcd(abs(p.x - q.x),
               abs(p.y - q.y)) - 1
 

def Integral_interior_points(p, q, r):
 
    BoundaryPoints = (Integral_points_on_line(p, q) +  Integral_points_on_line(p, r) + Integral_points_on_line(q, r) + 3)
    d_Area = abs(p.x * (q.y - r.y) + q.x * (r.y - p.y) +r.x * (p.y - q.y))
    return (d_Area - BoundaryPoints + 2) 
 

if __name__=="__main__":
     
    p = Point(0, 7)
    q = Point(4, 5)
    r = Point(0, 0)
     
    print("Number of integral points inside given triangle is ", Integral_interior_points(p, q, r))
    

2.C++ code:

#include<bits/stdc++.h>
using namespace std;
struct Point
{
    int x;
    int y;
};
 

int gcd(int a, int b)
{
    if (b == 0)
       return a;
    return gcd(b, a%b);
}
 
int Integral_points_on_line(Point p,Point q)
{
    if (p.x==q.x)
        return abs(p.y - q.y) - 1;
    if (p.y == q.y)
        return abs(p.x - q.x) - 1;
 
    return gcd(abs(p.x-q.x), abs(p.y-q.y)) - 1;
}
 
int Integral_interior_points(Point p, Point q, Point r)
{
    
    int BoundaryPoints = Integral_points_on_line(p, q) + Integral_points_on_line(p, r) + Integral_points_on_line(q, r) + 3;
    int d_Area = (abs(p.x*(q.y - r.y) + q.x*(r.y - p.y)  +  r.x*(p.y - q.y)));
    return (d_Area - BoundaryPoints + 2)/2;
}
 

int main()
{
    Point p,q,r;
    p.x=0;
    p.y=0;
    q.x=7;
    q.y=0;
    r.x=4;
    r.y=5;
    cout << "Number of integral points inside given triangle is "<< Integral_interior_points(p, q, r);
    return 0;
}

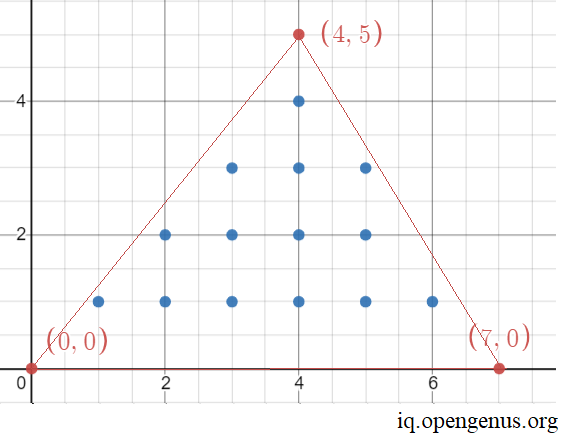
OUTPUT:

Number of integral points inside given triangle is 14

The solution given by the program is:

TIME-COMPLEXITY ANALYSIS

The time-complexity of GCD algorithm is O(loga)+O(logb) if we are finding the GCD of a and b.
Finding the integral points on the edges runs in constant time.
Substituting the values in Pick's formula and finding the Number of integral points inside the given triangle also takes constant time.
Hence, the driver of the overall time-complexity is GCD.

• Worst case time complexity: Θ(2* (log n) ) , when a=b=n or b=c=n or c=a=n and n is large
• Average case time complexity: Θ(log n) , when a,b and c are consecutive Fibonacci numbers
• Best case time complexity: Θ(1), when a is a multiple of b and b is a multiple of c, then Euclid GCD terminates in one call.

SPACE-COMPLEXITY ANALYSIS

The algorithm proposed does not use auxiliary space. Since, we do not use any extra space, the space complexity is Θ(1)

APPLICATIONS

• An extension of this algorithm is used by online battleships engine.
• An extension of this algorithm is used to calculate the pixels in a particular portion of a picture. This is done by dividing the portion with similar colour intensity into triangles.
• It is used used in other computational geometry problems.

With this article at OpenGenus, you must have the complete idea of Finding the Number of Integral points inside a triangle!