In this article, we will be working on finding number of subtrees whose nodes have same value, called universal value subtree or simply univalue subtree. Let's rewind our basics before moving on to the problem.

Binary Tree

A Binary tree is tree in which the root has maximum of two nodes,unlike in trees,where numerous nodes can be there.

What is universal value subtree?

Univalue tree : Tree having a same value for all the nodes and root too.

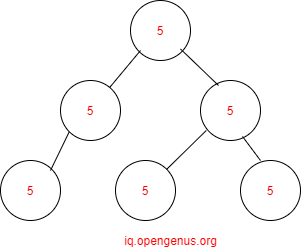
But binary tree given below is not universal.It has subtrees which have universal values.Leaves of a binary tree are always universal as they do not point to any node instead point to NULL.

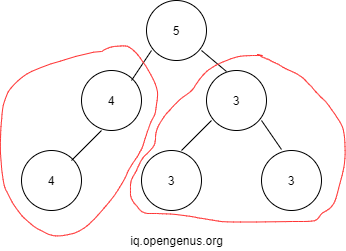
How many subtrees having universal values are present?
We count all the leaves due to the above mentioned reason and then subtrees with same values and non null nodes also.

• In tree-Subtree containing same values i.e.

    3           4
    /\    and  /
   3  3       4
  

  Number of such subtrees in the example=2 ------> 1st equation
• We will be counting the leaves i.e total no of leaves=3 -----> 2nd equation
• Therefore,total number of universal subtrees= 1st equation+2nd equation=2+3=5

Now, we will go through the algorithm we will be implementing to find the number of universal value subtrees.We will be using bottom-up or postorder traversal to find number of univalued subtrees.

Explanation

When is the subtree considered to be univalue subtree?

1. When the subtree's both left and right nodes values are equal to root's value.
2. When they are leaves i.e. left and right nodes are null.
3. When the left or right node is null but the existing right or left node has value equal to the root's value.
   When the subtree doesnt satisfy these three conditions , then it is not a univalue subtree.

Algorithm

1. Check if root is NULL.If true then return 0 as no roots are present.
2. Count Number of left and right subtrees by recursive calls.
3. Check if right or left subtrees returned are univalued.If no then return false.
4. Check if left or right nodes exist .
5. If right or left node's value is not equal to root's value then return false and dont count.
6. If any of the eliminating cases are not satisfied then its a univalue subtree, so increment the count.
7. Finally after checking on every node return the count.

PseudoCode

bool countUniValueST(root , count){
//basecase
check if root==NULL:
   return true
// all right & left subtrees through recursion and store whether they're univalued or not
bool left=countUniValueST(root->left, count)
bool right=countUniValueST(root->right , count)
//all possible cases when the subtree is not univalued:
if any of the left or right subtree is not univalued:
 return false
if right node exists and right[DATA] NOT EQUAL TO root[DATA]:
 return false
if left node exists and left[DATA] NOT EQUAL TO root[DATA]:
 return false
 
 //if any of the above conditions not satisfied:
 //increment subtree count
 count++
 return true
}

Now we will code this .

Code

#include <iostream>
using namespace std;
//binary tree structure
struct node{
int data;
struct node* left,*right;

};
bool findUniValueST(node *root , int &count)
{
  if(root==NULL)
     return true;
   bool right=findUniValueST(root->right,count);
   bool left=findUniValueST(root->left,count);
   //if left or right subtree is not univalued then that subtree is not univalued
   if(right==false||left==false)
   return false;
   //if right node exists and the value is not equal to root's value,again not univalued
   if(root->right && root->right->data!=root->data)
    return false;
    //same for left node also.
    if(root->left && root->left->data!=root->data)
    return false;
    /*if above possible conditions not satisified then its a univalued subtree.
    Like this we increment as and when there is a univalued subtree*/
    count++;
    /*and return true*/
    return true;
   
   
 }
 //to return count of the univalued subtrees.
 int countUniValueST(node *root ){
     int count=0;
     findUniValueST(root,count);
     return count;
 } 
//for inserting a new node 
node *newNode(int data){
     node *temp=new node;
    temp->data=data;
    temp->right=NULL;
    temp->left=NULL;
    return (temp);
}
int main() {
//sample input of the binary tree 
	struct node* root=newNode(1);
	root->left=newNode(3);
	root->right=newNode(3);
	root->left->right=newNode(3);
	root->left->left=newNode(3);
	cout<<"Number of univalued subtrees:"<<" "<<countUniValueST(root)<<endl;
	
	return 0;
}

Output:

Number of univalued subtrees: 4

Explanation of Output:

input :    1
          / \
         3   3
        / \
       3   3

Now by counting we know that there are 4 univalued subtrees.Since we are following bottom to up approach we first traverse to the leaves.According to the conditions they are counted as univalued.There are 3 leaves so univalued subtrees count is 3.
We will observe left part of the binary tree first.

  1 ----root
 /
 3 ---subroot
/\
3 3 ---both leaves

After counting in the 2 leaves(3,3) , they are checked if they are not equal to subtree's root data .As both are equal to subroot's data so count is incremented.

1 ---root
 \
  3 ---leaf

3 being leaf is counted as univalued.But its not equal to the root's value ,so its returned false.Now , as we have reached the root, we return the count of univalued subtrees which is 4.

Time Complexity:

This code follows a linear time complexity O(n), where n means the number of nodes of the tree.

Space Complexity:

Auxiliary space used is O(h) for the recursion call stack , where h is the height of the binary tree as we are recursively travelling till h height.

Now you know how to find number of universal subtrees using postorder traversal method.

Thank you.