In this article, we will discuss about algorithms to detect the orientation of three given ordered points. Orientation imply collinear, Clockwise or Anti-clockwise.

Table of contents

• Ordered points
• Orientation of three ordered points
• Complexity analysis
  
  

Ordered Points

A set of two numbers that are written in a particular order is called an ordered pair. they are also called as 2-tuples. The numbers are always enclosed within brackets (parantheses) and denotes both x coordinate and y coordinate. The first integer always represents the distance from the origin in x-axis. This is called the abscissa. The second integer represents the distance from the origin along the y-axis. And this is known as the ordinate.

Let us consider the point (3,7). Here, 3 is the abscissa and 7 is the ordinate. Sets of ordered points are extensively used in coordinate geometry to plot different geometric figures in the 2-D or 3-D plane for better understanding and are also used in statistics to plot graphs.

Orientation of three ordered points

Orientation of three ordered points refers to the different ways in which the three points can be placed in a given space. The three given points can be placed in such a way that when we connect them, they either form a triangle or a straight line. The former case has two orientations i.e. clockwise and anti-clockwise. These different orientations are represented pictorially below.

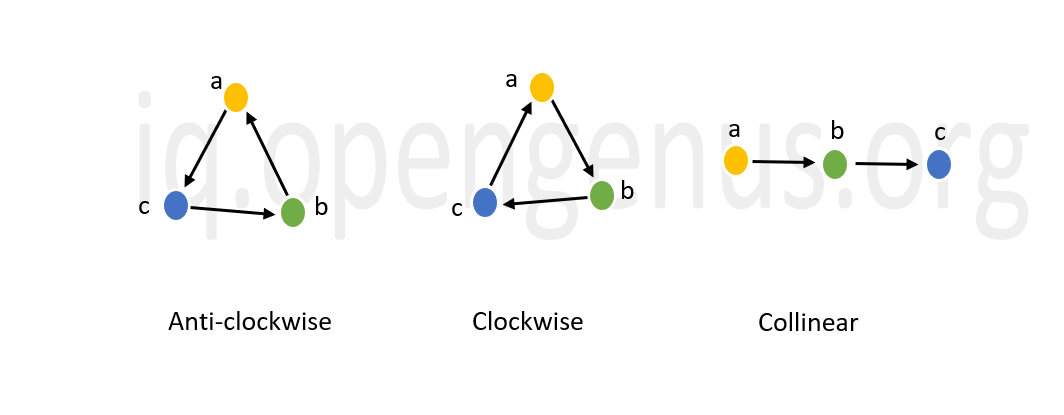
The next important question is how do we find the orientation of three given points? The answer is, by calculating the slope. Let us try to understand how to compute the orientation of the three ordered points.

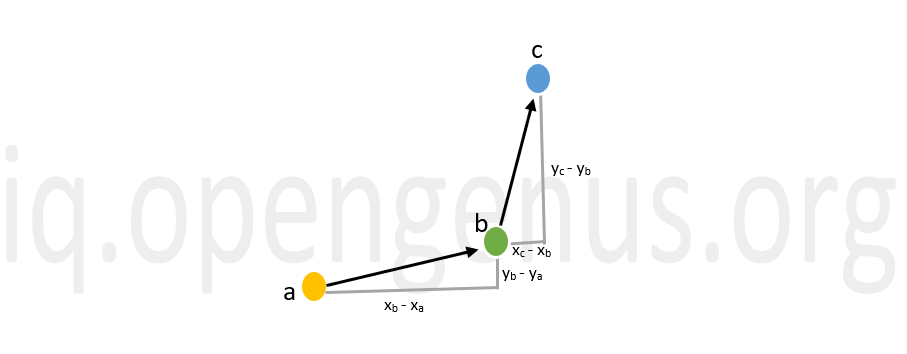
In the above given in=mage, we have 3 ordered points.

Slope of line segment (a,b) : θ = (y_b - y_a)/(x_b - x_a)
Slope of line segment (b,c) : φ = (y_c - y_b)/(x_c - x_b)

The orientation depends on the outcome of the expression (y_b - y_a)(x_c - x_b) - (y_c - y_b)(x_b - x_a) i.e. whether it is positive, negative or zero.

• If the outcome is zero, then θ = φ. Hence the orientation is collinear.
• If the outcome is negative, then θ < φ. Hence the orientation is anti-clockwise.
• If the outcome is positive, then θ > φ. Hence the orientation is clockwise.

Python implementation

For implementing the above discussed concept in python, we use class. First we declare a class Point which stores the point values passed as arguments of the class (initialization) and then declare a separate function where we pass the three points as arguments to perform the claculations and give us the result.

Class Point

# Stores the abscissa and ordinate of the point
class Point: 
    def __init__(self, x, y):
        self.x = x
        self.y = y

Function to find the orientation

def orientation(p1, p2, p3):
	
	val = (float(p2.y - p1.y) * (p3.x - p2.x)) - \
		(float(p2.x - p1.x) * (p3.y - p2.y))
	if (val > 0):
		# Clockwise orientation
		return 1
	elif (val < 0):
		# Anti-clockwise orientation
		return 2
	else:
		# Collinear orientation
		return 0

The result of the expression (y_b - y_a)(x_c - x_b) - (y_c - y_b)(x_b - x_a) is stored in val. The function returns the following values:

• 0 for collinear orientation
• 1 for clockwise orientation
• 2 for anti-clockwise orientation

Driver code

#Declaring the points

p1 = Point(0, 0) 
p2 = Point(2, 3)
p3 = Point(7, 10)

result = orientation(p1, p2, p3)

if (result == 0):
	print("Linear")
elif (result == 1):
	print("Clockwise")
else:
	print("CounterClockwise")

This is the driver code where we initialize the three points and call the orientation ( ) function to find the orientation of the three given points.

Output

Clockwise

C++ Implementation

In the C++ implementation, we use structure instead class that we used in python. The reason we use structure here even though structures and classes are functionally same is that, in C++ we commonly use structure for plain data as data members of a structure are of public accessibility mode by default. And classes are used when we make use of features like private or protected data members. The members of a class are of private accessibility mode by default in C++. Since we are declaring the points in the main function and they are in turn used in the orientation (), we prefer structure over class to make the problem easier.

Struct Point

#include <iostream>
using namespace std;
struct Point
{
    int x, y;
};

Here, we declare a structure Point which stores the abscissa and ordinate of the point.

Function to find the orientation

int orientation(Point p1, Point p2, Point p3)
{
  
    int val = (p2.y - p1.y) * (p3.x - p2.x) -
              (p2.x - p1.x) * (p3.y - p2.y);
 
    if (val == 0) return 0;  // collinear
 
 
    return (val > 0)? 1: 2; // clockwise or anti-clockwise
}

The result of the expression (y_b - y_a)(x_c - x_b) - (y_c - y_b)(x_b - x_a) is stored in val. We use conditional statement to find the orientation if it is not collinear.The function returns the following values:

• 0 for collinear orientation
• 1 for clockwise orientation
• 2 for anti-clockwise orientation

Driver code

int main()
{
	Point p1 = {0, 0}, p2 = {2, 3}, p3 = {7, 10};
	int result = orientation(p1, p2, p3);
	if (result == 0)	
    {
      cout << "Linear";
    }
	else if (result == 1) 
    {
      cout << "Clockwise";
    }
	else			 
    {
      cout << "Anti-Clockwise";
    }
	return 0;
}

This is the driver code where we initialize the three points and call the orientation ( ) function to find the orientation of the three given points and
also test the above function.

Output

Clockwise

Complexity analysis

The space complexity of the above program will be O(1) since no extra space is needed to store any duplicate data structure.

The above implementation uses two operations: subtraction and multiplication. The time complexity of subtraction of two N-digit integers is O(N) and the time complexity of two N-digit numbers is O(N log N). So, the overall Time Complexity is O(N logN) if N digit numbers are used to represent the points.

With this article at OpenGenus, you must have the complete knowledge of Orientation of three ordered points.