In this article, we have explored an insightful approach/ algorithm to find a simple closed path in a set of points. This is an important concept in the field of computational geometry.

Reading time: 25 minutes | Coding time: 20 minutes

TABLE OF CONTENTS

• Problem Statement Definition
• Intuition
• Solution Analysis
  • Orientation
  • Intersection of line segments
  • Ordering of points
• Implementation
• Complexity analysis
  • Time-Complexity
  • Space-Complexity
• Applications

PROBLEM STATEMENT DEFINITION

To put the problem in simpler words- Given a set of points, connect the dots without crossing. This should not be confused with convex hulls. We just need to connect** all the points** with the constraint that two connecting edges do not intersect.

Let us understand this with an example:
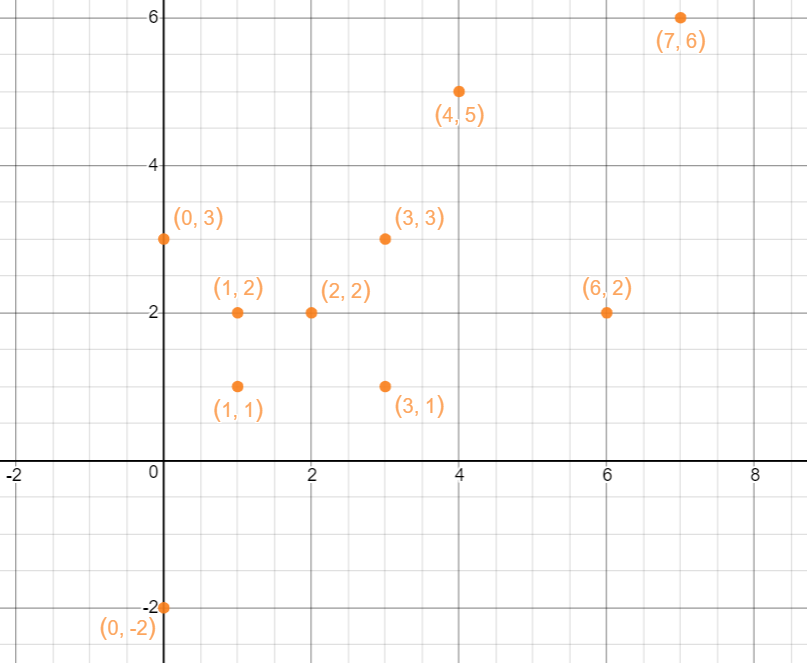
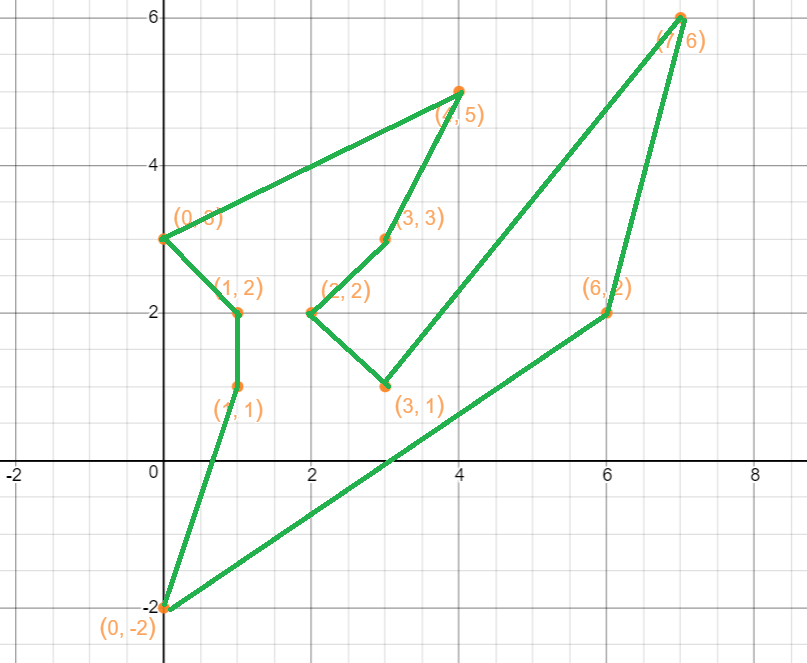
Suppose we have an array with 10 points:
{0, 3}, {7,6}, {1, 1}, {2, 2}, {6,2}, {4, 5}, {0, -2}, {1, 2}, {3, 1}, {3, 3}

Let us plot them:

As mentioned earlier, the problem is not to find the convex hull which would look like this.

Instead we have to find a closed path which connects all the points. The path can be arbitrarily constructed but the edges connecting two points should not intersect and the path should be closed!

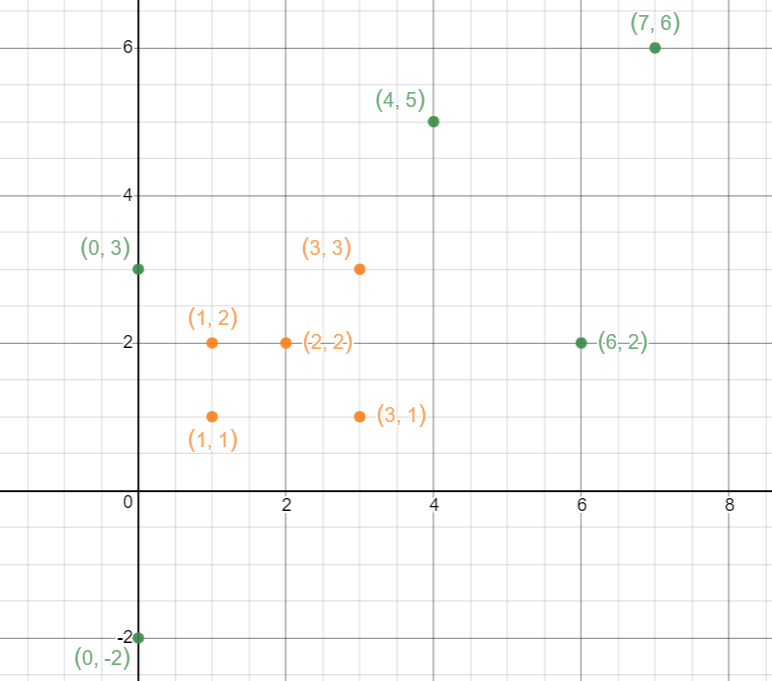
Possible solutions are:

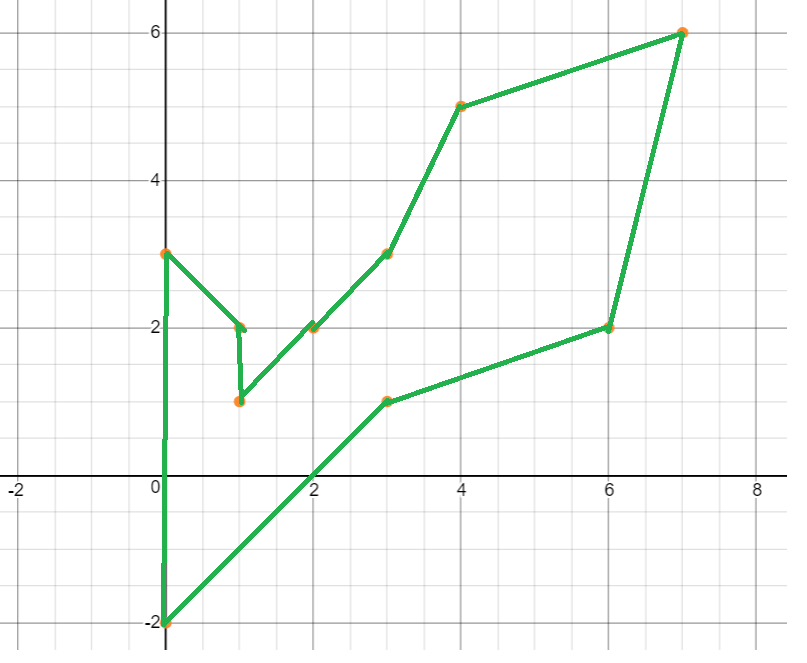
However, the following attempts are invalid.
.

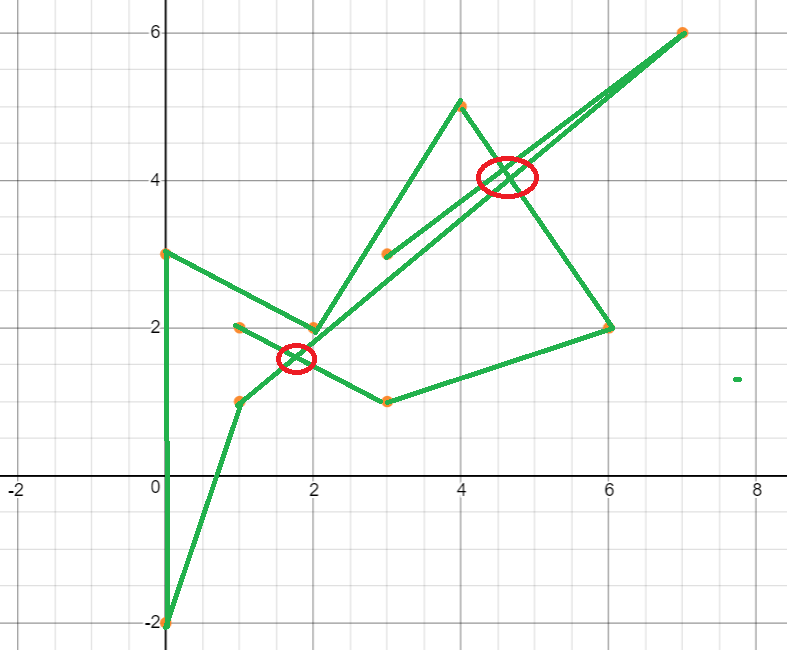The path is not closed and the edges intersect (shown within the circle)

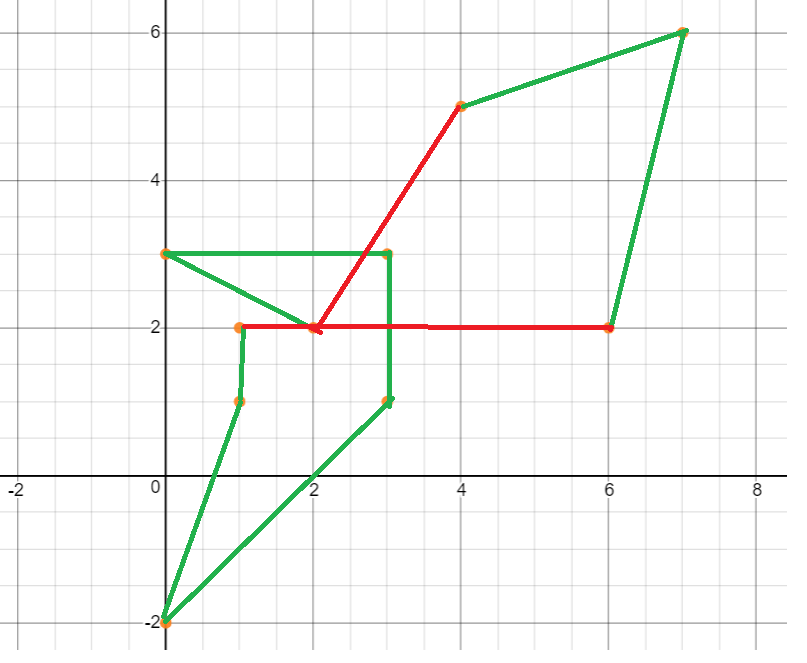
The edges connecting the points intersect. The valid edges of the path are shown in green and the invalid points are shown in red.

Now that we know what the solution should be let us go on a journey to reach the answer!

INTUITION (Identifying sub-problems)

• The idea is simple. We need to start connecting points while checking if the line segment intersects with any other segment. So our sub-problem (probably the biggest problem in this question) is to know when the line-segments connecting two points intersect. Let us discuss this shortly.

• The other problem is to know from which point to start from. This is an important point to consider because the point we arbitrarily choose might be the most complex route of our path. It is important to understand that backtracking is not a good approach in solving geometric problems. We can start constructing our path from the arbitrarily chosen point but we might reach a deadlock condition where we have to intersect with another line segment to form a path. Thus another important problem is to effectively choose the starting point and the order of the points thereafter.

SOLUTION ANALYSIS

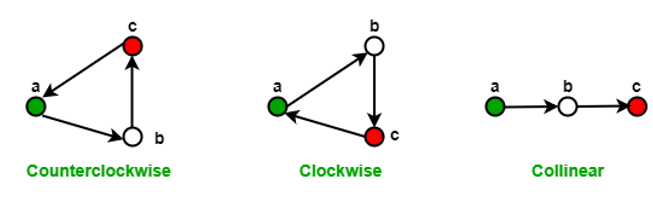
Orientation:

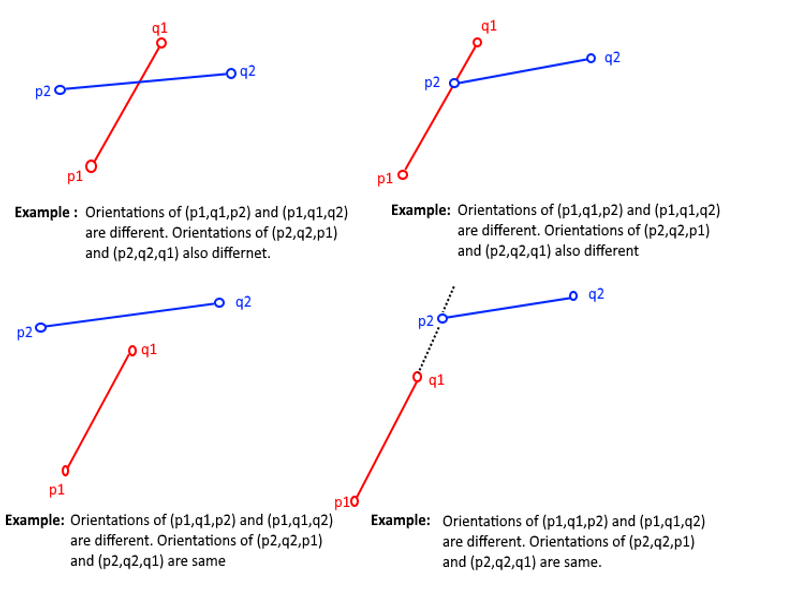
Before we move on to intersection of lines, let us first know about the orientation of a triplet of points in a plane:

Orientation of an ordered triplet of points in the plane can be

• counterclockwise
• clockwise
• collinear

The following diagram shows different possible orientations of (a,b,c)

How do we find the orientation of two line segments?

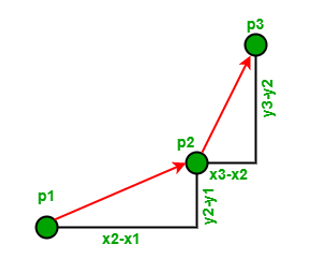
The idea is to use slope. Let us show this using an example.

The slope for line (p1,p2) = (y2 – y1)/(x2 – x1)
The slope for line (p2,p3) = (y3 – y2)/(x3 – x2)
For three points to be collinear, the slopes are same, we have :
=> (y2 – y1)/(x2 – x1) = (y3 – y2)/(x3 – x2)
=> (y2 – y1)(x3 – x2) = (y3 – y2)(x2 – x1)
Hence we get,
=> (y2 – y1)(x3 – x2) – (y3 – y2)(x2 – x1) = 0

Extending this concept,
Let the lope of line segment (p1, p2) be σ = (y2 - y1)/(x2 - x1)
Let the slope of line segment (p2, p3) be τ = (y3 - y2)/(x3 - x2)

Using above values of σ and τ, we can conclude that, the orientation depends on sign of below expression: (y2 - y1)(x3 - x2) - (y3 - y2)(x2 - x1)

• Above expression is zero when if σ = τ, i.e., the points are collinear
• Above expression is positive when σ > τ, the orientation is clockwise (right turn)
• Above expression is negative when σ < τ, i.e., orientation is counter-clockwise (left turn)

Psuedocode for orientation

int orientation(Point p, Point q, Point r)
{
    int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
 
    if (val == 0) return 0;  // collinear
    return (val > 0)? 1: -1; // clockwise or counterclock wise
}

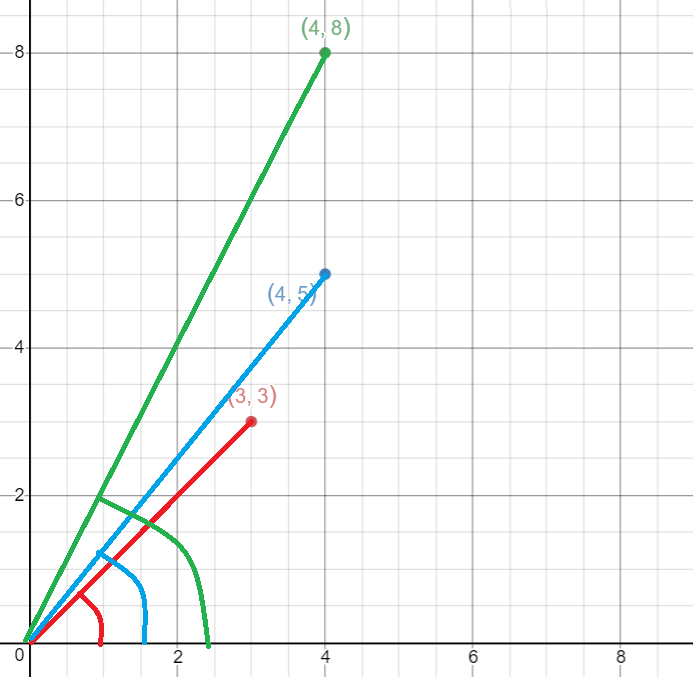
Intersection of lines:

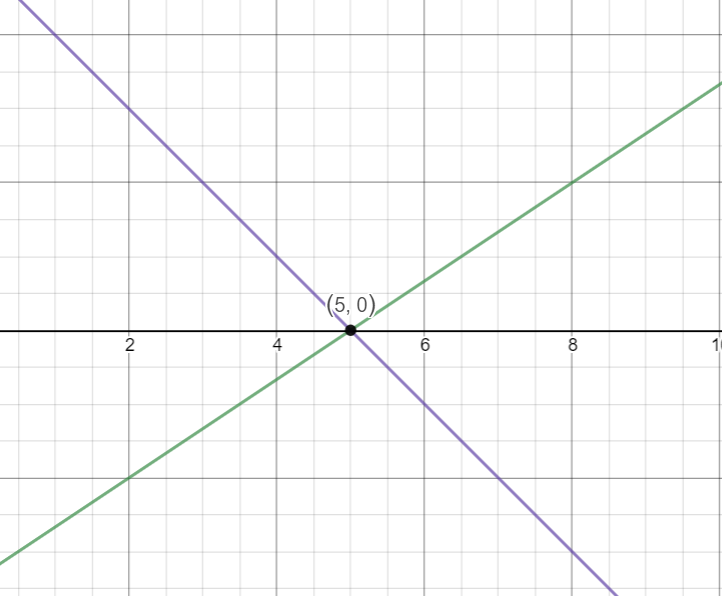
Let us dive right back into middle-school geometry. Let us consider two line segments (marked with green and purple).

We see that they intersect at (5,0)

Although it is intuitive that they intersect, To mathematically show it we use the aforementioned orientation concept.

Straddling

A line (let's call it L) divides the plane into two parts (half-planes is a term we use). A line segment has two endpoint, say P1 and P2. If the two endpoints are neither of them on the line, and instead the two endpoints are in different parts of the plane as divided by L (different half-planes), then we say the line segment P1-P2 "straddles" line L. If you've ever straddled a bicycle, you know about having your two feet on opposite sides of the bicycle.

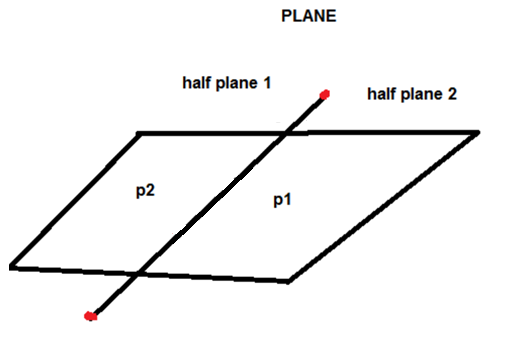
How is Orientation useful here?

Straddling can be explained in terms of orientation. Two segments (p1,q1) and (p2,q2) intersect if the following two condition is verified

• (p1,q1,p2) and (p1,q1,q2) have different orientations
• (p2,q2,p1) and (p2,q2,q1) have different orientations.

This is how we check if two line segments intersect in this problem.

Ordering of points:

As mentioned earlier, we need an efficient ordering method to effectively solve this question. The best known approach is to sort the points based on their polar angles in counter clockwise direction.

In our program, we sort by polar angles in a different way following the steps mentioned below:

• We sort the points in increasing y coordinate values.
• If two points have the same y coordinate then the point having lower y coordinate is the predecessor of the other point.

By virtue of this ordering approach, the points mentioned in the first example:
{0, 3}, {7,6}, {1, 1}, {2, 2}, {6,2}, {4, 5}, {0, -2}, {1, 2}, {3, 1}, {3, 3} will be sorted as:
{0, -2}, {1, 1}, {3, 1}, {1, 2}, {2, 2}, {6,2}, {0, 3}, {3, 3}, {4, 5}, {7,6}

The advantage of this ordering approach is that we do not have to check for intersection for every iteration.

Now that we have all sub-problems covered, let us jump into the execution of the program.

ALGORITHM

The algorithm steps are:

• Read the input points.
• Sort the points considering the steps mentioned above.
• Find the bottom left point as P
• Traverse the sorted list of points checking if the line segment joining two points intersects with any other segment using the steps mentioned above.

IMPLEMENTATION:

Let us have a look at the implementation of this algorithm in C++

#include <bits/stdc++.h>
using namespace std;

class Point {
   public:
   int x, y;
};
Point p0;

int orientation(Point p1, Point p2, Point p3) {
   int val = (p2.y - p1.y) * (p3.x - p2.x) - (p2.x - p1.x) * (p3.y - p2.y);
   if (val == 0) return 0; 
   return (val > 0)? 1: 2; 
}


int euclid_dist(Point p1, Point p2) {
   return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}


int compare(const void *vp1, const void *vp2) {
   Point *p1 = (Point *)vp1;
   Point *p2 = (Point *)vp2;
   int o = orientation(p0, *p1, *p2);
   if (o == 0)
   return (euclid_dist(p0, *p2) >= euclid_dist(p0, *p1))? -1 : 1;
   return (o == 2)? -1: 2;
}

void find_Closed_Path(Point points[], int n) {
   int y_min = points[0].y, min = 0;
   for (int i = 1; i < n; i++) {
      int y = points[i].y;
      if ((y < y_min) || (y_min == y && points[i].x < points[min].x))
      y_min = points[i].y, min = i;
   }
   swap(points[0], points[min]);
   p0 = points[0];
   qsort(&points[1], n-1, sizeof(Point), compare); 
   cout<<"A simple closed path :"<<endl;
   for (int i=0; i<n; i++)
   cout << "(" << points[i].x << ", "<< points[i].y <<"), ";
   cout << "(" << points[0].x << ", "<< points[0].y <<")";
}
int main() {
   Point points[] = {{7,6}, {0, 3}, {1, 1}, {2, 2}, {6,2}, {4, 5}, {0, -2}, {1, 2}, {3, 1}, {3, 3}};
   int n = sizeof(points)/sizeof(points[0]);
   find_Closed_Path(points, n);
}

Output:

A simple closed path :
(0, -2), (6, 2), (3, 1), (7, 6), (3, 3), (4, 5), (2, 2), (1, 1), (1, 2), (0, 3), (0,-2) 

The simple closed path that we get following this algorithm is:

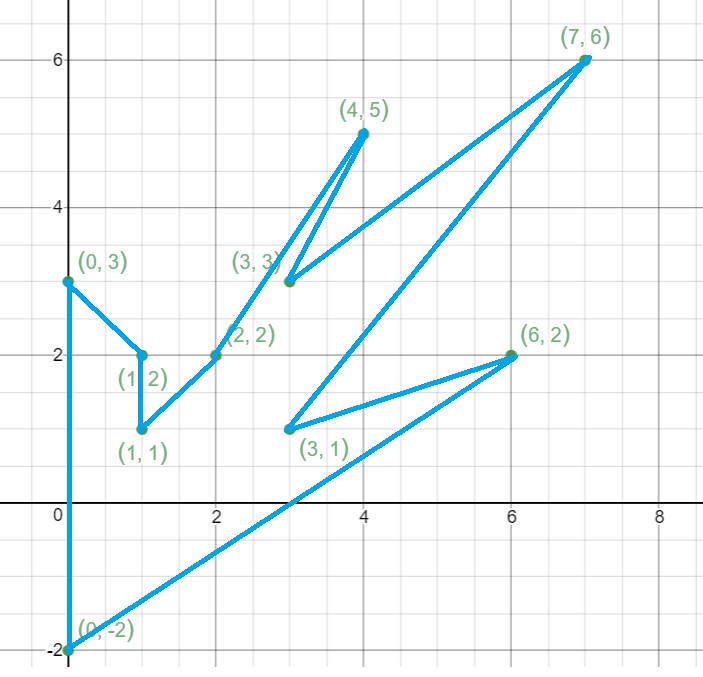
COMPLEXITY ANALYSIS

Time-complexity

The main steps involved in the algorithm and their time complexities are :
Sorting -> O(nlogn)
Checking orientation -> O(1)
Calculation the eucledian distance between points -> O(1)
Checking if line segments intersect -> O(1)

Thus the overall time complexity depends on the time complexity it takes to sort the points based on their polar angles.

• Worst case time complexity: Θ(nlogn)
• Average case time complexity: Θ(nlogn)
• Best case time complexity: Θ(nlogn)

Space-complexity

We do not make use of any auxiliary space. Hence the Space complexity is Θ(1)

APPLICATIONS

• An extension of this algorithm is used by simple 2-D games.
• It is used used in other computational geometry problems.

With this article at OpenGenus, you must have the complete idea of Finding simple closed path in a set of points!