
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we present the Mathematical Analysis of the Probability of Collision in a Hash Function. You will learn to calculate the expected number of collisions along with the values till which no collision will be expected and much more.
Table of content:
- Basics of Hash function + Collision
- Probability of collision
- Conclusions
Basics of Hash function + Collision
A Hash function converts a data (may be string, number, object) to a N-bit number. An ideal Hash function convert every unique data to a unique N-bit number (known as hash) and distributes data uniformly across all 2^N possibilities (as there are N bits).
To get basic idea of hash functions, go through these articles:
There are several standard Hash Functions like:
- MD5
- SHA-1, SHA-2, SHA-3
Some hash functions like SHA-1 are known to have loopholes so it should not be used in practice to avoid attacks on the system.
A ideal hash function is such that:
- Let hash of a data D be M. Given the hash value M, we cannot regenerate D.
- Hash of no two different data is same. This is not true as hash functions may be imperfect and due to space restriction, collision will take place.
What is Collision?
As inputs increase and the N-bits remain constant, there will be 2 data D1 and D2 whose hash value is the same. This is known as collision.
We want to know the probability of collision.
Probability of collision
Assume that the hash function H hashes to N bits. For example, SHA-256 hashs to 256 bits.
Then T = 2^N = number of unique hash values.
Assume we will hash M elements.
Probability(collision(T, M)) = Probability of collision with M elements being hashed by a hash function with T unique values.
Probability(collision(T, M)) = 1 - Probability(no_collision(T, M)) ... (equation 1)
Probability(no_collision(T, M)) = Probability of no collision with M elements being hashed by a hash function with T unique values.
Probability(no_collision1(T, M)) = Probability that Mth element does not collide with any of the previous values.
Probability(no_collision(T, M)) = Probability(no_collision1(T,1) * Probability(no_collision1(T,2) * … Probability(no_collision1(T,M)
Therefore, equation 1 becomes:
Probability(collision(T, M)) = 1 – Probability(no_collision(T,1) * Probability(no_collision(T,2) * … Probability(no_collision(T,M)
If there are V elements, then the next element will not collide with the previous V elements if it takes T – V positions.
Therefore, probability that i-th element does not collide is: (T-i)/T
as there are T-I slots left and T is the total number of slots.
Probability(collision(T, M)) = 1 – 1 * (T-1)/T * (T-2)/T * … * (T-M+1)/T
For i-th element, the probability of total number of collisions = (i-1)/T as there are i-1 previous elements which can collide and T is the total number of possible values.
Average probability of total number of collisions =
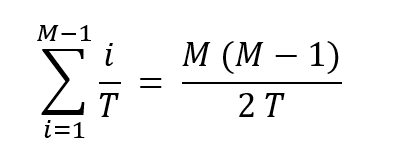
So, for 1 collision, we have:
M * (M-1) / 2T = 1
Based on this, the first collision will happen when:
M = √2 * √T
where:
- M = number of elements being hashed.
- T = total number of hash values in the hash function
This means if √2* √T elements are hashed, then we will see the first collision.
Note: T is the total number of possible hash values.
Therefore, if we use a 64 bit hash, then the total number of possible hash values will be 264. The first collision will take place when we insert √2* √T = 232.5 which is approximately 109 that is 1 trillion.
| Bits in hash value | Elements for 1st collision |
|---|---|
| 8 | 23 |
| 16 | 362 |
| 32 | 92,682 |
| 64 | 6,074,001,000 (6B) |
| 128 | 26,087,635,650,665,564,424 |
| 256 | 4.8 x 10^38 |
Hence, for bits >= 64, the number of elements required for 1st collision will be a significant value.
You can imagine or calculate that enormous number of elements that we need to hash to see the first collision if our hash function uses larger number of bits like 256 or 512 bits.
For two collisions, we have:
M * (M-1) / 2T = 2
M = 2 * √T
Similarly, for 3 collisions, we have:
M * (M-1) / 2T = 3
M = √6 * √T
For C collisions, we have:
M * (M-1) / 2T = C
M = √2C * √T
For all elements to collide that is M collisions, we have:
M * (M-1) / 2T = M
M = 2T
Therefore, for all elements to collide, the elements should be equal to twice the total number of hash values.
| Collisions | Elements to be hashed |
|---|---|
| 1 | 1.414 * √T |
| 2 | 2 * √T |
| 3 | 2.449 * √T |
| 4 | 2.828 * √T |
| M | 2T |
With this, you can see how the number of collisions increase with the increase in number of elements to be hashed.
If we hash M values and total possible hash values is T, then the expected number of collisions will be:
M * (M-1) / 2T = C
C = M * (M-1) / 2T
For example, if there are 2^16 = 65,536 = T and M = 2000, then the expected number of collision C is:
C = M * (M-1) / 2T
C = 2000 * (2000 - 1) / 2^17
C = 30.5 collisions
Conclusions
The conclusions of our analysis of collision of hash functions are:
- The first collision will take place when we hash N elements provided the total number of hash values is N^2.
- For all elements to collide, the elements should be equal to twice the total number of hash values.
- If we hash M values and total possible hash values is T, then the expected number of collisions will be C = M * (M-1) / 2T
Based on calculations in this article at OpenGenus, you see that hash functions are effective when more than 16 bits are in use and the total possible hash value is in a large range.
