Quick Sort is a Sorting Algorithm that takes a divide-and-conquer approach. We will be looking at how to do this while selecting two pivots points instead of one.

Contents:

• How to Quick Sort
• How to Partition for two pivot points
• Time & Space Complexity
• Extra

Pre-requisites:

• Quick Sort
• Time and Space complexity of Quick Sort
• Parallel Quick Sort
• Interview Questions on Quick Sort

Quick Sort

When performing Quick Sort their are two parts to it, first part of the Algorithm calls the second part ( the Partitioning ) and according to the partition it will recursively call it self for all available partition ( sub-array ), we're going to look at how this happens.

Steps to Quick Sort:

1. Check if the given array has more elements than 1.

If we get a sub-array that has only one element, then Ofcourse it's already sorted, So, we will just return without doing anything.
And this condition will be our stopping point for our recursion.

2. Do the partition.

If the sub-array follows the above condition then we need to find the position for pivot points ( which means we need to find sub-array to pass in next step ), partition should provide us the positions to the pivot points.
Read the how to partition", before 3rd step.

3. Now, call the quick-sort again on the created partition.

At this step we will have 3 partitions, and we will be calling the quick sort on all these partition,
let's have p1 and p2 as pointers to pivot points that we recieved in 2nd step.
and let's say that l and h is the starting and ending point of the sub-array we received in the beginning.

Now, make the following calls,

1. from l to p1 - 1.
2. from p1 + 1 to p2 - 1.
3. from p2 + 1 to h.

Psuedocode

function quick-sort(A, l, h):
    if l < h:
        p1, p2 = partition(A, l, h)
        quick-sort(A, l, p1 - 1)
        quick-sort(A, p1 + 1, p2 - 1)
        quick-sort(A, p2 + 1, h)

Note: that incrementing and decrementing p1 and p2 here, can lead to overflow which you will have to handle.

Three way Partition

The main piece of Quick Sort is to partition the array on some chosen pivot point, In our case, we will be choosing two pivot points, hence creating three partitions of the given array, For which we can use the Three-way Partition Algorithm which can partition the whole array in O(n) time without requiring any extra space.

Let's p1 and p2 be our pivot points, where,

• p1 = leftmost element of array
• p2 = rightmost element of array

Now, creating three-pointers,

• l to find the position for our p1
• h to find the position for our p2
• m` pointer for the element we are currently considering.

After considering all the above things, we should get and consider this scenario,

Three partitions:

• First partition contains all values that are less than and equal to the P1 and pointer l will point to it.
• Second partition will contain value that are greater than P1 and less than P2.
• Third partition will contain every value that are greater that and equal to the P2 and h will be pointing at P2.

You can see the m pointer at the end of the Second Partition, In Three-way partition we change the pointers according to the relation of the value that m is pointing, until the m becomes greater than the h.

Algorithm:

Now, let's arrange the whole thing in one and see how to do it.

1. Taking an array as A.
2. Let's save the starting pointer values of l and h, So, we could use them later ( We need this because provided l and h are not going to be always 0 and len - 1 ).
3. Take A[leftmost] as p1 and A[rightmost] as p2.
4. Check if p1 is greater than p2 if it is, then swap them.
5. Changing l to l + 1 and h to h - 1 ( This step will skip checking pivot points, we don't want them to shift at the very beginning of the partition ).
6. Setting m as the l.
7. Starting the loop until m < h and checking and performing the following:
   1. If the A[m] <= p1 then swap m and l and increment both l and m.
   2. If the A[m] >= p2 then swap m and h and then increment m and decrement h.
   3. And if the A[m] is greater than p1 and less than p2 then increment m.
8. After loop finishes, position the p1 and p2 at l - 1 and h + 1 respectively.

Psuedo-Code:

function partition(A, l, h):
    sl = l
    sh = h

    p1 = A[l]
    p2 = A[h]

    if p1 > p2:
        swap(A, l, h)
        p1 = a[l]
        p2 = a[h]

    l = l + 1
    h = h - 1
    m = l

    loop m <= h:
        if a[m] <= p1:
            swap(a, m, l);
            l += 1
            m += 1
        if a[m] >= p2
            swap(a, h, m)
            h -= 1
        else
            m += 1

    l = l - 1
    h = h + 1

    swap(a, sl, l)
    swap(a, sh, h)
    return (l, h)

Note: Partitioning of the array or the slice of the array should sort it, if the given array only contains two elements.

Time & Space Complexity

Best Case

While doing partitioning we're iterating through the whole elements of the array which takes O(N) time. And since, we're doing partition recursively on every 3 different partition, considering that the partition will happen evenly every time, the code should run O(log3N) times.
Therefore, resulting time for whole Algorithm would be:

$$O(NlogN)$$

Worst Case

It will be rare for worst case to occur, so much so, that one have to intentionally make the whole array in a manner that this could happen, but it's possible.
What causes this is when we end up choosing pivot points that does not create evenly distributed sub-partition, for example, if above in 3^rd step of Quick Sort we would have chosen p1 instead of p1 - 1 and p2 instead of p2 - 1 then running partition on the partition may produce only one or two sub-partition ( depending on the first pivot ).

So, if after partitioning we get only one sub-partition such as shown below, then we will be doing partition for $O(\frac{N}{2})$ times.

Therefore, resulting in Time Complexity of:

$$O(N^2)$$

Space Complexity

Since, the whole Quick Sort is done recursively, So, it's going to fill up the stack, and since, the recursion will occur for every sub-partition and since, that is O(log3N) .
Threrefore, the Space Complexity would be:

$$O(logN)$$

Extra

Like Yaroslavskiy’s Dual-Pivot Quick Sort algorithm, theirs also available 3-Pivot Quick Sort and theirs a paper written on multi-Pivot Quick Sort by Kushagra, explaining and comparing the Quick Sort Algorithms while calculating multiple aspects as such No. of swaps required and No. of comparisons required and No. of Cache Misses may happen.
Kushagra's paper also covers experiment results on different optimization levels of GCC.

For Example:

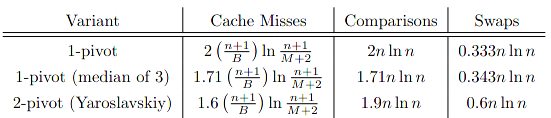
Note: I cutted out, 3-pivot from the above screen shot as a hint, for the reader to go and search for the paper and read it. Have Fun!