
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
This article delves into the illustrious Self Crossing problem and looks at how we can solve it. This can be solved efficiently using Computational Geometry ideas.
Table of Content
- Examining the Problem Statement
- Solving the Problem
- The Implementation
- Conclusion
Examining the Problem Statement
Given an array of integers, where each integer represents a distance. You start at coordinate (0,0) then for the length of the array. first, move array[0] meters to the north, then array[1] meters to the west, array[2] meters to the south, then array[3] meters to the east on and on such that after each move, the direction changes counter-clockwise.
return true if the final path formed crosses itself or false if it does not.
So we are given an array of distances and for each successive distance, we go counter-clockwise starting from the north i.e we first go up, then left, then right and then in that sequence until we have exhausted the array. We then have to check if the path formed crosses itself
For example, Given an array, [2, 3, 4, 6, 5] return true if the path formed will cross itself.
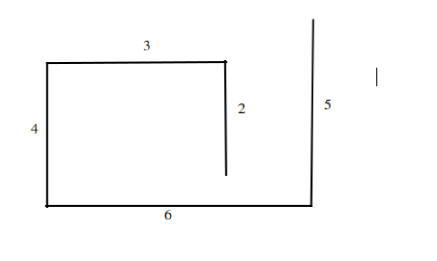
As can be seen, the path does not cross itself so we can safely return false.
Solving The Problem
The self crossing problem is not very intuitive at first glance, but it turns out once you get the logic it is not that hard to actually implement. The key thing to keep in mind is that we only have to detect a path cross once. We do not care about constructing the remaining path once a crossing has been found.
We have to try and figure out the cases that will result in a crossing. Let's examine the most basic states of the problem to see if we can extrapolate a pattern.
Case 1:
The earliest point we can get a crossing is if the 4th line crosses the 1st line as seen below. To put it more generally if the ith line crosses the i - 3 line we can return true
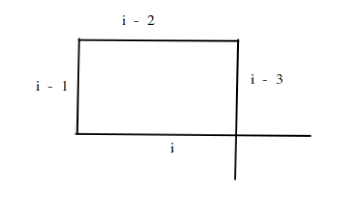
For this case to occur then the ith line has to be longer than the i - 2 line and the i - 3 line has to also be longer than the i - 1 line.
Case 2:
The next point we can get a crossing is if the fifth line overlaps with the 1st line or to put it more generally if the ith line crosses the i - 4 line then we can return true.
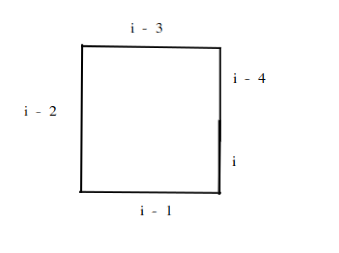
For this case to occur then the i - 3 line has to be equal to the i - 1 line and the i - 2 line has to be less than or equal to the sum of the ith and i - 4 line.
Case 3:
The next point we can get a crossing is if the sixth line intersects with the 1st line. Putting in generally, if the ith line crosses the i - 5 line then we return true.
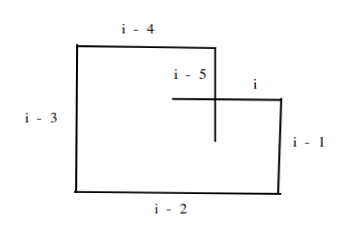
For this case to occur then the i- 4 line has to be less than the i - 2 line, the i - 2 line has to be less than the sum of the ith line and the i - 4 line, the i - 3 line has to be less than the sum of the i - 1 line and the i - 5 line and finally the i - 1 line has to be less than the i - 3 line.
It is guaranteed that no matter the size of the array, i.e how many lines the path is made up of. The path can only cross itself in one of the three cases. So, in order to implement our algorithm, all we need to do is iterate through the array starting from the 4th element until we get to the end of the array and at each iteration, we simply check if any of the 3 crossing conditions are met.
The Implementation
The above explanation is implemented succinctly in python below:
def isSelfCrossing(dist):
# starting the loop from the 4th element if there are less than 4 lines then a crossing
# is impossible so the loop will be skipped
for i in range(3, len(dist)):
# check for the first case; ith crosses i - 3 line
if dist[i - 2] <= dist[i] and dist[i - 1] <= dist[i - 3]:
return True
# the other two cases only get valid when the length of the array is greater than 4
if i > 3:
# check the 2nd case; ith line crosses i - 4 line
if dist[i-3] == dist[i-1] and dist[i-2] <= (dist[i] + dist[i-4]):
return True
if i > 4:
# check the 3rd case; ith line crosses i - 5 line
if dist[i-4] <= dist[i-2] and dist[i-2] <= dist[i] + dist[i-4] and dist[i-3] <= dist[i-1] + dist[i-5] and dist[i-1] <= dist[i-3]:
return True
return False
Conclusion
We have been able to tackle the self crossing problem. We saw how to solve it by looking at specific simple cases of the problem and were able to generalise our analysis to handle the general cases of the problem.
