
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have presented two algorithms to find the Shortest distance between a Line and Point in 3D plane. This involves idea of Projection and Parallelogram.
Table of contents:
- Introduction to Geometric Algorithms
- Shortest distance between a Line and Point in 3D plane
- First Approach (With Projection)
- Second Approach (With Parallelogram)
Let's learn something new. I hope here we all know something about three-dimensional geometry. So let's start practicing Geometric Algorithms.
Introduction to Geometric Algorithms
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Computational geometry and geometric algorithms are synonymous terms that denote an active discipline within computer science studying algorithms, or more generally the computational complexity of geometric objects and problems.
Use of Geometric Algorithms
Computer graphics, robot motion planning, computer games, simulations, geographic information systems, and CAD/CAM systems all use geometric algorithms to perform various tasks.
If you want to learn the real-world application of the geometric algorithm, you have to implement some geometric problems in your code. Let us start with our first problem.
Shortest distance between a Line and Point in 3D plane
Geometric Explanation:

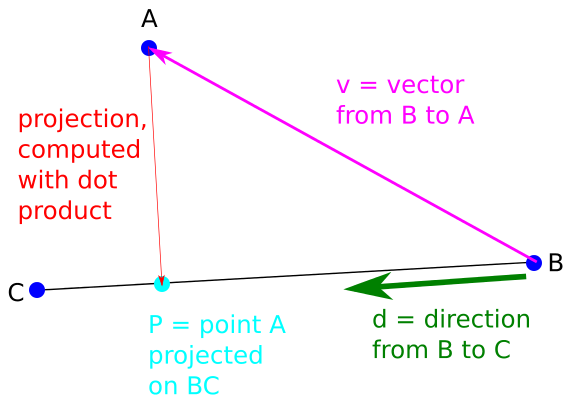
Here we have a line that passes through the two points B and C. And there is a point on the plane, named A. Now we need to find the shortest distance between the line and that point.
Key Point: The shortest distance from a point to a line is always the path that's perpendicular to the line, starting from the point.
So we need to find the perpendicular distance of the line from this point, But with that in mind, both the line and the point are in space.
Prerequisite:
Vector class:
property: (Co-ordinate) x,y,z
Behavior or Methods: add, subtract, magnitude, dot product,vectorProduct,unitVector,scalorProduct.
Vector Class
package com.example.opengenus.pointplanedist;
class Vector{
private double x,y,z;
public Vector(double x, double y, double z) {
this.x=x;
this.y=y;
this.z=z;
}
// getter method
public double getX() {
return x;
}
public double getY() {
return y;
}
public double getZ() {
return z;
}
// operation : add, subtract, magnitude, dot product,vectorProduct,unitVector,scalorProduct
public Vector add(Vector v) {
double x1= this.x+v.x;
double y1= this.y + v.y;
double z1= this.z+ v.z;
return new Vector(x1,y1,z1);
}
public Vector subtract(Vector v) {
double x1= this.x-v.x;
double y1= this.y - v.y;
double z1= this.z- v.z;
return new Vector(x1,y1,z1);
}
public double maginitude() {
double res= Math.pow(x, 2)+Math.pow(y,2)+Math.pow(z, 2);
return Math.sqrt(res);
}
public double dotProduct(Vector v) {
double resX = this.x *v.x;
double resY= this.y*v.y;
double resZ= this.z*v.z;
return (resX+resY+resZ);
}
public Vector vectorProduct(Vector v) {
double x1= (this.y)*(v.z) -(this.z)*(v.y);
double y1= (this.z)*(v.x) -(this.x)*(v.z);
double z1= (this.x)*(v.y) -(this.y)*(v.x);
return new Vector(x1,y1,z1);
}
public Vector unitVector() {
double mag= this.maginitude();
double x= this.getX()/mag;
double y= this.getY()/mag;
double z= this.getZ()/mag;
return new Vector(x,y,z);
}
public Vector scalarProduct(double num) {
return new Vector(num*this.x,num*this.y,num*this.z);
}
}
First Approach (With Projection)
We need to find the intersection point between the perpendicular line (which is passes through that point) and the given line.
The point is exactly the projection of A on the line.The distance between point A and the projection is the shortest.
Projection of a Point on a Line
Consider line AB and a point P. Construct a perpendicular PQ from P on AB that meets AB at Q. This point Q is known as the projection of P on the line AB.
Algorithm:
- Start
- Declare the required variables which denote the coordinates of the three points. Declare one additional variable for test cases.
- Read the input from the user.
- Create three Vector objects. (each for the given points)
- Find the direction ratio of the given line.
d=(C−B)/||C−B||
- Define a vector from B to A :
v=A−B - Computing the dot product (t) between
vand the directiond - Find the actual projection P of A on BC
P= B+ t⋅d
- Determine the shortest distance.
package com.example.opengenus.pointplanedist;
import java.util.*;
public class WithProjection {
public static void main(String[] args) {
/* Step 2: Declare the variables */
int x1,y1,z1,x2,y2,z2,x3,y3,z3,test;
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of test cases:");
test= sc.nextInt();
sc.nextLine();
while(test-->0) {
System.out.println("Input format :");
System.out.println("---------------");
System.out.println("1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.");
System.out.println("2. Point C(X3,Y3,Z3), any point in the plane");
System.out.println("Enter the co-ordinates of three points");
/* Step 3: Read the inputs*/
x1= sc.nextInt();
y1= sc.nextInt();
z1= sc.nextInt();
//////////////////////
x2= sc.nextInt();
y2= sc.nextInt();
z2= sc.nextInt();
/////////////////////
x3= sc.nextInt();
y3= sc.nextInt();
z3= sc.nextInt();
/////////////////
/* Step 4: Create three vector objects*/
Vector A= new Vector(x1,y1,z1);
Vector B= new Vector(x2,y2,z2);
Vector C= new Vector(x3,y3,z3);
/* Step 5 : Find the direction vector d */
Vector d= A.subtract(B);
d= d.unitVector();
/* Step 6 : Find one vector B to A */
Vector v= C.subtract(B);
/* Step 7: Find the dot product. */
double t= v.dotProduct(d);
/* Step 8: Find projection */
Vector p= B.add(d.scalarProduct(t));
/* Step 9: Determine the shortest distance. */
double ans= p.subtract(C).maginitude();
System.out.println("Shortest distance is: "+ans);
}
sc.close();
}
}
Output:
Enter the number of test cases:
3
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
5
2
1
3
1
-1
0
2
3
Shortest distance is: 5.0
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
4
2
1
3
2
1
0
2
0
Shortest distance is: 1.0
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
4
2
1
8
4
2
2
2
2
Shortest distance is: 1.632993161855452
Time and Space Complexity analysis
This algorithm has constant Time and Space complexity.
Time Complexity: O(1)
Space Complexity: O(1)
This is based on the assumption that arithmetic operations take O(1) time.
Second Approach (With Parallelogram)
In this case, we are going to use the vector product.
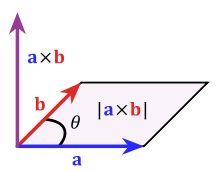
The vector product of Vector A and Vector B is of another vector perpendicular to them both.
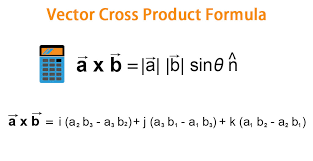
Key point:
Geometrically, that stands for the area of the parallelogram bounded by the vector a and b.
For this question, we know point A and from the straight line, the co-ordinate atleast one point (B, C) on the straight line.
We can determine the direction ratio of the straight line.
Follow this image:
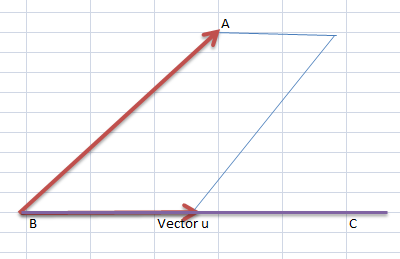
Now, the area of this parallelogram will be the vector product of AB and u (the direction vector of the line).But you know what,
The area of a parallelogram Base*Height.
And here the height of the parallelogram is the perpendicular distance of A from the line BC.The base is the length of vector u.
Let us assume the height is d.
Then ,
|BA x u| = |u|*d` or `d= |BA x u|/|u|
Algorithm:
- Start
- Declare the required variables which denote the coordinates of the three points. Declare one additional variable for test cases.
- Read the input from the user.
- Create three Vector objects. (each for the given points)
- Find the directional vector of the given line.
- Find BA vector.
- Find the vector product AC x d
- Find the shortest distance.
package com.example.opengenus.pointplanedist;
import java.util.Scanner;
public class WithParallelogram {
public static void main(String[] args) {
// TODO Auto-generated method stub
int x1,y1,z1,x2,y2,z2,x3,y3,z3,test;
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of test cases:");
test= sc.nextInt();
sc.nextLine();
while(test-->0) {
System.out.println("Input format :");
System.out.println("---------------");
System.out.println("1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.");
System.out.println("2. Point C(X3,Y3,Z3), any point in the plane");
System.out.println("Enter the co-ordinates of three points");
x1= sc.nextInt();
y1= sc.nextInt();
z1= sc.nextInt();
//////////////////////
x2= sc.nextInt();
y2= sc.nextInt();
z2= sc.nextInt();
/////////////////////
x3= sc.nextInt();
y3= sc.nextInt();
z3= sc.nextInt();
/////////////////
Vector A= new Vector(x1,y1,z1);
Vector B= new Vector(x2,y2,z2);
Vector C= new Vector(x3,y3,z3);
// find directional vector
Vector d= B.subtract(A);
// find AC vector
Vector AC = C.subtract(A);
// find the vector product AC x d
double vectorProduct = AC.vectorProduct(d).maginitude();
// find the distance
double distance= vectorProduct/d.maginitude();
System.out.println("Shortest distance is: "+distance);
}
sc.close();
}
}
Output:
Enter the number of test cases:
3
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
5
2
1
3
1
-1
0
2
3
Shortest distance is: 5.0
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
4
2
1
3
2
1
0
2
0
Shortest distance is: 1.0
Input format :
---------------
1. Point A(X1,Y1,Z1) and Point B(X2,Y2,Z2).The straight line passes through these two points.
2. Point C(X3,Y3,Z3), any point in the plane
Enter the co-ordinates of three points
4
2
1
8
4
2
2
2
2
Shortest distance is: 1.632993161855452
Time and Space Complexity analysis
This algorithm has constant Time and Space complexity.
Let's see some questions.
Question 1
What is the shortest possible distance between a point and a line in plane?
Perpendicular distance
Parallel distance
Distance from origin
None of these
The shortest distance from a point to a plane is along a line perpendicular to the plane.
Question 2
Which of the following is not an application of the geometric algorithm?
Tamper evident materials
CAD/CAM systems
Robot motion planning
Computer graphics
Tamper evident materials is a non-electronic innovation.
With this article at OpenGenus, you must have a complete idea of how to find the Shortest distance between a Line and Point in 3D plane.
