
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored Similarity Search on Big Vector Data along with Nearest Neighbor Search (NNS) or Approximate Nearest Neighbor Search (ANNS).
Table of contents:
- Introduction
- Definition
- Datasets
- Method
4.1. Directly Brute Force (for NNS)
4.2. LSH - Locality-Sensitive Hash (ANNS)
4.3. Graph-Based Algorithm (ANNS) - Summary
1. Introduction
Similarity search on vector data is a classical problem that have been researched for the past decades. In this problem, we have massive vector data as a "database", each vector represents a point in the hyperplane. A similarity search task is, given a new vector in or not in the database, we need to find the most (approximately) similar vector(s), and the similarity between two points is often calculate by L2 distance(Euclidean distance), inner-product or cosine distance. It's also known as Nearest Neighbor Search (NNS) or Approximate Nearest Neighbor Search (ANNS).
2. Definition
To be specific, vector data in such databases is produced by some neural networks, which means each vector is an embedding for a image/video/text. They may come from Bert, ImageNet, EfficientNet or any other DNNs.Nowadays, dataset's scale is explosively growing, we need to find a efficient way to solve the problem.
Let $N$ denotes the total number of vectors in such database, and
every element gets the same dimension $D$. Now we have a dataset $S = [s_{1}, s_{2}, s_{3}, ..., s_{N}]$ and every point $s_{i}$ represents a vector with dimension $D$, $s_{i} = [a_{0}, a_{1}, ..., a_{D-1}]$.
So the problem is, given a dataset S and a query vector $q$, find "Top-k" the most similar vector(s) T in S by calculate distance function.
$$
T = arg min _{T \subset S} \Sigma _{x \in T} d(x, q)
$$
Where $d$ is distance function and $d$ can be Euclidean Distance or Cosine Distance. We usually use the former i.e. L2 distance. When it comes to ANNS, the result T is not exact obtain from this equation.
L2 distance
$$
d(x, c) = \sqrt {\Sigma_{i=0}^{D-1}(x_{i} - c_{i})}
$$
where $x,c \in S$.
If we need exact result, it's NNS. If we need approximate result, it's ANNS.
3. Datasets
As mentioned above, datasets are embedding by neural networks. In this section, I'll list some famous datasets for NNS or ANNS here.
In last year, NeurIPS 2021 held a competition -
Billion-Scale Approximate Nearest Neighbor Search Challenge. In this game, some classical and new released datasets were listed. Such as BIGANN, SPACEV from Microsoft; DEEP, Text-to-Image from Yandex; SimSearchNet++ from Facebook, etc. Each dataset has 1 billion base point.
4. Method
We noticed that most of datasets get a big scale (1B) and the dimension of data is relatively high (96 - 256), even some "small" datasets, such as DEEP-1M, SIFT-1M and so on still own 1 million points. As a result of big scale dataset, search procedure needs to be accelerated by modern algorithm rather than brute force method. In front of these big vector data, we need a trade-off between accuracy and latency, so we propose ANNS. In ANNS, we allow the result points from search are not exactly the nearest point(s) of query, but ANNS provides the ability for online service because of low latency and tolerable error rate.
Following below methods are used for NNS or ANNS in past few years.
4.1 Directly Brute Force (for NNS)
This method was used to get exact answer from datasets. It requires a linear scan on the whole dataset, calculating function $d(q, x_{i})$ (mentioned in section 2) where $q$ is the coming query and $i$ in range(0, N-1). Then merge and re-ranking all result to obtain $K$ points which are exactly closest to query.
$$
Result \ R = argmin_{R \subset S} \Sigma_{i=0, x_{i} \in R} ^{K} {d(x_{i}, q)}
$$
4.2 LSH - Locality-Sensitive Hash (ANNS)
The main idea of using LSH to similarity search is simple. Assuming that two points $x$ and $y$ in high dimensional space are close, if there is a hash function $H$, then H(x) and H(y) may obtain the same result as long as they are close enough and function $H$ is appropriate.
4.3 Graph-Based Algorithm (ANNS)
Graph structure in search is more like a index. The well-designed index is used to perform suitable search algorithm.
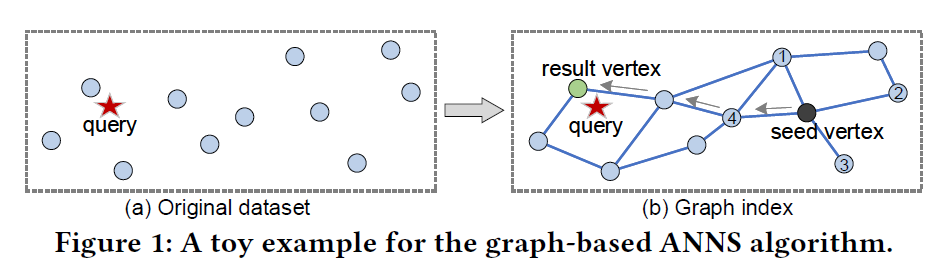
This Figure[1] above explains how graph-based algorithm works in similarity search. Each point in original dataset represents a vertex in graph, and they will be connected by some edge in specific strategy then we obtain a graph index. In particular, the method to choose neighbors for vertices is based on distance calculation, by evaluating function $d(x, y)$, the algorithm select suitable neighbors for every vertex. Usually, people expect to build an approximate KNN graph which means every node in graph connects to its k nearest neighbors. The famous algorithms of building graph includes HNSW, NSG and so on.
Having a graph index, we can run a search algorithm on it.
As Figure 1(b) shows, search algorithm will find a path from seed vertex to approximate nearest results when a query(read star in figure) comes. Seed vertex is a starting point for search, which can be specify or just random. For finding the appropriate path, Firstly, put seed vertex in to candidates list, then evaluate the neighbors of current node in that list then put the new nearest nodes into it. By doing this, we are approaching to the approximate results. It's like a greedy search but having difference.
Pseudo code. (not really available to use, because it's very complicate to implement a similarity search system)
Details can be find in DiskANN source code.
//search procedure, Pseudo code
/*
k - number of result needed (topK)
l - number of current nodes in candidates_list
l_size - size of candidates_list
candidate_list - vector (sorted by distance to query)
queue - priority queue
*/
init_candidate_list(candidate_list) // init list with seed vertex & it's neighbor
int k = 0;
while(k < l) {
int current_k = l;
if(!visited(candidate_list[k])) {
visit(candidate_list[k]);
Node current_node = candidate_list[k];
Neighbor current_neighbor = get_neighbor(current_node);
for( node in current_neighbor) {
double d = distance(node, query);
if(d > distance(query, candidate_list[l - 1] && l == l_size) {
continue;
}
int location = insert_into_list(node); // insert node to candidates_list in suitable locatoin
if(location < current_k) {
current_k = location;
}
if(l < l_size) {
++l;
}
}
if(current_k <= k) {
k = current_k;
} else {
++k;
}
} else { // visited;
++k;
}
}
return candidates_list[0:k];
5. Summary
To sum up, I'm going to explain why this technique is important. Similarity search is deployed in many fields, include recommendation system, search engine, information retrieval, face recognition, etc.
Think about you are building a face recognition system for weak security, and there are 1 million people needed to be involved. You can't tolerant high latency when a recognition request comes. We are unable to deal with massive data if we only rely on "brute force" search. Similar to information retrieval, a retrieval system won't be deployed as service if the search latency is too high to tolerant.
This is a brief introduction for KNN or ANN search, different storage strategies, product quantization, and other method are not discussed here. We can learn more in big-ann-benchmark.
References
[1]Wang, Mengzhao, et al. "A comprehensive survey and experimental comparison of graph-based approximate nearest neighbor search." arXiv preprint arXiv:2101.12631 (2021).
[2]Jayaram Subramanya, Suhas, et al. "Diskann: Fast accurate billion-point nearest neighbor search on a single node." Advances in Neural Information Processing Systems 32 (2019).
