Converting a Sorted Array to Binary Tree

Sorted array is converted to Binary Search Tree for faster search operations and querying. In this article we'll learn to convert any sorted array to binary search tree. For converting a sorted array to binary tree, we'll need an array which is unsorted and sort it first. Then we'll make the middle element of the array as the root of the tree and make the left children as the left subset of the array, similarly the right part will be the right subset of the array.

Implementation:

Let say we have an array A:

We'll sort this array by the inbuilt sort() function in standard template library in ascending order. First we'll take an array with name arr1 and fill the values {2,9,6,5,7,1,8,4} and sort it.

Code:

#include <bits/stdc++.h>
using namespace std;

int main(){
    vector<int> arr;
    int arr1[8] = {2,9,6,5,7,1,8,4};
    for(auto x:arr1) arr.push_back(x);
    sort(arr.begin(),arr.end());
    //Further code...
    
  
}

After sorting the array becomes,

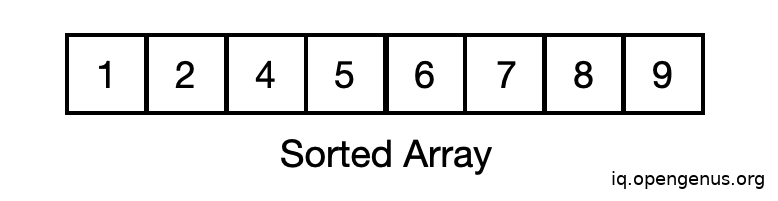
As the array is now sorted we can implement the tree data structure to store the values of the array elements.

Implementation of tree:

For the implementation of tree we need a Node class which defines a tree node to store data and pointers to left and right subtree.

So we can create a Node class by the following syntax:

class Node {
    public:
        int data;
        Node* left;
        Node* right;
}

After the creation of Node class we can implement the tree functions which are inserting nodes and traversing them.

Firstly, we'll need function to make an empty tree node in the memory,

Node* newNode(int data){
    // This line allocates the memory of a Node in the storage.
    Node* newnode = new Node();
    //This line sets the data into the node 
    newnode->data = data;
    //This line sets the left and right pointers to NULL
    newnode->right = NULL;
    newnode->left = NULL;
    return newnode;
}

Then we'll create a function which takes in an array or vector which is sorted as its input and creates a balanced binary search tree.

For implementation, we'll take vector as it's input and then find the mid element of the list, we'll take this element as root and find the mid elements of left and right subtree recursively to create a balanced tree.

Algorithm (recursive version):

1. Take a sorted array.
2. Find the mid element of the array, and insert into the tree.
3. Find the mid element of left and right tree, and insert into the array.
4. Repeat until no element is left.

Implementation of the above algorithm (recursive version) :

Step 1: Take a sorted array into the function.

Node* sortedArrayToBST(vector<int>& arr,  
                        int start, int end)  
{ 

Step 2: Find the mid element of the array, and insert into the tree.

    //If starting index goes beyond end index then return NULL
    if (start > end)  
        return NULL;  
  
    //Compute the middle index and make it as root.
    int mid = (start + end)/2;  
    Node *root = newNode(arr[mid]);  

Step 3 & 4: Find the mid element of left and right tree, and insert into the array. Repeat until no element is left.

    //Recursively create left and right subtrees.
    root->left = sortedArrayToBST(arr, start, mid - 1);  
    root->right = sortedArrayToBST(arr, mid + 1, end);  
    
    //Return the root element which is the middle element of the list
    return root;  
} 

Conversion from sorted array to BST takes n steps as the function has to go over every element once, hence the time complexity is O(n)
So the sorted array becomes,

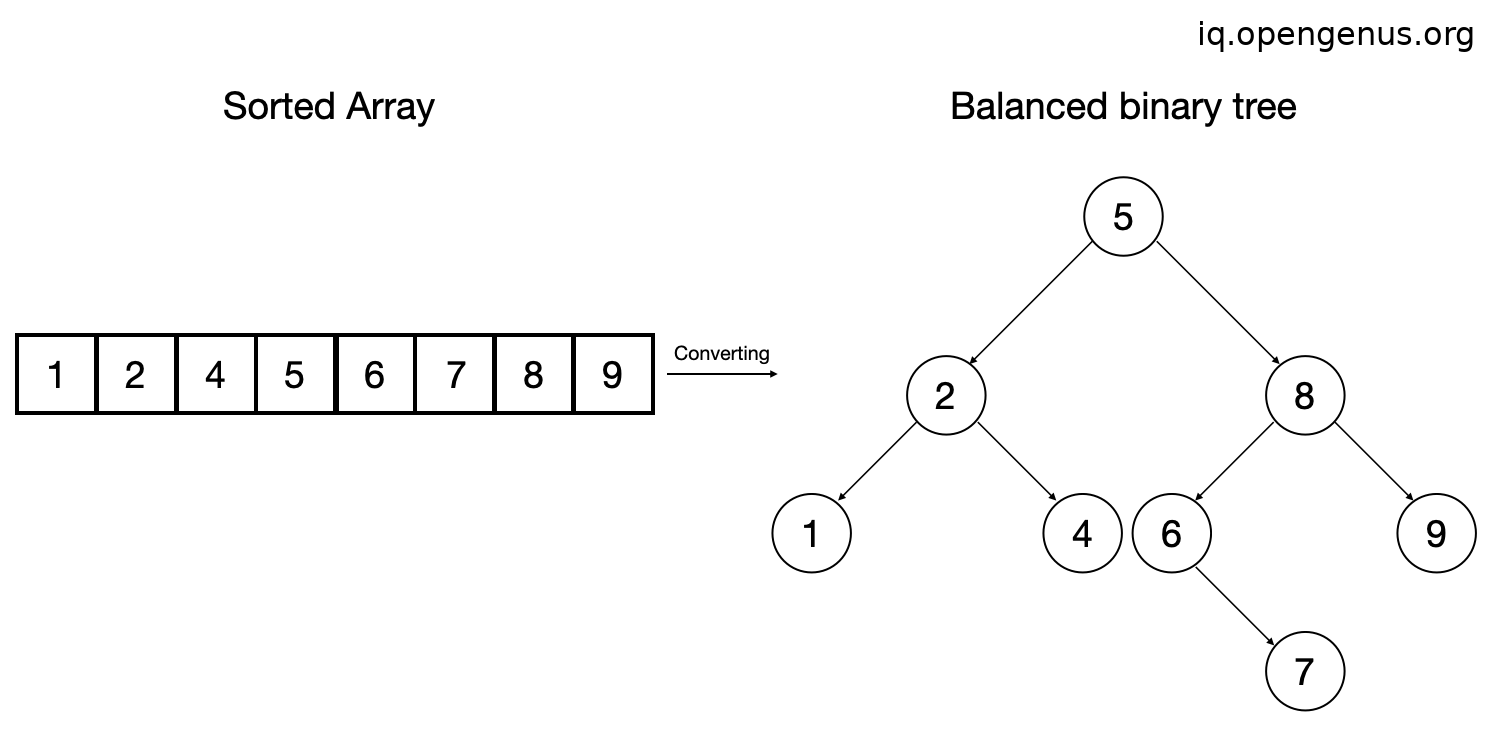
Algorithm (iterative version):

1. Take a sorted array and take a stack.
2. Each tuple keeps track of the child's parent and the side of the parent that the child will become.
3. We only push child tuples to the stack after their parents are created, the process will create the children until we reach the base case, whereby that branch has exhausted its corresponding chunk of the original nums.

Implementation of the above algorithm (recursive version) :

Step 1: First we'll create a struct T, with low_idx,high_idx and node.

struct T {
   int low_idx;
   int high_idx;
   Node node;
   Tree(int low, int high, Node _node) {
       low_idx = low
       high_idx = high
       node = _node
   }
}

Step 2: Then we'll create a function sortedArrayToBST.

Node sortedArrayToBST(int A[], int n) {

Step 3: Return if the length of array is 0

    if (n == 0)
        return NULL;

Step 4:Create stack and push the node with middle element of array.

    stack<int> S;
    Node root = new Node(A[(n - 1)/2])
    T tree = new T(0, n - 1, root)
    S.push(tree);
    while (!S.empty()) {

Step 5:Pop the top node and assign the left and right child to it.

        T tmp = S.top();
        S.pop();
        int mid = tmp.low_idx + (tmp.high_idx - tmp.low_idx) / 2;

Step 6: If the lower index of tmp element is less than mid we will pick middle element and push that into the tree.

        if (tmp.low_idx < mid) {
            Node node = new Node(A[tmp.low_idx + (mid - 1 - tmp.low_idx) / 2]);
            tmp.node.left_idx = node;
            tree = new T(tmp.low_idx, mid - 1, node);
            S.push(tree);
        }

Step 7:If the higher index of tmp element is greater than the mid we will pick middle element of high_idx and mid then push that into the tree.

        if (mid < tmp.high_idx) {
            Node node = new Node(A[mid + 1 + (tmp.high_idx - mid - 1)/2]);
            tmp.node.right_idx = node;
            tree = new T(mid + 1, tmp.high_idx, node);
            S.push(tree);
        }
    }
    return root;
}

Conversion from sorted array to BST takes n steps as the function has to go over every element once, hence the time complexity is O(n)
So the sorted array becomes,

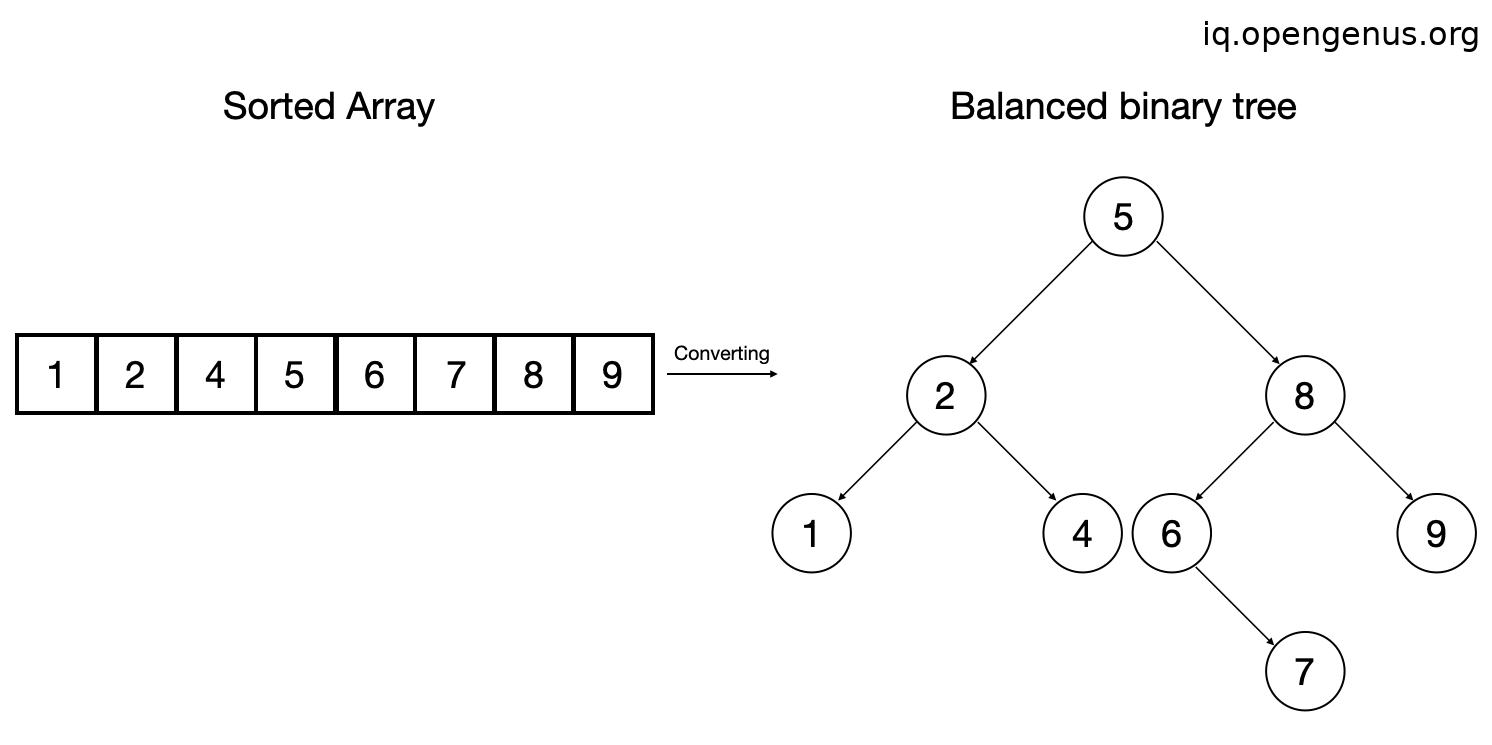
Now, you can implement various traversals such as inorder, preorder and postorder, for this example we'll demonstrate preorder traversal method.

In the preorder traversal method, first the root is traversed then the left subtree and then the right subtree.

We'll create a function for this purpose,

void preOrder(Node* root){
    if (!root) return;
    cout << root->data << " ";
    preOrder(root->left);
    preOrder(root->right);
}

Time Complexity: O(n)

Complete implementation:

So now the complete implementation of the conversion is as follows,

Including the header files

#include <bits/stdc++.h>
using namespace std;

Defining a class for Node

class Node {
    public:
        int data;
        Node* left;
        Node* right;
}

Defining a function for conversion of array to BST

Node* sortedArrayToBST(vector<int>& arr,  
                        int start, int end)  
{  
    //If starting index goes beyond end index then return NULL
    if (start > end)  
        return NULL;  
  
    //Compute the middle index and make it as root.
    int mid = (start + end)/2;  
    Node *root = newNode(arr[mid]);  
  
    //Recursively create left and right subtrees.
    root->left = sortedArrayToBST(arr, start, mid - 1);  
    root->right = sortedArrayToBST(arr, mid + 1, end);  
    
    //Return the root element which is the middle element of the list
    return root;  
} 

Preorder function for traversal

void preOrder(Node* root){
    if (!root) return;
    cout << root->data << " ";
    preOrder(root->left);
    preOrder(root->right);
}

Main code

int main(){
    vector<int> arr;
    int arr1[8] = {2,9,6,5,7,1,8,4};
    for(auto x:arr1) arr.push_back(x);
    sort(arr.begin(),arr.end());
    
    //Creating a balanced binary tree and inserting elements
    Node* root = sortedArrayToBST(arr, 0 , arr.size()-1);
    cout << "The preorder traversal of tree is:" << endl;
    preOrder(root);
    return 0;
}

Balanced binary tree has the time complexity of O(n) and space complexity of O(n) as well.

Hence, the balanced binary search tree is implemented and can be used wherever needed.