Algorithm behind Bill splitting app

In this article, we have explored the algorithms that are used to design a Bill splitting app. Bill Splitting app is a really simple project idea which is inspired by Splitwise App. So what basically is an Splitwise App?

Splitwise is an App which makes it easy to split bills with friends and family. They organize all your shared expenses in one place so that everyone can see who they owe.

For example, there are group of friends (Yusuf, Harshit, Himanshu, and Yash) and they have made expenses and there are dependencies like Yusuf owes $100 to Harshit, Harshit owes $200 to Himanshu and Yash owes $50 to me. So this is easy for you to split bills in a balanced equation but what if I have a lot of people in my group? It becomes an complex network and you want to make it simpler so that the total number of transactions get minimised and splitting gets easy. Hence Splitwise has a feature of minimising the cash flow between persons.

So lets find out how can we resolve this dependency issue. Which data structure will hit your brain at the first time? Graph, right? Yes!

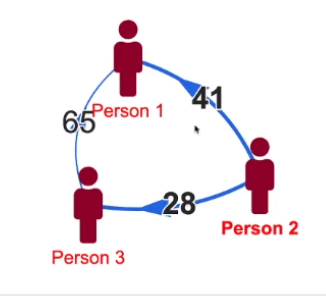
So lets say we have a graph below

This denotes how much money a single person owes to other people in the graph.

So you can see,

• Person_3 owes $65 to Person_1
• Person_2 owes $41 to Person_1 and $28 rupees to Person_3
• And Person_1 owes nobody

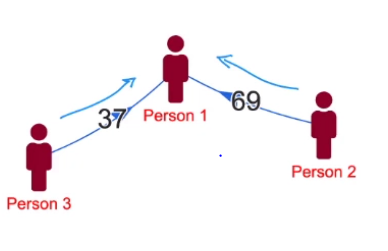
So this can be simplified using the graph algorithm and if you actually see the network gets simplified if Person_3 gives $37 to Person_1 and Person_2 gives $69 to Person_1, refer the below graph.

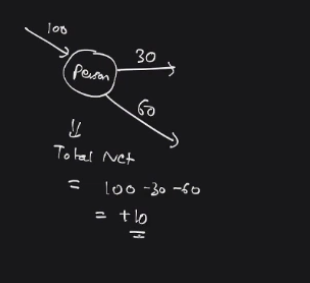
If you want to simplify the transactions for a complex network so you first need to know the Total Net Amount the indiviual person has. Refer the below illustration

In the above illustration, there is a person who has certain debits and certain credits. Suppose he is giving 30 to someone, 60 to someone and taking 100 from someone.
So the Total Net Amount the person has is 100 - 30 - 60 = + 10. So he will actually end up with profit +10.
In the end each person will be either giving money or taking money.

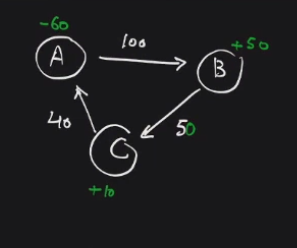
For example, lets try to settle these amounts by taking a list of people who are in debit mode and credit mode for the below graph

So we can observe that B and C are in credit mode and A is in Debit mode. Refer the below image

So the idea is,

1. We can pick the person who has the largest debit and try to settle the person who has the largest credit. So here if A gives 50 to B then the credit of B will become zero and we'll have 1 transaction as of now.
2. This ensures that A will now have 10 and you can see that A is still in the debit mode and from the credit line next person is C(next largest amount).
3. Try to settle these amounts. So we can send 10 to C and A will now have zero amount and C will also be zero.
4. So givers and takers are now having null balance, hence we have successfully balanced the amount and minimum number of transactions happened here is 1 + 1 i.e 2.

So making a Max Heap for a debit and credit list will solve this problem in O(nlog(n)) time complexity.

Another approach: Use multiset data structure.

I would like to thank Prateek Narang for explaining this concept in his course. Also, I would like to thank Aditya from OpenGenus for bringing up this conversation without which I probably wouldn’t have written this blog post.