
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored Art Gallery Problem in depth along with variants of Art Gallery Problem and important results.
Contents
- Introduction to Art Gallery Problem
- Types of Guards
- Exploring a Few Examples
- Solution to the Problem
- Variants of the Art Gallery Problem
- Results
Introduction to Art Gallery Problem
Consider an art gallery which is shaped in the form of a polygon with n vertices. In the art gallery problem, the objective is to find the minimum number of guards that can be placed inside this polygon or on its edges, such that the entire art gallery is visible to this set of guards. The guards cannot move from the vertices at which they are positioned. However, they have a vision of 360°, which means that they can see all around them as long as a wall (an edge of the polygon) does not obstruct their vision. This problem was first presented by Chávtal in 1975.
In geometry, this problem is as follows: Find the minimum number of guards that need to be placed in an n-vertex simple polygon such that all points within the polygon are visible. (A polygon is a closed shape made up of straight lines. A simple polygon refers to a polygon which does not intersect itself, and which does not have any holes.)
Types of Guards
There are multiple types of guards, classified on the basis of the position that they take:
- Vertex Guard: The guard is positioned at the vertex of the polygon.
- Point Guard: The guard is positioned anywhere in the polygon.
- Edge Guard: This guard is placed anywhere along the edges of the polygon.
- Mobile Guard: This guard has the ability to move from one point to another. Although this type of guard is not used in the Art Gallery Problem, they are used in variants of the same.
Exploring a few examples
On examining the problem, it is trivial that in case of a convex polygon (a polygon which has all interior angles less than 180°), only one guard is required, and this guard can be placed in the centre of this polygon. There are multiple other cases where only one guard shall suffice, such as a star.
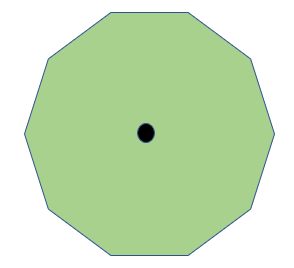
In this example, we can observe that the one guard, (represented by the black dot), will be able to cover the entire polygon.
Now, we observe that more than one guard might be required in case of a non-convex polygon (note that in some non-convex polygons, just one guard will suffice). We show one such example, where two guards are needed.
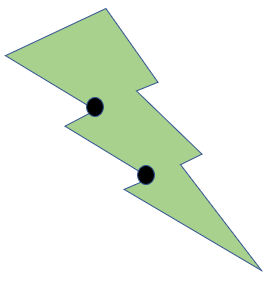
Solution to the problem
The maximum number of guards to guard the art gallery was found to be ⌊n⁄3⌋. This solution was proposed and proved by Chávtal. However, we shall look at a more elegant proof of the same, which was proposed by Steve Fisk. This proof uses triangulation and vertex coloring. We shall describe these in detail.
Theorem Statement
The Art Gallery Theorem is given to be as follows:
⌊n⁄3⌋ guards are occasionally necessary and always sufficient to cover an n - vertex polygon.
To prove this result, we shall first prove a couple of sub-results, which will then be combined to conclude the theorem.
Triangulation always exists for non-convex polygons
Triangulation of a polygon is the process of splitting it into non intersecting triangles by means of lines joining its vertices. We shall now prove that triangulation is possible for a non-convex polygon.
We prove this result using mathematical induction. Consider the base case where n = 3. Here, the result is trivial since the polygon under consideration is already a triangle. Now, assume the result is true up to polygons with n-1 vertices.
Consider a polygon with n sides. Now, we know that the sum of the angles of this polygon is (n-2) x 180°. Hence, the number of angles which are convex would be less than n - 2, since the sum of angles would otherwise be greater than (n - 2) x 180°. Hence, there are at least two convex vertices. Consider the line joining these two vertices. If this line does not lie in the interior of the polygon, then slide one of its endpoints towards the other until it encounters a vertex. Then this line would lie inside the polygon. This particular case is illustrated below:
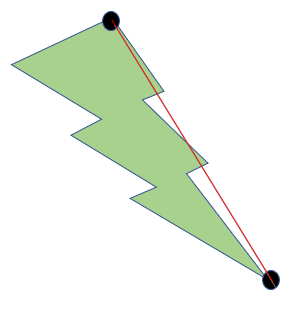
Since the entire line does not lie within the polygon, we slide the line downwards until it lies in the interior of the polygon. Hence, we obtain the following:
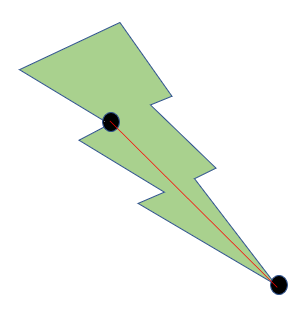
After obtaining such a line, we observe that the line has divided the polygon into two smaller polygons. By hypothesis, triangulation exists for these smaller polygons, and hence exists for the entire polygon. Upon triangulation, the earlier example looks as follows:
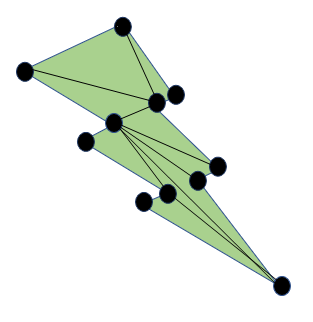
Every non-convex polygon is 3-colorable
A graph is said to be 3-colorable if its vertices can be colored in such a manner that no connected vertices have the same color.
Since triangulation exists for every non-convex polygon. We proceed as follows:
- Consider any two connected vertices, and label them with the first and the second color.
- Now, on each triangle sharing these two vertices, label the third vertex with the third color.
- Continue in this manner by labeling the third vertex with a color different from that of the other two vertices.
After coloring all vertices in this manner, we obtain a 3-colored graph. An example of the three colored graph for the previous example is as follows:
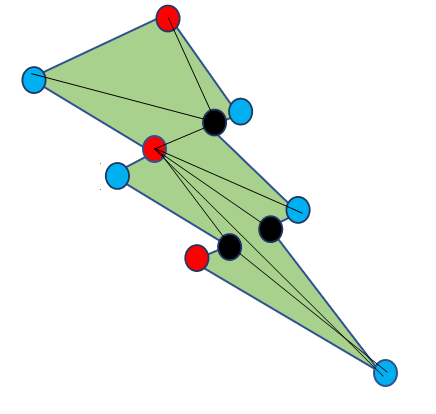
Completing the Proof
On 3-coloring the polygon, we observe that there is at least one color which appears ⌊n⁄3⌋ times. Hence, placing a guard at each of these vertices would mean that each triangle has at least one guard, and thus the entire polygon gets covered.
Therefore, the maximum number of guards to cover the polygon is ⌊n⁄3⌋. Note that this result does not give any information regarding the minimum number of guards.
Variants of the Art Gallery Problem
There are multiple variants of the art gallery problem, most of which have numerous applications. We shall discuss two such variants here:
- Chromatic Art Gallery Problem: Given a polygon, the objective is to find the minimum number of colors such that if the area covered by two guards overlap, then those guards do not have the same color. For this problem we have the following theorem: For every positive integer k, there exists a polygon with 3k2 + 2 vertices such that the minimum number of colors is greater than or equal to k
- The Watchman Route Problem: In this variant, the watchman are not stationary. Instead, the focus is to find the shortest route such that the watchman is able to cover the entire polygon. Two techniques are used to solve this problem: essential cuts and reflection principles. This problem has multiple applications in the field of robotics.
- The Prison Yard Problem, where the guards are standing on the edges such that both the interior and the exterior of the polygon are visible.
Results
Here, we shall take a look at some of the results that were developed for the variants of the art gallery problem.
- O'Ruke proved in 1987 that ⌊(n+2h)⁄3⌋ are sufficient for a polygon with n vertices and h holes. A hole in a polygon is an region within the polygon that does not belong to the polygon. An example of a polygon with a hole is given below:
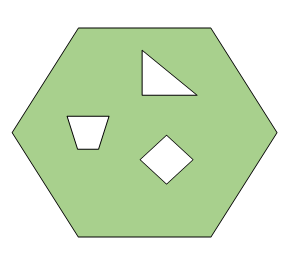
- Kahn, Klawe and Kleitman proved in 1983 that ⌊n⁄4⌋ vertex guards are sufficient for an -vertex orthogonal art gallery. An orthogonal art gallery is one in which all the edges are either along the horizontal x-axis or the vertical y-axis. An example of an orthogonal art gallery is given below:
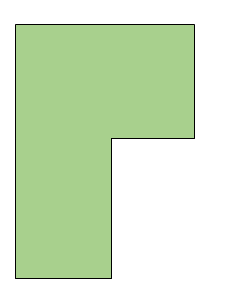
This proof uses the method of convex quadrilateralisation, which is similar to that of triangulation which we followed for the classical art gallery problem.
-
Hoffman and Kriegel proved in 1996 that ⌊n⁄3⌋ are sufficient to guard an orthogonal polygon with n vertices and h holes.
-
O'Rouke proved in 1983 that ⌊n⁄4⌋ mobile guards are sufficient for a simple polygon with n vertices and h holes.
-
Aggarwal proved in 1984 that ⌊(3n +4)⁄16⌋ mobile or edge guards are sufficient to guard an art gallery with n vertices.
-
Gyori et al. proved in 1996 that ⌊(3n+4h+4)⁄16⌋ mobile guards are sufficient for an orthogonal polygon with n vertices and h holes.
With this article at OpenGenus, you must have the complete idea of Art Gallery Problem.
